Предмет и история развития исследования операций
Основные понятия исследования операций
Операция – это любая целенаправленная деятельность по достижению поставленной цели.
Стратегия – это способ действия по достижению поставленной цели.
Показатель эффективности – характеристика эффективности достигнутого результата.
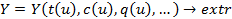 - математическая модель операций.
- математическая модель операций.
У – стратегия, которую мы выбрали.
Критерий эффективности – это набор правил, позволяющих сравнивать между собой эффективности проведенных операций.
ТПР (теория принятия решений)
формализованное неформализованное
(принятие четких решений)
Математические модели
Математическая модель – это упрощенное описание реальности с помощью математических понятий.
Математическая модель - совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.
Можно выделить следующие основныеэтапы построения математической модели:
Ø Определение цели, т.e. чего хотят добиться, решая поставленную задачу.
Ø Определение параметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет.
Ø Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.
Ø Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.
Ø Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом.
Ø Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.e. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.
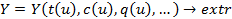 - математическая модель операций.
- математическая модель операций.
У – стратегия, которую мы выбрали.
Критерий эффективности – это набор правил, позволяющих сравнивать между собой эффективности проведенных операций.
Таким образом, оптимальное решение - это решение, предпочтительное перед другими по определенному критерию эффективности (одному или нескольким).
По числу критериев эффективности математические модели делятся наоднокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.
По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.
В стохастических моделях неизвестные факторы - это случайные величины, для которых известны функции распределения и различные статистические характеристики
(математическое ожидание, дисперсия, среднеквадратическое отклонение и т.п.). Среди стохастических характеристик можно выделить:
- модели стохастического программирования, в которых либо в целевую функцию (2.1), либо в ограничения (2.2) входят случайные величины;
- модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент времени является случайной величиной;
- модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований. Также - к стохастическим моделям можно отнести модели теории полезности, поиска и принятия решений.
Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых не определены, используются модели с элементами неопределенности.
В детерминированныхмоделях неизвестные факторы не учитываются. По виду целевой функции и ограничений детерминированные модели делятся на: линейные, нелинейные, динамические и графические.
В линейных моделях целевая функция и ограничения линейны по управляющим переменным.
Hелинейные модели - это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моделей нет единого метода расчета. В зависимости от вида нелинейности, свойств функции и ограничений можно предложить различные способы решения. Однако может случиться и так, что для поставленной нелинейной задачи вообще не существует метода расчета. В этом случае задачу следует упростить, либо сведя ее к известным линейным моделям, либо просто линеаризовав модель.
В динамических моделях учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.
Графические модели - используются тогда, когда задачу удобно представить в виде графической структуры.
Постановка задачи.
Формализация задачи.
Получив достаточно строгую и логически непротиворечивую, содержательную постановку задачи, нужно построить ее математическую модель.
Нахождение метода решения.
Операция
Операция – это любая целенаправленная деятельность по достижению поставленной цели.
Цель – представление о модели будущего результата, способного удовлетворить потребность при имеющихся возможностях.
Выделяют:
1) учебную деятельность;
2) трудовую деятельность;
3) игровую деятельность;
4) отдых.
Отдых — времяпрепровождение, целью которого является восстановление сил, достижение работоспособного состояния организма. Это время, свободное от работы и каких-либо интенсивных занятий.
На достижение цели и реализацию деятельности направлены:
· техническая система;
· человеческая система;
· смешанные системы.
Технические системы создаются людьми. Примеры технических систем: автомобиль, компьютер, система вентиляции.
Человеческая система, связана с управлением.
Смешанные системы: автопилот, завод
Модели и моделирование.
Моделирование – это процесс создания и использования модели.
Модель – это объект по некоторым своим свойствам подобен объекту оригиналу.
Все модели бывают двух типов: материальные и идеальные (знаковые).
В случае, когда моделью является предмет, воспроизводящий те или иные геометрические, физические и т.п. характеристики оригинала. Это - материальное (физическое) моделирование. Исследование таких моделей - реальные эксперименты с ними. Идеальные модели, являются описаниями объектов-оригиналов с помощью схем, графиков, формул, чертежей и т.п.
Математическое моделирование можно разделить нааналитическое, имитационное, комбинированное.
Для аналитическогомоделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических и т.п.) или логических условий.
Имитационноемоделирование — метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Основным преимуществом имитационного моделирования перед аналитическим является возможность решения более сложных задач.
К имитационному моделированию прибегают, когда:
· дорого или невозможно экспериментировать на реальном объекте;
· невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные;
· необходимо сымитировать поведение системы во времени.
Комбинированное (аналитико-имитационное) моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования.
Этапы компьютерного моделирования:
1) выбор объекта моделирования;
2) выбор цели моделирования:
1. оптимизировать…
2. исследовательская (а что будет если…)
3. объяснительные модели (педагогические программные средства);
3) сбор информации;
В ходе сбора информации должна быть обнаружена информационная недостаточность, это значит, что информация есть, но ее недостаточно чтобы однозначно ответить на цели моделирования.
4) огрубление модели (отбор информации);
Необходимо отобрать наиболее существенные факторы и отбросить несущественные по мнению разработчика.
5) построение математической модели;
6) выбор способа решения (аналитический или численный);
7) выбор метода решения;
8) разработка алгоритма решения (при необходимости);
9) написание программы на одном из языков высокого уровня;
10) отладка программы;
11) тестирование программы;
12) компьютерное моделирование или вычислительный эксперимент;
13) анализ полученных результатов.
В ходе анализа нужно дать ответ на вопрос «достигнута ли цель моделирования?»
Симплекс-метод
Пусть дана задача линейного программирования в канонической форме. Т.е. 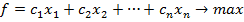
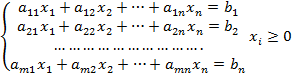
Задачу линейного програмирования записывают в форме модифицированной Жардановой таблице(симплексная таблица)
Для начала необходимо выбрать начальное опорное решение. Для этого Жардановыми исключениями необходимо переменные из заглавной строки перенести в заглавный столбец вместо нулей.
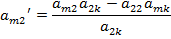
Коэффициенты новой симплексной таблицы находятся по следующему правилу: разрешающий элемент заменяется обратной величиной.
1) Разрешимым называется элемент стоящий на пересечении столбца с переносимой переменной и строки в которую эта переменная переносится.
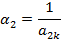
2) остальные элементы разрешающей строки делятся на разрешающий элемент
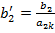 и т.д.
и т.д.
3) Остальные элементы разрешающего столбца делятся на разрешающий элемент и меняют знак на противоположный
4) прочие элементы таблицы вычисляются по правилу прямоугольника
Выполнив достаточное количество Жардановых исключений, исключить все нули в заглавном столбце тогда начальное опорное решение имеет вид: переменные стоящие в заглавном столбце равны свободным членам; переменные оставшиеся в заглавной строке равны 0.
Для того чтобы в столбце свободных членов не появились отрицательные элементы, необходимо придерживаться след. Правилам:
1. Разрешающим может быть выбран любой столбец содержащий хотя бы один положительный элемент.
2. Разрешающий выбирается строка соответствующая минимальному симплексному отношению.
Симплексным отношением называется отношение свободных членов к соответствующим положительным элементам разрешающего столбца.
Замечание.
1. Разрешающие столбцы будут иметь нули в верхней (заглавной) строке и их можно вычеркивать
2. Можно вычеркивать строки из нулей
3. Если в процессе исключений встретится ноль-строка, все элементы которой нули , кроме свободного члена, то система ограничений не имеет решения
4. Если встретится ноль-строка в которой кроме свободного члена других положительных элементов нет, то система не имеет неотрицательных решений
На следующих этапах необходимо проводить оптимизацию найденного опорного начального решения.
Правило оптимизации опорного плана( 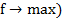
1. Если в f-строке нет отрицательных элементов, кроме свободного члена, то план оптимален
2. Если в f-строке нет также и нулевых элементов, то оптимальный план единственен, если же среди элементов есть хотя бы один нулевой , то оптимальных планов бесконечно много
3. Если в f-строке имеется отрицательный элемент, а в соответствующем ему столбце нет положительных, то целевая функция в допустимой области не ограничена и задача не разрешима.
4. Если в f-строке имеется хотя бы один отрицательный элемент, а в каждом столбце с таким элементом есть хотя бы один положительный, то можно перейти к новому опорному плану более близкому к оптимальному
5. Для наилучшего выбора разрешающего элемента за разрешающий столбец необходимо выбирать столбец с наибольше по модулю отрицательным элементам в f-строке
6. Разрешающей строкой как и раньше выбирается строка с наименьшим симплексным отношением
7. После каждого шага Жардановых исключений найденное решение анализируется на оптимальность.
Симплекс-таблицы
Элементы теории графов.
Теория графов – это раздел дискретной математики, изучающий свойства графов.
Граф – это пара множеств 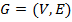 , где V – это подмножество любого счётного множества, а E – подмножество V*V.
, где V – это подмножество любого счётного множества, а E – подмножество V*V.
Маршрутом в графе называется конечная последовательность 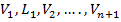 , где
, где 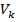 – это вершины,
– это вершины, 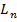 – это ребра, причём ребро
– это ребра, причём ребро 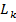 соединяет вершины
соединяет вершины 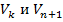 .
.
Граф называется связным, если любые два элемента можно соединить маршрутом.
Маршрут, в котором первая и последняя вершина совпадают, а каждая из остальных встречается ровно один раз, называется циклом.
Связной граф без циклов называется деревом.
Сетевые модели.
Математический аппарат сетевых моделей базируется на теории графов.
Сеть – это ориентированный конечный связной граф, имеющий начальную и конечную вершину. Т.о., сетевая модель представляет собой граф вида «сеть».
Дерево представляет собой связный граф без циклов, имеющий исходную вершину и крайние вершины, а пути от исходной вершины к крайним называются ветвями.
В экономических исследованиях сетевые модели возникают при моделировании экономических процессов методами сетевого планирования и управлениями СПЦ.
Основой сетевого планирования и управления является сетевая модель, в которой моделируется совокупность взаимосвязанных работ и событий, отображающий процесс достижения определённой цели. Она может быть представлена в виде графиков или таблицы.
Основные понятия сетевой модели:
1. событие
2. работа
3. путь
Событие – это результат выполнения одной или нескольких работ. Событие совершается в то момент, когда оканчивается последняя из работ, входящих в него.
Деревья. Остовные деревья
Дерево – это связный ациклический граф.
Дерево – это связный граф без цикла.
Любой граф без цикла называется ….Ребра дерева называются ветвями. Конечные вершины т.е. вершины степени 1называются листья.
Ориентированный граф называется ориентированным деревом если существует ровно одна вершина называемая корнем, которая не имеет предшествующих, и любой вершины несовпадающих с корнем предшествует равно одна вершина.
В произвольном графе G=(V,E) можно выделить подграф G,т.е. G’=(V,E’), E’ с E, который является деревом это дерево называется стягивающим или оставным.
Ребра которые не вошли в дерево называются хордами.
Теорема. Число деревьев в связном графе равно алгебраическому дополнению любого элемента матрицы Кегрофа
Основные понятия исследования операций
Операция – это любая целенаправленная деятельность по достижению поставленной цели.
Стратегия – это способ действия по достижению поставленной цели.
Показатель эффективности – характеристика эффективности достигнутого результата.
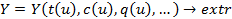 - математическая модель операций.
- математическая модель операций.
У – стратегия, которую мы выбрали.
Критерий эффективности – это набор правил, позволяющих сравнивать между собой эффективности проведенных операций.
ТПР (теория принятия решений)
формализованное неформализованное
(принятие четких решений)
Математические модели
Математическая модель – это упрощенное описание реальности с помощью математических понятий.
Математическая модель - совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.
Можно выделить следующие основныеэтапы построения математической модели:
Ø Определение цели, т.e. чего хотят добиться, решая поставленную задачу.
Ø Определение параметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет.
Ø Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.
Ø Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.
Ø Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом.
Ø Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.e. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.
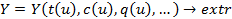 - математическая модель операций.
- математическая модель операций.
У – стратегия, которую мы выбрали.
Критерий эффективности – это набор правил, позволяющих сравнивать между собой эффективности проведенных операций.
Таким образом, оптимальное решение - это решение, предпочтительное перед другими по определенному критерию эффективности (одному или нескольким).
По числу критериев эффективности математические модели делятся наоднокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.
По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.
В стохастических моделях неизвестные факторы - это случайные величины, для которых известны функции распределения и различные статистические характеристики
(математическое ожидание, дисперсия, среднеквадратическое отклонение и т.п.). Среди стохастических характеристик можно выделить:
- модели стохастического программирования, в которых либо в целевую функцию (2.1), либо в ограничения (2.2) входят случайные величины;
- модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент времени является случайной величиной;
- модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований. Также - к стохастическим моделям можно отнести модели теории полезности, поиска и принятия решений.
Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых не определены, используются модели с элементами неопределенности.
В детерминированныхмоделях неизвестные факторы не учитываются. По виду целевой функции и ограничений детерминированные модели делятся на: линейные, нелинейные, динамические и графические.
В линейных моделях целевая функция и ограничения линейны по управляющим переменным.
Hелинейные модели - это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моделей нет единого метода расчета. В зависимости от вида нелинейности, свойств функции и ограничений можно предложить различные способы решения. Однако может случиться и так, что для поставленной нелинейной задачи вообще не существует метода расчета. В этом случае задачу следует упростить, либо сведя ее к известным линейным моделям, либо просто линеаризовав модель.
В динамических моделях учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.
Графические модели - используются тогда, когда задачу удобно представить в виде графической структуры.
Предмет и история развития исследования операций
Корни исследования операций уходят в далекую историю. Резкое увеличение размеров производства, разделение труда обусловило постепенную дифференциацию управленческого труда. Появилась необходимость в планировании материальных, трудовых и денежных ресурсов, в учете и анализе труда и выработке прогноза на будущее. В управленческом аппарате начали выделяться подразделения: отдел финансов, сбыта, бухгалтерии, планово экономический отдел и другие, принявшие на себя отдельные управленческие функции.
К этому периоду относятся первые работы по исследованию в области организации труда и управления - первые предвестники будущей науки.
Как самостоятельное научное направление исследование операций оформилось в начале 40-х годов.
Первые публикации по исследованию операций относятся к 1939-1940 гг, в которых методы применены для решения военных задач, в частности для анализа и исследования военных операций. Отсюда и пошло название дисциплины.Позднее принципы и методы исследования операций стали применяться в сфере промышленно финансового управления. С увеличением масштабов производства расширялись масштабы операционных исследований, круг решаемых задач, совершенствовались методы новой науки.
В 1957 г. была создана Международная федерация исследования операций IFORS , в состав которой входили национальные общества и комитеты по исследованию операций многих стран.
Исследование операций — дисциплина, занимающаяся разработкой и применением методов нахождения оптимальных решений на основе математического моделирования, статистического моделирования и различных эвристических подходов в различных областях человеческой деятельности.
Предмет исследования операций - системы организационного управления или организации, которые состоят из большого числа взаимодействующих между собой подразделений не всегда согласующихся между собой и могут быть противоположны.
Цель исследования операций - количественное обоснование принимаемых решений по управлению организациями.
Основные этапы исследования операций:
Постановка задачи.
Формализация задачи.
Получив достаточно строгую и логически непротиворечивую, содержательную постановку задачи, нужно построить ее математическую модель.
Нахождение метода решения.
