Fzero('функция',x) возвращает уточненное значение x, при котором достигается нуль функции, представленной строкой,при начальном значении аргумента x. (функция в нуле меняет знак)
Если такая точка не найдена то выдается NaN
(Not-a-Number не числовой характер данных)
x1=fzero('x-5',4)
x2=fzero('x-5',2)
x3=fzero('2^x-8',0)
x4=fzero('2^x-7',0)
x5=fzero('0.25*x+sin(x)-1',5)
>> x1=fzero('x-5',4)
x1 =
>> x2=fzero('x-5',2)
x2 =
>> x5=fzero('0.25*x+sin(x)-1',5)
x5 =
5.8128
Для более сложных функций: сначала построим график функции
для приближенного определения корней и интервалов.
Пример 1
Найдем нули функции y=x.^3-9*x.^2+26.*x-24;
x=1.5:0.5:4.5;
y=x.^3-9*x.^2+26.*x-24;
Постройте график, проанализируйте его и при необходимости
Измените интервал для Х и шаг так, чтобы хорошо были видны корни.
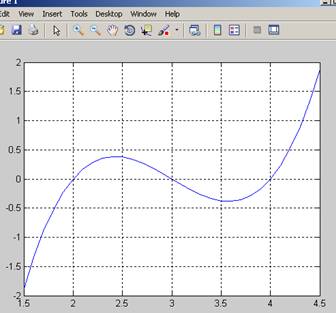
plot(x,y),grid %добавим сетку
теперь уточним значение корней в окрестности точек, где функция y=x.^3-9*x.^2+26.*x-24; пересекает ось ОХ.
x1=fzero('x^3-9*x^2+26*x-24',1.8)
x2=fzero('x^3-9*x^2+26*x-24',3.1)
x3=fzero('x^3-9*x^2+26*x-24',4.3)
%Правильный ответ должен быть 2, 3, 4.
>> x=1.5:0.1:4.5;
>>
>> y=x.^3-9*x.^2+26.*x-24;
>> plot(x,y),grid
Уточним значение корней 1.8 3.1 4.3
 |
>> x1=fzero('x^3-9*x^2+26*x-24',1.8)
x2=fzero('x^3-9*x^2+26*x-24',3.1)
x3=fzero('x^3-9*x^2+26*x-24',4.3)
x1 =
x2 =
3.0000
x3 =
--------------------------------------------
Пример 2
Найдем нули функции
Y=x.^2-5*x+6
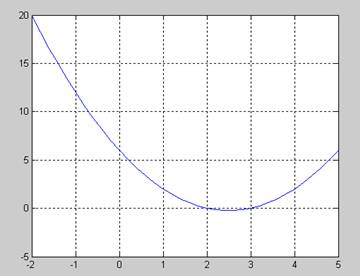
Построим график
x=-2:0.2:5;
plot(x,x.^2-5*x+6)
grid on;
x=fzero('x^2-5*x+6',1)
x=fzero('x^2-5*x+6',4)
%Правильный ответ должен быть 2, 3.
 |
x=fzero('x^2-5*x+6',1)
x=fzero('x^2-5*x+6',4)
x =
x =
3.0000
2)Вычисление нулей функции на интервале:
%-------------fzero('функция',[x1,x2])------------
Для Примера 1
x1_1=fzero('x^3-9*x^2+26*x-24',[1.8 4.5])%возвращает только один корень т.к. fzero('функция',[x1,x2])работает только с интервалом с одной сменой знака.
x1_1=fzero('x^3-9*x^2+26*x-24',[1.8 2.3])(x1_1 = 2.0000 )
--------------------------------------------------------------------------------
Пример 3
Найдем нули функции Y=cos(x);
x=-2*pi:0.1:2*pi;
Plot(x,cos(x))
x=fzero('cos',[1 3])
или x=fzero('cos(x)',[1 3])
или х= fzero(@cos.[1 3])
нельзя написать интервал 'cos',[-5 5], т.к. на этом интервале много смен знаков - выдает ошибку.
На интервале [1 3] только одна смена знака
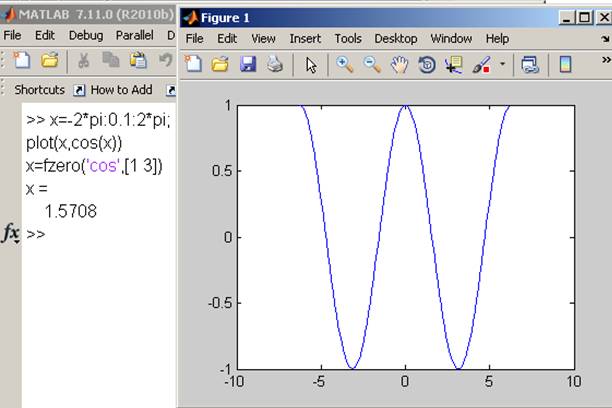 |
корень = 1.57
Пример 4
Найдем нули функции 0.25*x+sin(x)-1;
сначала построим график функции для приближенного определения корней и интервалов
x=0:0.1:10;
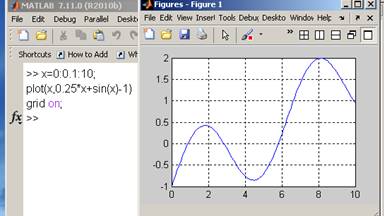
plot(x,0.25*x+sin(x)-1)
grid on; %по графику видно, что нули функции нужно искать в интервалах %[0.5 1], [2 3], [5 6]
x1=fzero('0.25*x+sin(x)-1',[0.5 1])
x2=fzero('0.25*x+sin(x)-1',[2 3])
x3=fzero('0.25*x+sin(x)-1',[5 6])
 |
x1 =
0.8905
x2 =
2.8500
x3 =
5.8128
3)Вычисление нулей функции с заданной точностью:
--------------fzero('функция',x,eps) --------
Для Примера 4
x4=fzero('0.25*x+sin(x)-1',5,0.00001)
x4=fzero('0.25*x+sin(x)-1',[5 6],0.00001)
-------------------------------------------------------------
4)Вычисление нулей функции с п\п функцией
Функцию y=0.25*x+sin(x)-1 мы оформили как М-функцию fun5.m и сохранили в отдельном файле с именем fun5.m в той же директории, что и вызывающая её программа.
Под функциями понимаются как встроенные функции, например sin(x) или ехр(х),так и функции пользователя, например f(x), задаваемые как M-файлы-функции. Например, функция fe=@exp; сохранена как M-файл.
function f=fun5(x);функция; fun5 – имя функции
f=0.25*x+sin(x)-1;
x1=fzero('fun5',[0.5 1])на интервале
>> x1=fzero('fun5',[0.5 1])
x1 =
0.8905
Или
для функции вместо апострофов ставим собаку @
x2=fzero(@fun5,[2 3])на интервале
>> x2=fzero(@fun5,[2 3])
x2 =
2.8500
x3=fzero('fun5',6)в окрестности точки
>> x3=fzero('fun5',6)
x3 =
5.8128
Функция roots
Вычисление корней полинома
Пример 1
Найдем нули (корни) функции y=x2-5x+6
y=[1 -5 6]; %матрица коэффициентов полинома x2-5x+6=0
x=roots(y);
Vpa(x,2)
ans =
3.0
2.0
Пример 2
Полином x3-9*x2+26*x-24=0
y=[1 -9 26 -24]; %матрица коэффициентов
x=roots(y);
Vpa(x,2)
%ответ: 4 3 2
Пример 3
Найти корни полинома 2х4 - 8х3 + 8х2 - 1
disp('корни полинома 2х^4 - 8х^3 + 8х^2 - 1')%печатает комм.
%без графика:
p=[2 -8 8 0 -1];
Roots(p)
%Ответ 2.3066; 1.5412; 0.4588; -0.3066
с графиком:
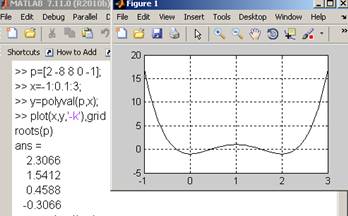
p=[2 -8 8 0 -1];p-вектор, элементы которого являются коэффициентами полинома
x=-1:0.1:3;в порядке уменьшения степеней, X может быть матрицей или вектором
y=polyval(p,x); возвращает значения полинома в точках, заданных в массиве Х
Plot(x,y,'-k'),grid
roots(p)%Ответ 2.3066; 1.5412; 0.4588; -0.3066
 |
___________________________________________________
Функция solve
