Математическое моделирование с использованием Excel

Цель работы:

- научиться использовать электронные таблицы для выбора оптимального решения поставленной задачи и проверки правильности построения математической модели.

ЗАДАЧА № 1. Получить аналитическое выражение, описывающее динамику численности населения России на основе имеющихся статистических данных. В качестве аппроксимирующей функции выбрать уравнение .

Методические указания

ЗАДАНИЕ 1. Заполните таблицу (табл. 9.1).

Таблица 9.1.

Таблица эксперимента
a	b	Год	Численность статистич.	Численность теоретич.	Отклонение
			117,5
			130,1
			137,6
			147,4
			148,5
			147,7
			148,7
			148,4
			148,3
				Погрешность

1.1. Сделайте заголовок и заполните шапку таблицы.

1.2. Столбцы А и В отведите под коэффициенты а и b соответственно.

1.3.В столбец С занесите значения лет начиная с 1960 г. (см. табл. 9.1.).

1.4. В столбец D занесите взятые из справочника значения численности населения России с 1960 г. в млн.чел. (см. табл. 9.1.).

ЗАДАНИЕ 2. Подберите значения коэффициентов а и b.

2.1. Постройте график типа X-Y (Точечная) по данным таблицы. (X - годы; Y - статистическая численность).

2.2. Перемасштабируйте оси Х и Y для более наглядного представления данных.

§ Выделите ось X.

§ Вызовите контекстно-зависимое меню и выполните команду: Форматировать ось, Шкала.

§ Установите минимальное значение X, основную единицу измерений и пересечение с осью У.

§ Аналогично перемасштабируйте ось Y.

2.3. Аппроксимируйте полученную прямую.

Необходимо статические данные по численности населения представить на графике плавной кривой (аппроксимировать). Эта кривая называется линией тренда. Для построения линии тренда:

§ Выделите линию графика.

§ Выполните команду Добавить линию тренда из контекстно-зависимого меню. Откроется диалоговое окноЛиния тренда.

§ Выберите Экспоненциальный тип ( ).

§ Выберите в диалоге Линия тренда вкладку Параметр.

§ Установите флажок [Ö] Показывать уравнение на диаграмме и нажмите кнопку ОК.

В результате на графике появится линия тренда и уравнение с подобранными коэффициентами а и b (рис. 9.1).

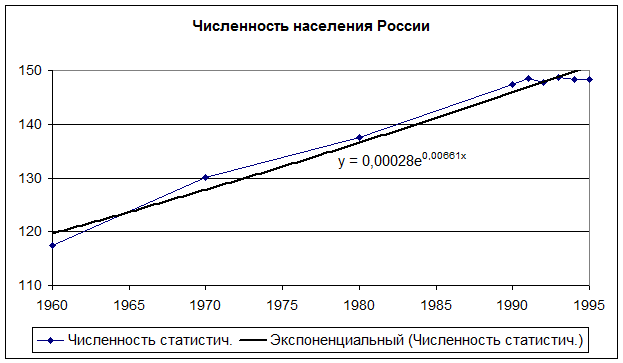
Рис. 9.1.

2.4. Занесите полученные значения коэффициентов а и b в ячейки A3 и ВЗ и присвойте им имена: A3 - имя а, В3 - имя b.

Коэффициенты а и b не изменяются с течением времени, это константы, следовательно, при вычислении теоретической численности они должны быть адресованы абсолютно.

ЗАДАНИЕ 3. Вычислите теоретическую численность по формуле .

3.1. В ячейку ЕЗ занесите формулу =а*ЕХР(b*СЗ)

3.2. Скопируйте формулу в ячейки Е4:Е11.

ЗАДАНИЕ 4. Вычислите отклонения и погрешность найденной аппроксимации.

Отклонение - это модуль разности теоретических и фактических значений функции у. Погрешность - это максимальное отклонение.

4.1. В ячейку F3 занесите формулу =ABS(E3-D3).

4.2. Скопируйте формулу в ячейки F4:F11.

4.3. В ячейку F13 введите функцию определения максимального из чисел этого столбца.

ЗАДАНИЕ 6. Подберите значения коэффициентов а и b более точно.

При полученных в результате аппроксимации коэффициентах а и b погрешность уже не плохая (по условию она должна быть в пределах нескольких миллионов). Но коэффициенты а и b можно подобрать более тонко, используя функцию Поиск решения. В отличие от Подбора Параметра Поиск решения может для достижения нужного результата изменять или подбирать подходящие значения во многих ячейках.

6.1. Выполните команду: Сервис, Поиск Решения. (При отсутствии в меню Сервис функции Поиск решения выполните следующие действия: Сервис, надстройки. Откроется окно, в котором необходимо установить флажок [Ö] Поиск решения.)

6.2. Сделайте необходимые надстройки в окне диалога Поиск решения.

6.3. В поле Установить целевую ячейку укажите адрес ячейки $F$13 (в ней погрешность).

6.4. Установите переключатель [·] минимальному значению.

6.5. В поле Изменяя ячейки укажите $А$3:$В$3.

В этом поле задаются адреса ячеек, значения которых будут варьироваться в процессе поиска решения. В нашем случае - это адреса ячеек со значениями а и b.

6.6. Нажмите на кнопку Выполнить.

Начнется поиск решения. Так как у нас довольно точные коэффициенты а и b, то поиск займет немного времени. Когда Excel найдет решение, то откроется диалог, предлагающий Сохранить найденное решение.

6.7. Нажмите кнопку ОК.

Произойдет изменение значений ячеек в соответствии с найденным решением. Обратите внимание, что коэффициенты а и b изменились, а погрешность уменьшилась.

ЗАДАНИЕ 7. Определите численность населения в России в 2000 г.

7.1. Подставьте в ячейку С12 число 2000.

7.2. В Е12 скопируйте формулу из E11.

В ячейке Е12 появится искомое число.

ЗАДАНИЕ 8. Постройте на одной диаграмме совмещенные графики роста численности населения ни основе статистических и теоретических данных.

8.1. Выделите на построенном графике линию тренда и удалите ее, выполнив команду Очиститьв контекстно-зависимом меню линии тренда.

8.2. Добавьте в уже построенную диаграмму теоретические данные.

• В таблице эксперимента выделите теоретические данные Е2:Е12.

• Установите указатель мыши на правой границе выделенного блока.

• Нажмите левую кнопку мыши и пробуксируйте данные на диаграмму.

• В появившемся окне сделайте настройку (если это необходимо).

8.3. Оформите диаграмму в соответствии с рис. 9.2, где показан примерный вид графиков.

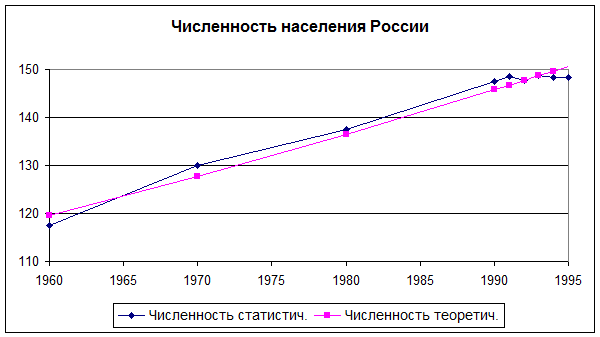
рис. 9.2.

ЗАДАНИЕ 9. Оформите таблицу на свой вкус (граница, фон, шрифты).

ЗАДАНИЕ 10. Воспользуйтесь предварительным просмотром печати

10.1. Разместите диаграмму на одном листе с таблицей.

10.2. Добейтесь хорошего расположения таблицы и диаграммы на листе.

10.3. Установите верхний колонтитул: Численное моделирование. Работу выполнил <Фамилия и Имя>. В нижнем колонтитуле укажите дату и время.

ЗАДАНИЕ 11. Сохраните файл под именем lab9_1.xls.

ЗАДАНИЕ 12. Проанализировав данные таблицы и графики, сделайте вывод об адекватности предложенной математической модели реальному процессу (т.е. вывод о правильности описания роста населения формулой ).

ЗАДАЧА №2

Методические указания

ЗАДАНИЕ 1. Заполните таблицу эксперимента (табл. 9.2).

Таблица 9.2.

Таблица эксперимента
a	b	Входная плата х	Среднее кол-во посетителей эксперим. Р(х)	Выручка эксперим.	Среднее кол-во посетителей теоретич. Р(х)	Выручка теоретич.	Отклонение
		1,5	17,5
		2,0	16,0
		2,5	14,0
		3,0	12,5
		3,5	11,0
		4,0	9,2
		5,0	7,0
					Погрешность:

1.1. Сделайте заголовок и заполните шапку таблицы.

1.2. Столбцы А и В отведите под коэффициенты а и b соответственно.

1.3. В столбец С занесите данные по входной плате (табл. 9.2).

1.4. В столбец D занесите экспериментальные данные по среднему числу посетителей (см. табл. 9.2).

1.5. В столбце Е подсчитайте выручку на основе экспериментальных данных как произведение входной платы на количество посетителей.

ЗАДАНИЕ 2. Подберите приближенные значения коэффициентов а и b.

Подбор коэффициентов а и b выполняется аппроксимацией экспериментальных данных по аналогии с задачей 1.

2.1. Постройте диаграмму типа X-Y по экспериментальным данным. (Х – входная плата, Y - экспериментальные данные по количеству посетителей).

2.2. Аппроксимируйте полученную кривую.

При построении линии тренда следует выбрать полиномиальный тип ( 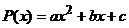) и указать Y-пересечение = 24.

2.3. Занесите полученные значения коэффициентов а и b в таблицу.

ЗАДАНИЕ 3. Вычислите теоретическое количество посетителей и теоретическую выручку.

3.1. В столбце F вычислите по формуле 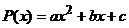теоретическое количество посетителей, причем, как объяснялось выше, с=24.

3.2. В столбце G вычислите теоретическую выручку.

ЗАДАНИЕ 4. Вычислите отклонение между экспериментальной и теоретической выручкой и погрешность (аналогично заданию 4 в задаче 1).

4.1. В столбце Н вычислите отклонение между экспериментальной и теоретической выручкой.

4.2. В свободной ячейке столбца Н определите погрешность.

ЗАДАНИЕ 5. Подберите коэффициенты а и b, стараясь минимизировать погрешность (аналогично заданию 5 в задаче 1).

ЗАДАНИЕ 6. Постройте графики.

6.1. Постройте на одной диаграмме два графика типа X-Y (экспериментальный и теоретический) зависимости количества посетителей от входной платы P=f(x) (аналогично заданию 8 в задаче 1). Разместите диаграмму на одном листе с таблицей.

6.2. Постройте на одной диаграмме два графика типа X-Y (экспериментальный и теоретический) зависимости выручки от входной платы х. Разместите диаграмму на том же листе.

ЗАДАНИЕ 7. Определите, при какой входной плате выручка будет максимальна. Каково среднее количество посетителей сеанса при найденной оптимальной входной плате?

ЗАДАНИЕ 8. Оформите таблицу на свой вкус (обрамление, заполнение, шрифты).

ЗАДАНИЕ 9. Воспользуйтесь предварительным просмотром печати.

9.1. Добейтесь хорошего расположения таблицы и двух диаграмм на листе.

9.2. Установите верхний колонтитул: Численное моделирование. Работу выполнил <Фамилия и Имя>. В нижнем колонтитуле укажите дату и время.

ЗАДАНИЕ 10. Сохраните файл в личном каталоге под именем lab9_2.xls.

ЗАДАНИЕ 11. Проанализировав данные таблицы эксперимента и графики, сделайте вывод об адекватности предложенной математической модели.