Равномерная и неравномерная сходимость

По определению предела числовой последовательности ряд

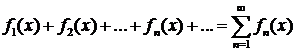сходится в данной области, если, как бы мало ни было число 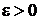, можно указать такое целое число N, что при всех 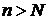выполняется неравенство 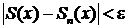. В этом случае для функциональных рядов могут представляться два случая:

1. Можно найти число N, общее для всех значений х, входящих в область сходимости ряда, в этом случае записанный выше ряд называется равномерно сходящимся в данной области.

2. Такого общего числа N для всех х, лежащих в области сходимости, нет: каково бы ни было n, найдется в области сходимости такое число х, что 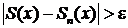. В этом случае в данной области ряд сходится неравномерно.

Признак (Вейерштрасса) равномерной сходимости ряда

Ряд 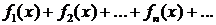равномерно сходится в данной области, если существует такой сходящийся числовой ряд 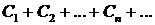положительных членов, что для всех значений х, лежащих в этой области, имеет место неравенство: 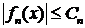. В этом случае числовой ряд 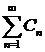называется можорантой функционального ряда .

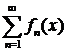Пример. Ряд 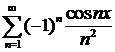– равномерно сходящийся в любой области,
т. к. числовой ряд 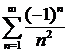– абсолютно сходящийся и .

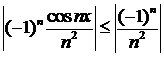(Числовой ряд 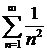– сходящийся ряд Дирихле).

Ряды Тейлора

12.5.1. НЕОБХОДИМОЕ УСЛОВИЕ РАЗЛОЖЕНИЯ ФУНКЦИИ
В РЯД ТЕЙЛОРА

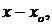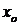(по степеням где – фиксированная точка). Если непрерывная функция 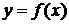бесконечное число раз дифференцируема в окрестности точки 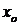, то она может быть представлена в виде ряда Тейлора:

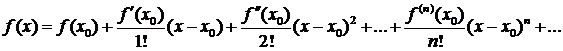
12.5.2. ДОСТАТОЧНОЕ УСЛОВИЕ РАЗЛОЖЕНИЯ ФУНКЦИИ
В РЯД ТЕЙЛОРА

называется достаточным условием сходимости ряда Тейлора к порождающей его функции и заключается в следующем. Чтобы ряд Тейлора сходился к порождающей его функции 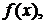т. е. сумма ряда Тейлора совпадала с данной функцией: 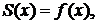достаточно, чтобы 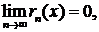где остаточный член 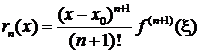и 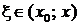(форма Лагранжа).

Пример. Разложить в ряд Тейлора функцию 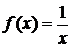по степеням .

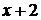Решение. Запишем ряд Тейлора для данной функции при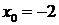

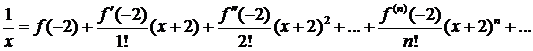
и вычислим значения данной функции и ее производных в точке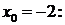

……………….. ……………….

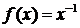
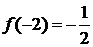
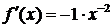
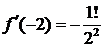
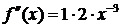
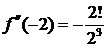
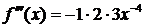
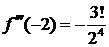
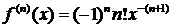
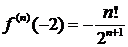
Найденные значения подставим в ряд Тейлора и получим разложение данной функции по степеням :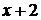

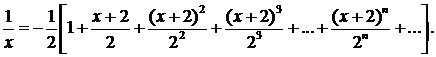
Исследуем сходимость этого ряда по признаку Даламбера:

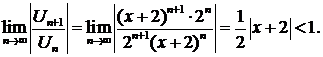
Решая последнее неравенство, находим интервал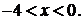

Границы этого интервала исследуем особо.

Подставляя в ряд 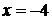, затем 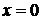, получим числовые ряды 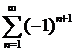и 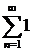, которые расходятся, так как для каждого из этих рядов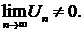

Следовательно, интервал сходимости полученного ряда Тейлора для функции 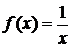есть промежуток .

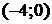Замечание. Исследуя остаточный член 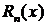формулы Тейлора, можно убедиться, что полученный ряд сходится к данной функции именно на указанном интервале.

РЯД МАКЛОРЕНА

Если 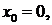то ряд Тейлора называется рядом Маклорена и разложение функции 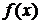в ряд Маклорена называется разложением функции по степеням х и имеет следующий вид:

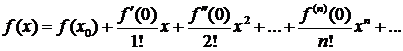
Замечание. Значение функции 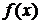и суммы ряда совпадают лишь в точках области сходимости.