Свойства простейших векторных полей

1) Векторное поле а, для всех точек которого дивергенция равна нулю 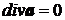, называется трубчатым или соленоидальным.

2) Если во всех точках поля а ротор равен нулю: 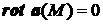, то поле называется безвихревым или потенциальным.

3) Векторное поле а, являющееся одновременно и потенциальным ( 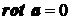) и соленоидальным ( 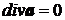), называется гармоническим.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Основные понятия

● Уравнение, связывающее независимую переменную х, искомую функцию и ее производные, называется дифференциальным. Порядком дифференциального уравнения называется наивысший из порядков входящих в это уравнение производных искомой функции. Например, уравнения и – первого порядка; уравнения и – второго порядка; уравнение – четвертого порядка. Общий вид уравнения n-го порядка

(1)

В частности, это уравнение, разрешенное относительно старшей производной, примет вид

(2)

● Решением дифференциального уравнения называется функция , которая после подстановки ее и ее производных превращает уравнение в тождество. График решения дифференциального уравнения называется интегральной кривой.

● Задача Коши: найти решение уравнения (2), удовлетворяющее условиям …, (начальные условия).

Можно показать, что при определенных требованиях к правой части уравнения (2) данная задача (задача Коши) имеет единственное решение. Рассмотрим эти требования, например, для дифференциального уравнения первого порядка (3)

Теорема Коши (существования и единственности решения). Если правая часть уравнения (3) и ее частная производная определены и непрерывны в некоторой области D изменения переменных х и у, то, какова бы ни была внутренняя точка этой области, данное уравнение имеет единственное решение , которое при принимает заданное значение .

Геометрический смысл теоремы Коши следующий: через каждую внутреннюю точку области D проходит единственная интегральная кривая.

Дадим теперь определение общего и частного решений дифференциального уравнения (3), правая часть которого удовлетворяет в некоторой области D условиям теоремы Коши.

● Функция , зависящая от аргумента х и произвольной постоянной С, называется общим решением уравнения (3) в области D, если она удовлетворяет двум условиям:

1) при любых значениях произвольной постоянной С, принадлежащих некоторому множеству, функция является решением уравнения (3);

2) какова бы ни была точка , лежащая внутри области D, существует единственное значение постоянной такое, что решение удовлетворяет начальному условию: .

Всякое решение уравнения (3), получающееся из общего решения при конкретном значении , называется частным решением.

Если общее решение дифференциального уравнения найдено в виде, не разрешенном относительно у, т. е. в виде , то оно называется общим интегралом уравнения.