Тогда в некоторой точке отрезка функции обращается в ноль.
То есть,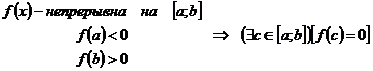 
Пусть функция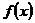 
непрерывна на своей области определения, 
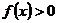. Для применения метода интервалов нужно найти область определения функции, а затем решить уравнение 
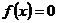и найти его корни. Эти точки разбивают область определения функции на интервалы, на каждом из которых функция сохраняет свой знак. На каждом таком интервале функция сохраняет знак именно по теореме Больцано-Коши, так как если предположить, что хотя бы в одной точке внутри одного из таких интервалов функция меняет свой знак, то значит, что существует еще одна точка, в которой функция обращается в ноль. Но все нули функции - корни уравнения 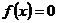, которые являются концами интервалов и никаких других нулей у функции быть не может.
Знак функции на каждом таком интервале можно определить по одной точке, а для рациональной функции можно использовать чередование знаков с учетом степени сомножителей. Если степень сомножителя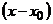 
четная, то при переходе через точку 
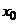знак функции не меняется, если степень сомножителя 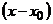нечетная, то при переходе через точку 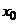знак функции меняется.
Приведем алгоритм применения метода интервалов:
1) Приведем неравенство к виду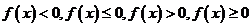 
. Для этого переносим все члены в левую часть.
2) Приводим все члены в левой части к общему знаменателю.
3) Числитель и знаменатель полученной дроби раскладываем на сомножители. Сомножители должны быть либо линейные (т. е. вида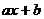 
), либо квадратные трехчлены, не имеющие действительных корней, т. е. не раскладывающиеся на линейные сомножители. Если в числителе и в знаменателе есть общие сомножители, то сокращать их пока не будем.
4) Отметим нули числителя и знаменателя на числовой прямой. Нули знаменателя отмечаем всегда «выколотыми» точками, а нули числителя «выколотыми» точками, если неравенство строгое, и «закрашенными», если неравенство нестрогое. После этого общие сомножители в числителе и в знаменателе нужно сократить.
5) Полученные точки разбивают числовую прямую на промежутки, на которых левая часть сохраняет свой знак (По теореме Больцано-Коши). Нам нужно только определить знак на каждом промежутке.
Первый способ: нужно взять по одной точке из каждого промежутка (обязательно внутри, а не на конце) и вычислить в этих точках значения левой части.
Второй способ: заметим, что сомножитель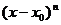 
в нечетной степени меняет знак «при переходе через точку 
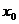», а сомножитель четной степени не меняет знака. Можно определить знак на самом правом промежутке, а затем расставить знаки, учитывая переходы через все нули. Остается только выбрать промежутки с нужным знаком.
Пример.
Решить неравенство 
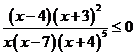
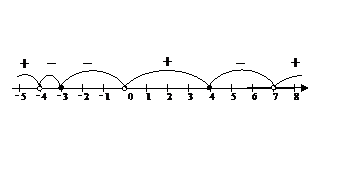
Отметим нули числителя и знаменателя на числовой прямой, вычислим знак левой части на каждом из получившихся промежутков.
Выберем те промежутки, на которых функция имеет нужный знак.
Ответ: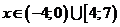 
21. Формулы приведения.
Тригонометрические функции углов вида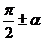 
, 
, 
, 
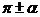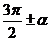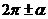могут быть выражены через функции угла 
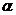с помощью формул, которые называются формулами приведения.
Формулы приведения предназначены для того, чтобы выражать значения тригонометрических функций произвольных углов через функции острого угла.
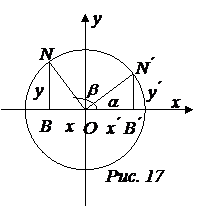Все приводимые ниже формулы справедливы при произвольных значениях угла 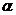(естественно, входящих в область определения соответствующих функций), хотя применяются преимущественно в тех случаях, когда угол 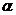– острый.
Докажем сначала, что для любого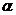
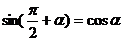и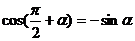 
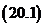
Для определённости предположим, что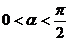 
. Тогда для угла 
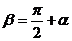справедливо двойное неравенство 
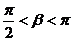. Рассмотрим радиусы 
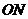и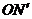 
, образующие углы 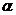и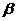 
с положительным направлением оси 
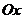соответственно (рис. 17). Опустим из точек 
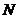и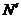 
перпендикуляры на ось 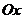. Полученные треугольник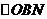и 
и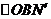 
равны, поскольку они прямоугольные, 
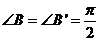, имеют равные гипотенузы ( 
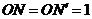) и равные острые углы: 
.
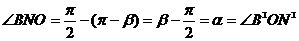Из равенства треугольников следует, что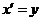 
и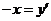 
. Следовательно, 
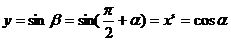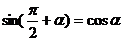, . Вторая формула получается с помощью аналогичных рассуждений.
Для тангенса и котангенса формулы приведения следуют из равенств
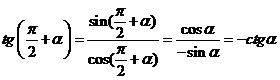и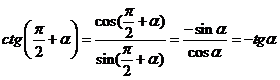 
.
Из формул 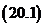, а также с учётом чётности и нечётности тригонометрических функций можно получить формулы
, 
, 
, 
. 
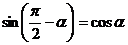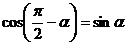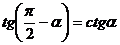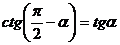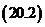
Например,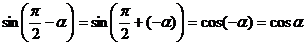 
.
Формулы приведения для синуса и косинуса угла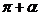 
выглядят так:
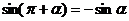и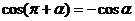 
. 
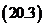
Для доказательства достаточно представить 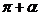в виде 
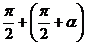и дважды воспользоваться формулами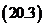 
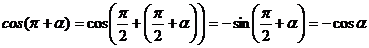. Аналогичные формулы для тангенса и котангенса 
, 
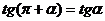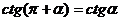можно получить с помощью формул приведения для синуса и косинуса.
Из формул (3) следует:
, 
, 
, 
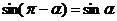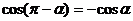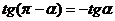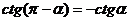. (20.4)
Для доказательства достаточно представить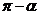 
в виде суммы 
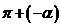и применить формулы (20.3).
Формулы приведения для углов 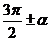имеют вид
, 
, 
, 
.
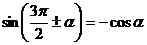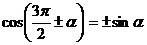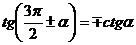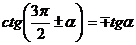Для доказательства этих формул надо представить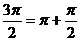 
и последовательно применить формулы (20.3) и (20.1).
Справедливы также формулы
, 
, 
, 
.
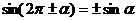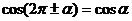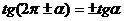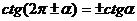Перечисленные выше формулы могут быть обобщены одним правилом:
Любая тригонометрическая функция 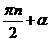угла 
по абсолютной величине равна той же функции угла 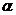, если число n - чётное, и ко-функции этого же угла, еслиn – нечётное.
При этом если функция угла 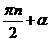положительна, когда 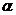– острый положительный угол, то знаки обеих функций одинаковы; если отрицательна, то различны.
22. Зависимости между тригонометрическими функциями одного и того же аргумента