Гипотезы об однородности выборок – это гипотезы о том, что рассматриваемые выборки извлечены из
одной и той же генеральной совокупности
Дан вариационный ряд выборкиn= 7: –5, –4, 0, 1, 2, 3, 3. Для этого ряда:
выборочная медианаd= 1, выборочное среднее 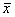 = 0
= 0
Дан вариационный ряд выборкиn= 8: –3, –1, 0, 2, 4, 6, 7, 8. Медиана этого рядаd= ______ (наберите число).
Дан вариационный ряд выборкиn= 8: -3, -2, 0, 0, 2, 3, 4, 4. Для этого ряда:
выборочная медианаd= 1, выборочное среднее 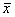 = 1
= 1
Дан вариационный ряд выборкиn= 8: -5, -4,-1, 0, 2, 2, 3, 3. Для этого ряда:
выборочная медианаd= 1, выборочное среднее 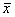 = 0
= 0
Дан вариационный ряд выборкиn= 8: –6, –2, 0, 3, 5, 7, 8, 9. Для этого ряда:
выборочная медианаd= 4, выборочное среднее 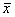 = 3
= 3
Дан вариационный ряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 11, 12, 15. Выборочная медиана для этого ряда – d равна
4,5
Дан вариационный ряд выборки объема n = 5: 1, 2, 5, 6, 7.Поставьте в соответствие:
Выборочная дисперсияS2== 5,36, Выборочное среднее 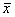 == 4,2, Медианаd== 5, размах == 6
== 4,2, Медианаd== 5, размах == 6
Дан вариационный ряд выборки объема n = 5: -2, 0, 1, 5, 6.Поставьте в соответствие:
Выборочная дисперсияS2== 9,2, Выборочное среднее 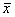 == 2, Медианаd== 1, размах == 8
== 2, Медианаd== 1, размах == 8
Дан вариационный ряд выборки объема n = 5: -2, 0, 1, 5, 6.Поставьте в соответствие:
Выборочная дисперсияS2== 9,2, Выборочное среднее 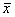 == 2, Медианаd== 1, размах == 8
== 2, Медианаd== 1, размах == 8
Дан вариационный ряд выборки объема n = 5: -2, -1, 0, 1, 3.Поставьте в соответствие:
Выборочная дисперсияS2== 2,96, Выборочное среднее 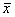 == 0,2, Медианаd== 0, размах == 5
== 0,2, Медианаd== 0, размах == 5
Дан вариационный ряд выборки объема n = 5: -2, -1, 0, 1, 3.Поставьте в соответствие:
Выборочная дисперсияS2== 2,96, Выборочное среднее 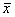 == 0,2, Медианаd== 0, размах == 5
== 0,2, Медианаd== 0, размах == 5
Дан вариационный ряд выборки объемаn= 7: –3, –1, 0, 2, 4, 6, 7. Медиана этого рядаd= _____ (наберите число).
Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12. Выборочная медиана для этого ряда – d равна
Дана выборка n = 5: -3, -1, 0, 1, 3. Выборочная дисперсия равна S2= _____ (наберите число)
Дана выборка n = 5: -3, -1, 0, 1, 3. Выборочная дисперсия равна S2= _____ (наберите число)
Дана выборка объемаn= 10: –1, –1, 2, 2, 2, 3, 3, 5, 5, 5. Статистическое распределение этой выборки имеет вид:

Дана выборка объема n = 5: 2, 3, 5, 7, 8. Выборочное среднее  = ______(наберите число)
= ______(наберите число)
Дана выборка объема n = 5: 2, 3, 5, 7, 8. Выборочное среднее  и выборочная дисперсия S2равны
и выборочная дисперсия S2равны
S2= 5,2,x = 5
Дана выборка объема n = 5: -2,-1,0, 3, 5. Выборочное среднее  и выборочная дисперсия S2равны
и выборочная дисперсия S2равны
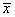 = 1,S2= 6,8
= 1,S2= 6,8
Дана выборка объема n = 5: -3, -2, 0, 2, 3. Выборочное среднее  и выборочная дисперсияS2равны
и выборочная дисперсияS2равны
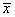 = 0,S2= 5,2
= 0,S2= 5,2
Дана выборка объемаn= 5: -4,-2,0,2,4. Выборочная дисперсияS2= ______(Наберите число)
Дана выборка объемаn= 5: -5,-3,0,3,5. Выборочная дисперсияS2= ______(Наберите число)
13.6
Дана выборка объемаn= 6: -4,-2,-1,0, 1, 2, 4. Выборочная дисперсияS2= ______(Наберите число)
Дана выборка объема n = 7: 3, 5, -2, 1, 0, 4, 3. Вариационный ряд для этой выборки и размах вариационного ряда
–2, 0, 1, 3, 3, 4, 5; размах равен 7
Дана выборка объемаn= 7: -5,-3,-1,0,1,3,5. Выборочная дисперсияS2= ______(Наберите число)
Дана выборка объема n: х1, х2, х3, …, хn. Ее выборочное среднее равно 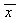 . Выборочная дисперсия находится по формуле (выберите две правильных)
. Выборочная дисперсия находится по формуле (выберите две правильных)
 ,
, 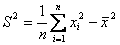
Данные о прибыли, полученной в течение месяца, за последние 5 месяцев оказались следующими:  С помощью метода наименьших квадратов по этим точкам строится прямая. Эта прямая для прибыли в мае даст значение (для получения этого значения строить прямую не надо) (наберите число)
С помощью метода наименьших квадратов по этим точкам строится прямая. Эта прямая для прибыли в мае даст значение (для получения этого значения строить прямую не надо) (наберите число)
Дано статистическое распределение выборки объема n=50 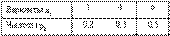 Эмпирическая функция распределения для этого ряда имеет вид
Эмпирическая функция распределения для этого ряда имеет вид

Дано статистическое распределение выборки с числом вариант m:  Верны ли утверждения?A) Выборочное среднее находится по формуле:
Верны ли утверждения?A) Выборочное среднее находится по формуле: 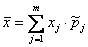 B) Выборочная дисперсия находится по формуле:
B) Выборочная дисперсия находится по формуле: 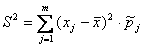
А - да, В - да
Два стрелка стреляют по разу в общую мишень. Вероятность попадания в цель у одного стрелка 0,8; у другого 0,6. Установите соответствие между вероятностями и их значениями. Установите соответствие между левыми и правыми частями таблицы
Цель не поражена == 0,08, Цель поражена двумя пулями == 0,48, Цель поражена хотя бы одной пулей == 0,92
