Главные оси и главные моменты инерции.

Начнем с определения:

Если для тензора второго ранга 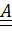существует вектор 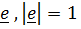такой, что 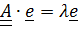, то число 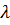называется главным (собственным) значением тензора, 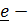собственным вектором, а ось, задаваемая 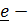главной осью тензора.

Теорема о приведении тензора инерции к главным осям.

Тензор инерции, как и любой симметричный тензор, имеет тройку ортогональных собственных векторов 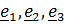и тройку вещественных собственных значений (главных моментов) 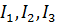, причем:

1. Если собственные значения различны, то собственные векторы определяются единственным образом и тензор инерции имеет вид

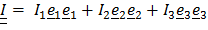
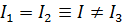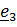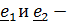2. Если два собственных значения равны, например , то однозначно определяется собственный вектор , а любые перпендикулярные к 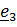(и друг к другу); в этом случае

.

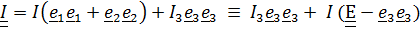Такой тензор называется трансверсально-изотропным; он не изменяется, если тело вращать вокруг оси изотропии, задаваемой .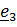

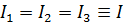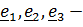3. Если равны все собственные значения , то любая

ортонормированная тройка и тензор инерции называется шаровым

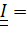
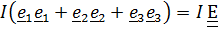
Эта теорема доказывается в курсе линейной алгебры как теорема о собственных числах (значениях) и собственных векторах симметричной матрицы.

Применительно к тензору инерции ее содержание сводится к тому, что существует, по меньшей мере, одна тройка главных осей, т.е. осей, относительно которых центробежные моменты инерции равны нулю и тензор инерции в этих осях имеет вид

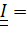
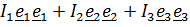
. Поскольку ориентация тройки осей задается тремя параметрами (например, углами Эйлера), то существует возможность сделать равными нулю трицентробежных момента.

В некоторых случаях, когда тело обладает каким – либо видом симметрии, то согласно физическому принципу Кюри-Неймана этой же симметрией должен обладать и тензор инерции; тогда главные оси могут быть найдены из соображений симметрии.

Так, например, если тело обладает плоскостью симметрии BXZ , то перпендикулярная ей ось Y является главной (рис.5.3а). Действительно, центробежные моменты 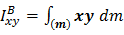и 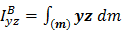равны нулю, поскольку каждому элементу 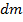с координатами 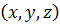соответствует симметричный с координатами .

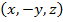Если имеется еще одна плоскость симметрии BYZ, перпендикулярная первой, то ось Х (а, следовательно, и Z) тоже главная: 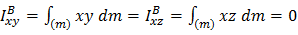,так что тензор инерции для любой точки В, находящейся на линии пересечения этих плоскостей, имеет вид .

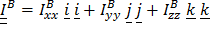B

X

Z

Y

a)

б

Z

В·

в)

Z

В·

Рис. 5.3. Симметричные тела

Если тело осесимметричное (рис.5.3б), то любая плоскость, содержащая ось Z , является плоскостью симметрии и, в дополнение ко всему вышесказанному ясно, что 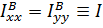; так что тензор инерции трансверсально-изотропный: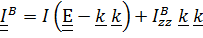

Если тело обладает осью симметрии «N» - го порядка, т.е. тело переходит «само в себя» при повороте на угол 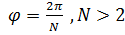(на рис.5.3в N=5), то можно доказать, что и в этом случае тензор инерции 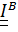трансверсально-изотропный.

Эллипсоид инерции.

Тензору инерции, как и всякому симметричному тензору, можно сопоставить наглядный геометрический объект – так называемую тензорную поверхность.

Пусть 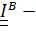тензор инерции в точке В. Построим квадратичную форму и приравняем ее единице:

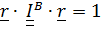(5.27)

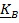X

Y

Z

B ·

· M

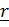Это уравнение поверхности, описываемой вектором с началом в точке В, которая для положительного тензора является эллипсоидом. Действительно, 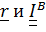в главных осях, получим: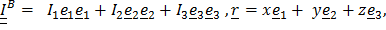

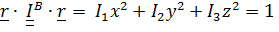или, в каноническом виде

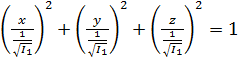(5.28)

Уравнение (5.38) – уравнение эллипсоида с полуосями, равными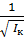

Так как протяженное в каком-либо направлении тело имеет относительно оси, совпадающей с этим направлением, наименьший момент инерции, то эллипсоид инерции приблизительно повторяет форму тела.

1. Найдем момент инерции 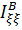относительно оси 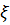, задаваемой вектором 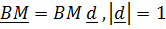. Имеем 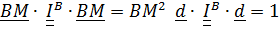, откуда

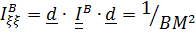
2. Вычислим дифференциал от уравнения (5.27):

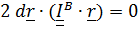, отсюда следует, что вектор 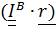перпендикулярен к эллипсоиду, поскольку вектор 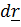лежит в касательной плоскости к поверхности.

Кинетический момент тела, вращающегося вокруг точки В, равен 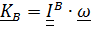, поэтому 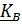направлен по нормали к поверхности эллипсоида в точке его пересечения с мгновенной осью вращения, проведенной через точку В.

3. Если тело обладает осью симметрии «N» - го порядка, т.е. переходит «само в себя» при повороте на угол 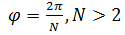( рис.5.3в ), то «вмороженный» в него эллипсоид инерции обладает тем же свойством и, следовательно, является эллипсоидом вращения с равными полуосями; т.е. тензор инерции 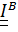трансверсально-изотропный.