Центр масс. Теорема о движении центра масс.
Центром масс (центром инерции) тела называется точка С, вектор положения которой задается формулой
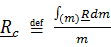( или, для системы точек, 
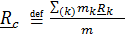), (5.6)
где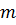 
- масса всего тела, 
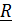- вектор положения элемента 
.
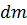Далее будем рассматривать закрытое тело.
Перепишем определение (5.6) в виде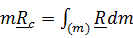 
и продифференцируем по времени:
.
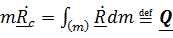Получили, что количество движения (импульс) тела равен произведению массы тела на скорость центра масс:
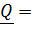
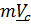(5.7)
Подставляя это выражение в закон (5.1), будем иметь
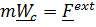,(5.8)
и, сравнивая с уравнением второго закона Ньютона, приходим к теореме о движении центра масс: центр масс тела движется как материальная точка с массой всего тела под действием силы, равной главному вектору внешних сил.
Если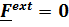 
,то скорость центра масс постоянна 
, 
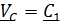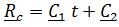
Другой пример. Из школьной физики известно, что при пренебрежении сопротивлением воздуха траектория снаряда, на которого действует сила тяжести – парабола. Из (5.8) следует, что при его взрыве в полете центр масс разлетевшихся осколков будет двигаться по той же траектории.
Центр масс обладает любопытным свойством: величина 
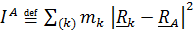(или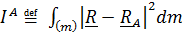 
)
- сумма произведений масс точек тела на квадраты расстояний до точки А, называемая полярным моментом инерции тела в точке A, минимальна, если в качестве точки А взять центр масс; иными словами, если в качестве меры расстояния принять произведение массы на квадрат расстояния до точки, то центр масс – точка, «ближайшая» ко всем точкам тела.
Заменим квадрат модуля скалярным произведением
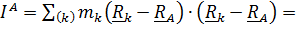
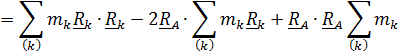
и, рассматривая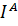 
как функцию 
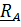, найдем дифференциал
.
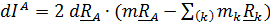Необходимое условие экстремума (в данном случае минимума) – равенство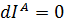 
, откуда вследствие произвольности 
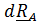получим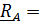 
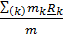
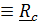
Уравнения динамики относительного движения материальной точки. Силы инерции.
Как уже отмечалось, уравнение 1-го ФЗМ для материальной точки имеет вид второго закона Ньютона (точку считаем закрытым телом)
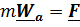. (5.9)
По теореме о сложении ускорений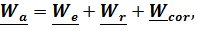 
,
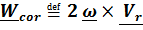поэтому (5.9) можем записать в виде
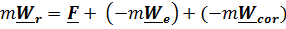, (5.10)
где величины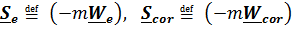 
по определениюназываются соответственно переносной и кориолисовой силами инерции.
Эти силы называют Эйлеровыми силами инерции, поскольку Эйлер получил их формулы в своих исследованиях законов движения жидкости во вращающихся каналах.
Силы инерции тождественно равны нулю в системах отсчета, движущихся поступательно и равномерно относительно исходной инерциальной. Эти системы образуют класс инерциальных систем отсчета.
Если наблюдатель в какой-либо системе отсчета обнаружит явления, противоречащие законам механики, в которых движения тел зависят от воздействий со стороны других физических тел, то либо не все воздействия учтены, либо его система отсчета неинерциальная.
Пример 1. Маятник Фуко.
Впервые публичная демонстрация была осуществлена французским физиком и астрономом
Жаком Фуко в 1851г. в Парижском Пантеоне: под куполом Пантеона он подвесил
металлический шар массой 28 кг с закреплённым на нём остриём на стальной проволоке
длиной 67м, крепление маятника позволяло ему свободно колебаться во всех направлениях,
под точкой крепления было сделано круговое ограждение диаметром 6 метров, по краю
ограждения была насыпана песчаная дорожка таким образом, чтобы маятник в своём
движении мог при её пересечении прочерчивать на песке отметки. Чтобы избежать бокового
толчка при пуске маятника, его отвели в сторону и привязали верёвкой, после чего верёвку
пережгли.
Маятник Фуко в Парижском Пантеоне
Период колебания маятника при такой длине подвеса составлял 16,4 секунд, при каждом колебании отклонение от предыдущего пересечения песчаной дорожки составляло ~3 мм, за час плоскость колебаний маятника повернулась более чем на 11° по часовой стрелке, то есть примерно за 32 часа совершила полный оборот и вернулась в прежнее положение.
| • |
 |
| |
 |
 |
 |
 |
 |
 |
 |
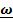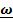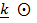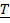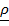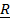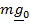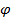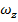| Z |
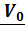. В инерциальной системе отсчета, в качестве которой можно взять систему, связанную с «неподвижными» звездами, уравнение движения имеет вид
,
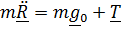где 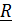- вектор положения маятника с началом в неподвижной точке системы отсчета ( например, в центре Земли), 
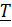- натяжение нити, а 
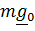- гравитационное притяжение Земли.
Ясно, что если начальная скорость лежит в плоскости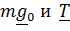 
, то маятник не выйдет из постоянной в инерциальной системе плоскости колебаний, что с точки зрения земного наблюдателя воспринимается как вращение этой плоскости по часовой стрелке с угловой скоростью 
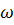. Если же маятник находится на широте 
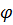, то плоскость колебаний вращается с угловой скоростью 
.
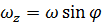Рассматривая движение маятника как сложное, состоящее из переносного вместе с Землей и относительного, запишем уравнение в виде (5.10)
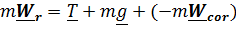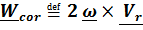, , где сумма 
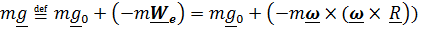–сила тяжести на данной широте. Решение этого уравнения даже в линейном приближении довольно громоздко, (смотри ниже), поэтому пока ограничимся тем, что «добавочная» сила инерции Кориолиса (- 
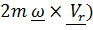направлена перпендикулярно скорости вправо, если смотреть вслед маятнику, чем и объясняется вращение плоскости колебаний по часовой стрелке. Заметим также, что линейное приближение дает ту же угловую скорость вращения .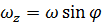