Мгновенный центр скоростей и способы его нахождения.

Из основной формулы кинематики твердого тела (4.3) ясно, что если 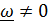, то можно найти такую точку P , скорость которой равна нулю – эта точка и называется мгновенным центром скоростей.

Для определения неизвестного вектора 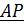из уравнения 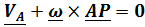умножим его слева векторно на 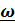и, раскрывая двойное векторное произведение, будем иметь

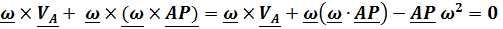, откуда

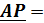
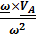(4.4)

Формула (4.4) предполагает, разумеется, известными 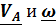, но во многих случаях мгновенный центр скоростей можно найти другими способами. Наиболее часто встречаются случаи:

1. Тело катится без проскальзывания.

Мгновенный центр скоростей находится в точке касания тела с неподвижной поверхностью.

Следующие случаи следуют из основной формулы, где в качестве полюса выбран мгновенный центр скоростей: 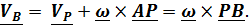( 4.5)

Отсюда следует, что: a) 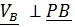- скорость всякой точки В перпендикулярна ,

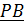b) 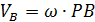- скорость всякой точки В пропорциональна расстоянию до точки P.

2. Если известна скорость одной точки A и линия, вдоль которой может быть направлена скорость другой точки B, то мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям. В этом случае вычисляется величина угловой скорости 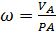, определяется ее направление и, соответственно, скорость точки В (см. рис 4.2).

Если перпендикуляры не пересекаются, то (мгновенно- поступательное движение) и скорости всех точек равны .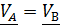

Если перпендикуляры слились, то мгновенный центр скоростей находится на пересечении линии, соединяющей концы векторов скорости и общего перпендикуляра.

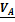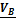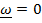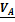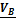· P

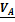· P

· P

Рис.4.2 . Мгновенный центр скоростей

Ускорения точек твердого тела при произвольном и плоском движении

Дифференцируя основную формулу кинематики твердого тела (4.3)

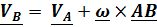, получаем формулу для ускорений

.

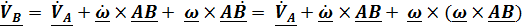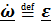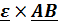
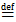
Производная вектора угловой скорости по времени называется вектором углового ускорения , слагаемое 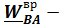вращательное ускорение точки В вокруг полюса А,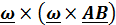 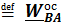- осестремительное ускорение. Таким образом

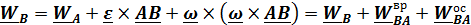, где

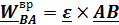,(4.6)

.

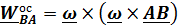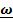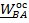A

BA

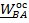A

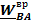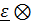B

Формулы (4.6) применимы для произвольного движения. Поясним термин «осестремительное ускорение». В теоретической механике линия, проходящая через полюс А параллельно вектору угловой скорости 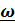,называется мгновенной осью вращения. Нетрудно убедиться, что двойное векторное произведение 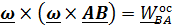направлено к мгновенной оси вращения под прямым углом, а его модуль равен 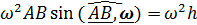, где h – расстояние от точки В до мгновенной оси вращения.

В случае плоского движения мгновенная ось вращения на плоском рисунке вырождается в точку- «центр», поэтому во многих учебниках 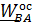называют «центростремительным» 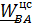. Векторы угловой скорости 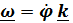и углового ускорения 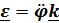перпендикулярны плоскости движения. Раскрывая двойное векторное произведение, получим

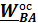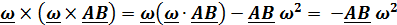= ,так как .

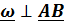Произвольное движение твердого тела