Скорость и ускорение в декартовой системе координат.
В декартовой системе вектор положения задается в виде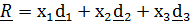 
, где 
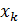- координаты вектора, а 
, 
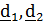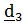– ортонормированный базис, т.е. базисные векторы единичные и взаимно-перпендикулярные. В этом случае координаты равны проекциям вектора на оси, задаваемые базисными векторами: 
.
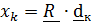Векторы скорости и ускорения равны
,
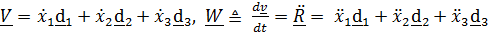а их модули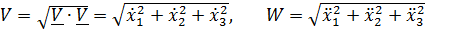 
Скорость и ускорение в цилиндрической системе координат
Вектор положения точки задается как функция цилиндрических координат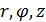 
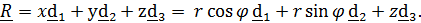(3.2)
В цилиндрической системекоординат, каки в любой другой системе, вводятся базисныевекторы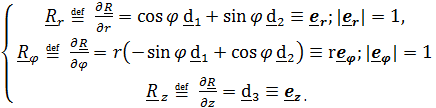 
(3.3)
Базисные векторы направлены по касательным к так называемым координатным линиям – линиям, получающимся при изменении только одной координаты.
Использование единичных базисных векторов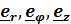 
удобно тем, что координаты вектора в единичном базисе имеют ту же размерность, что и сам вектор.
Дифференцируя (3.2), получим с учетом (3.3)
= 
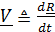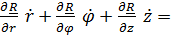
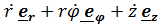(3.4)
Дифференцируя (3.4) и учитывая, что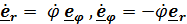 
,будем иметь
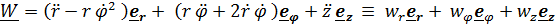(3.5)
Упражнение 2. Найти скорость и ускорение точки, движущейся по цилиндру.
| Y |
 |
 |
 |
 |
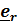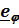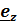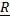| X |
| Z |
 |
 |
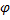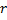| Z |
| • |
Уравнения движения
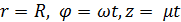(винтовая линия)Скорость и ускорение при траекторном (естественном) способе описания движения.
| n |
| τ |
 |
 |
 |
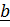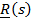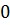| +S |
Уравнением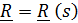 
задается линия, по которой движется точка; закон движения по ней 
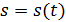, где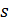 
– дуговая координата, т.е. длина дуги со знаком.
Базисные векторы вводятся следующим образом:
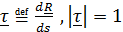– единичный вектор (орт ) касательной,
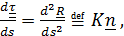где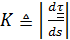 
- кривизна, а 
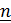- единичный вектор главной норма ли,
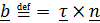–так называемый вектор бинормали.
Векторы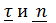 
лежат в так называемой соприкасающейся плоскости – предельном при 
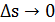положении плоскости, содержащей 
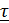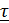(s) и (s+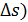 
. Кривизна 
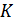характеризует скорость изменения направления касательной; обратную к ней величину 
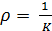. называют радиусом кривизны траектории.
Вектор скорости
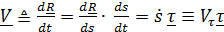, (3.6)
где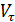 
является проекцией (единственной) вектора скорости на направление касательной и может быть любого знака.
Дифференцируя еще раз, получаем вектор ускорения
.
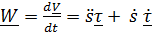Производную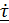 
также запишем как производную сложной функции
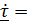
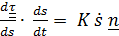, тогда
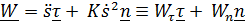, где (3.7)
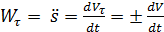- касательное (тангенциальное) ускорение,
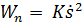
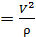- нормальное ускорение.
«Кинематический» подход часто используется дпя вычисления кривизны траектории при координатном способе задания движения. Вычисляется скорость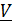 
и ее величина 
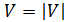, ускорение 
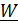и ее величина 
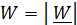, касательное ускорение 
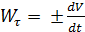, (либо 
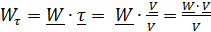), нормальное ускорение
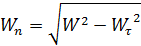и радиус кривизны 
.
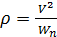Глава 4. Кинематика твердого тела
Твердым телом будем называть тело, расстояния между точками которого не изменяются в процессе движения.
Если в качестве модели реального объекта рассматривается тело, состоящее из тел-точек, положение которых описывается не только вектором положения, а и ориентацией (т.е. тела-точки могут вращаться), то в определение следует добавить слова « и взаимная ориентация не изменяется».