Равнодействующая, центр параллельных сил, центр тяжести.
Воздействия (силы и моменты) характеризуются главным вектором сил 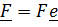 и главным моментом
и главным моментом 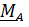 относительно произвольной опорной точки. Запишем формулу, связывающую моменты относительно двух точек – опорной точки
относительно произвольной опорной точки. Запишем формулу, связывающую моменты относительно двух точек – опорной точки  и так называемой точки приведения
и так называемой точки приведения 
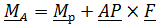 . (1)
. (1)
| A |
 |
 |
 |
| ⦁ P |
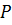 , относительно которой главный момент
, относительно которой главный момент 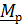 равен нулю, то говорят, что система приводится к равнодействующей, приложенной в точке приведения. Из формулы(1)
равен нулю, то говорят, что система приводится к равнодействующей, приложенной в точке приведения. Из формулы(1) 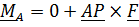 следует,что приведение к равнодействующей возможно, только если главный момент
следует,что приведение к равнодействующей возможно, только если главный момент 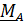 и главный век тор
и главный век тор 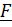 перпендикулярны. При этом множество точек приведения к равнодействующей находятся на прямой
перпендикулярны. При этом множество точек приведения к равнодействующей находятся на прямой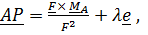 (2)
(2)
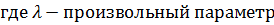 .
.
Рассмотрим систему параллельных сил 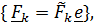 где
где 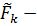 проекция
проекция 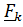 на направление, задаваемое вектором
на направление, задаваемое вектором 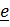 . Главный вектор
. Главный вектор 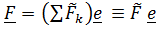 и главный момент
и главный момент 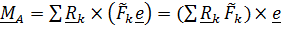 перпендикулярны, поэтому система приводится к равнодействующей. Покажем, что в этом случае на прямой (2) существует такая точка приведения
перпендикулярны, поэтому система приводится к равнодействующей. Покажем, что в этом случае на прямой (2) существует такая точка приведения  , называемая центром параллельных сил, положение которой не изменяется при повороте всех сил на произвольный угол (точки приложения сил не изменяются).
, называемая центром параллельных сил, положение которой не изменяется при повороте всех сил на произвольный угол (точки приложения сил не изменяются).
Подставляя выражения  и
и  в (2) и раскрывая двойное векторное произведение, получим
в (2) и раскрывая двойное векторное произведение, получим
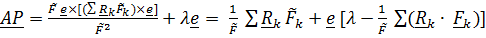 .
.
Чтобы это выражение не зависело от направления сил (вектора 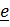 ), надо положить
), надо положить
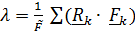 и тогда положение центра параллельных сил задается формулой
и тогда положение центра параллельных сил задается формулой 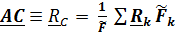 .(3)
.(3)
Частный случай параллельных сил – силы тяжести, действующие на точки тела. Если тело небольшого размера, то можно пренебречь различием в направлении сил (к центру Земли) и различиями в величине сил ввиду разного расстояния до центра Земли. Тогда центр тяжести совпадает с центром масс
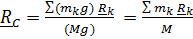 .
.
Оценим различие в положениях центра масс и центра тяжести «высокого» тела.
Пример. Центр тяжести небоскреба.
| dz |
| R |
| z |
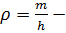 линейная плотность массы. Сила тяжести, действующая на элемент массы
линейная плотность массы. Сила тяжести, действующая на элемент массы 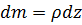 равна
равна 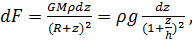 где
где 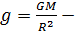 ускорение на поверхности Земли. Суммарная сила тяжести
ускорение на поверхности Земли. Суммарная сила тяжести 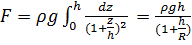 . Координата центра тяжести
. Координата центра тяжести
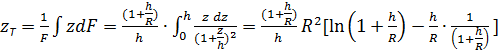 .
.
Заменяя 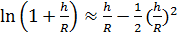 , получим
, получим 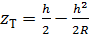 . Для высоты
. Для высоты 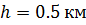 получим, что центр тяжести ниже центра масс всего лишь на
получим, что центр тяжести ниже центра масс всего лишь на 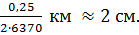
Глава 3. Кинематика точки
| A |
 |
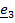 |
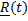 |
| • |
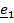 |
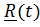 как функцией времени, проведенным в точку из некоторого неподвижного в системе отсчета центра A:
как функцией времени, проведенным в точку из некоторого неподвижного в системе отсчета центра A: Траекторией называется кривая, по которой движется точка, скоростью 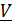 – производная по времени вектора положения R , ускорением
– производная по времени вектора положения R , ускорением 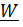 - производная от вектора скорости
- производная от вектора скорости
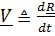
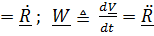 . (3.1)
. (3.1)
Из определения производной вектора следует, что вектор скорости направлен по касательной к траектории. Собственно говоря, формулами (3.1) вся кинематика точки и исчерпывается; все технические трудности связаны лишь с выбором системы координат.
Упражнение 1. Исходя из определения производной вектор-функции от скалярного аргумента 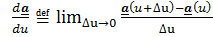 показать, что
показать, что
1) 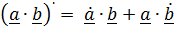 (производная скалярного произведения)
(производная скалярного произведения)
2) 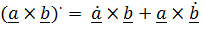 (производная векторного произведения
(производная векторного произведения
3) Если 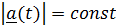 , то
, то 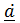 ^
^ 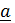 (продифференцировать квадрат модуля, равный
(продифференцировать квадрат модуля, равный 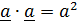 ).
).
