Некоторые сведения из векторного анализа.
Оглавление
Оглавление. 2
Глава 1. Введение. 6
1.1. Системы отсчета, системы координат. Тела, примеры тел в механике. 6
1.2. Некоторые сведения из векторного анализа. 7
1.3. Некоторые сведения из тензорного анализа. 11
1.3.1. Определение тензора второго ранга. 11
1.3.2. Операции с тензорами второго ранга. 12
1. Транспонирование и разложение тензора на симметричную и кососимметричную части. 12
2.Тензорный базис, координаты тензора. Матричный образ тензора. 12
3. Скалярное и векторное умножение тензора на вектор и тензор. Единичный тензор. 13
4.След, векторный инвариант, определитель тензора. Теорема о представлении кососимметричного тензора. 14
1.3.3. Некоторые тождества, связанные с определителем тензора. 15
1.3.4. Ортогональные тензоры. Тензор поворота. 16
Глава 2. Статика. 17
2.1. Воздействия и их классификация. Главный вектор и главный момент воздействий. Зависимость главного момента от выбора опорной точки. 17
2.2. Уравнения равновесия для произвольной и плоской систем воздействий. Момент относительно оси. Типы опорных реакций. Статически определимые и неопределимые системы. 19
2.3. Эквивалентные воздействия. 21
2.4. Равнодействующая, центр параллельных сил, центр тяжести. 23
Глава 3. Кинематика точки. 24
3.1 Скорость и ускорение в декартовой системе координат. 24
3.2 Скорость и ускорение в цилиндрической системе координат. 25
3.3. Скорость и ускорение при траекторном (естественном) способе описания движения. 26
Глава 4. Кинематика твердого тела. 27
4.1 Кинематика плоского движения. 27
4.1.1 Основная формула кинематики твердого тела. Формула Эйлера. 27
4.1.2 Мгновенный центр скоростей и способы его нахождения. 28
4.1.3. Ускорения точек твердого тела при произвольном и плоском движении. 29
4.2.Произвольное движение твердого тела. 30
4.2.1 Описание ориентации тела. Направляющие косинусы. 30
4.2.2. Углы Эйлера, самолетные (корабельные) углы. 31
4.2.3.Матрица поворота. Матрица спина. Вектор угловой скорости. 33
4.2.4. Описание ориентации с помощью тензора поворота. Теорема Эйлера о тензоре поворота. 35
4.2.5 . Тензор спина, вектор угловой скорости, формула Пуассона. 37
4.2.6.Теорема о сложении угловых скоростей. 37
4.2.7. Примеры вычисления вектора угловой скорости. 39
Пример 1. Углы Эйлера. 39
Пример 2. Самолетные (корабельные) углы. 40
Пример 3. Трехстепенной гироскоп в кардановом подвесе. 41
Пример 4. Движение конуса по конусу. 42
4.2.8. Связь тензора поворота и вектора конечного поворота . 43
4.2.9.Сложное движение точки. Теоремы о сложении скоростей и ускорений (теорема Кориолиса). 44
4.2.10. Сложное движение тела. 46
Глава 5. Фундаментальные законы механики. 49
5.1. Первый фундаментальный закон механики - закон баланса количества движения. Открытые и закрытые тела. 49
Пример. Уравнение Мещерского. Формула Циолковского. 50
5.1.1. Центр масс. Теорема о движении центра масс. 51
5.1.2. Уравнения динамики относительного движения материальной точки. Силы инерции. 52
Пример 1. Маятник Фуко. 52
Пример 2. Отклонение снарядов (битва у Фолклендских островов). 55
5.2. Второй фундаментальный закон механики - закон баланса момента количества движения (кинетического момента, момента импульса). 57
5.2.1. Зависимость кинетического момента от выбора опорной точки. Кинетический момент твердого тела. Тензор инерции. 58
5.2.2. Постоянный тензор инерции. Осевые и центробежные моменты инерции. Вычисление моментов инерции относительно произвольных осей. 59
5.2.3. Зависимость тензора инерции от точки (обобщенная теорема Гюйгенса- Штейнера). 61
5.2.4. Главные оси и главные моменты инерции. 62
5.2.5. Эллипсоид инерции. 63
5.2.6. Вычисление тензоров инерции некоторых тел (шар, цилиндр, конус). 64
5.2.7.Дифференциальное уравнение вращения вокруг неподвижной оси. Физический маятник. 66
5.2.8. Дифференциальные уравнения произвольного движения твердого тела. Замена опорной точки во втором фундаментальном законе. 67
Пример 1. Качение шара по вращающейся плоскости. 69
Пример 2. Качение шара по внутренней поверхности вертикального цилиндра. 70
5.2.9. Динамические реакции оси вращающегося тела. Пример. 71
5.3. Третий фундаментальный закон механики (закон баланса энергии). 73
5.3.1. Кинетическая энергия материальной точки и твердого тела. Теорема Кенига. 73
5.3.2. Мощность, работа. Потенциальные воздействия. 74
5.3.3. Примеры потенциальных воздействий. 75
5.3.4. Теорема об изменении кинетической энергии. 76
5.3.5. Третий фундаментальный закон механики (закон баланса энергии). 76
Глава 6. Механика Лагранжа. 78
6.1.Обобщенные координаты, связи, число степеней свободы. 78
6.2. Уравнения Лагранжа (второго рода). 79
Замечание 1. Вычисление обобщенных сил для потенциальных воздействий. 81
Замечание 2. Принцип возможных скоростей. 81
Замечание 3. Обобщенные силы, обеспечивающие постулируемую зависимость координат от времени. Примеры. 82
Пример 1. Математический маятник с изменяющейся длиной. 82
Пример 2. Движение тележки по вращающемуся стержню. 82
Замечание 4. О неголономных системах. Пример. 83
Глава 7. Колебания систем.. 87
7.1. Колебания системы с одной степенью свободы. 87
7.1.1. Свободные колебания без сопротивления. 88
7.1.2. Вынужденные колебания без сопротивления при гармоническом воздействии. Резонанс. 88
7.1.3. Вынужденные колебания без сопротивления при произвольном воздействии. Интеграл Дюамеля. 89
7.1.4. Свободные колебания с учетом сопротивления. 90
7.1.5. Вынужденные колебания с учетом вязкого сопротивления. 92
Пример. Малые колебания кривошипно-шатунного механизма. 93
7.2. Колебания системы с несколькими степенями свободы. 95
7.2.1. Линеаризация уравнений движения вблизи положения равновесия. 95
7.2.2 Устойчивость положения равновесия. 97
7.2.3. Собственные частоты и формы малых колебаний. 97
7.2.4. Общее решение задачи о свободных колебаниях. 99
7.2.5. Главные (нормальные) координаты.. 100
7.2.6. Вынужденные колебания системы с несколькими степенями свободы. 103
1.Разложение по формам свободных колебаний (метод главных координат). 103
2. Случай гармонических обобщенных сил. Пример: динамический гаситель. 104
7.3. Колебания упругих тел с распределенными параметрами. 105
7.3.1. Метод Рэлея-Ритца. 106
Пример 1. Свободные изгибные колебания консольного клина переменного круглого сечения. 107
7.3.2. Метод конечных элементов (МКЭ). 108
Пример 2. Продольные колебания консольного стержня постоянного сечения. 109
Литература. 110
Глава 1. Введение.
1.1. Системы отсчета, системы координат. Тела, примеры тел в механике.
Все явления в окружающем нас мире могут быть описаны только в системах отсчета, посредством которых можно указать место и время события.
Введем тройку не лежащих в одной плоскости (некомпланарных) направленных из точки А отрезков (векторов)  называемых отсчетнымр
называемых отсчетнымр  пером и заполним пространство точками, положение которых задается векторами
пером и заполним пространство точками, положение которых задается векторами
 ,
,  (1.1)
(1.1)
где вещественные числа  называются отсчетными координатами.
называются отсчетными координатами.
 |
 |
 |
 |
 |
| Рис.1.1.Система отсчета |
Отсчетный репер (А,
 с множеством точек (1.1) называется телом отсчета.
с множеством точек (1.1) называется телом отсчета. Система отсчета – это тело отсчета с прибором для измерения времени (часами) (рис.1.1). Только в системе отсчета могут быть введены основные понятия, в том числе расстояние и направление. В системе отсчета можно ввести сколько угодно систем координат, в том числе и подвижных, но, скажем, ни скорость точки, ни ускорение от системы координат не зависят.
Механика не изучает реальные физические объекты ввиду их неодолимой сложности; она изучает тела - математические модели, наделенные некоторыми общими свойствами реальных объектов.
Основными «кирпичиками», из которых составляются тела, являются материальная точка и твердое тело, которые, собственно, и являются основными объектами изучения в общем курсе теоретической механики.
Материальная точка – наделенная массой тело, для описания положения которого достаточно одного лишь вектора положения. Так, если нас интересует только положение Земли на ее орбите, мы считаем Землю материальной точкой и описываем положение, скажем, ее центра; в то же время при описании движения какой-либо элементарной частицы необходимо учитывать и ее вращение – а это уже, по меньшей мере, модель твердого тела. Как станет ясно из дальнейшего, для твердого тела кроме вектора положения какой-либо его точки необходимо еще тремя координатами (углами) описать его ориентацию.
Кроме того, взаимодействие материальных точек описывается только силами, а твердых тел еще и моментами.
Тела можно разделить на одномерные, двумерные и трехмерные.
Одномерные тела занимают линию в пространстве и могут состоять из материальных точек (нити) и твердых тел-точек (стержни). Двумерные тела занимают поверхность в пространстве и также могут состоять из материальных точек (мембраны) и тел-точек (оболочки).
Трехмерные модели занимают объем .
Глава 2. Статика
Статика изучает условия равновесия (покоя) тел в какой-либо системе отсчета. Поскольку в покое скорости равны нулю, тело можем называть твердым, но это не обязательно.
Эквивалентные воздействия
Эквивалентными воздействиями в теоретической механике называют воздействия, которые при замене одной системы воздействий на другую не изменяют движения (в частности, состояния покоя) тела.
Если рассматривается твердое тело, то есть тело, находящееся в покое или совершающее жесткое движение, то, как следует из законов механики, необходимыми условиями эквивалентности являются равенства главных векторов и главных моментов воздействий.
Рассмотрим наиболее часто встречающиеся в учебных задачах статики случаи равномерно и линейно-распределенной нагрузки.
| A |
| y |
| Zz |
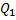 |
| X |
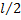 |
| Xy |
| y |
| A |
| Z |
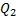 |
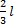 |
В случае равномерно - распределенной нагрузки ее линейная плотность (сила на единицу длины) 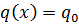 , для линейно-распределенной
, для линейно-распределенной 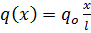 . Найдем главные векторы и проекции на ось Z главных моментов относительно, например, точки А.Имеем
. Найдем главные векторы и проекции на ось Z главных моментов относительно, например, точки А.Имеем
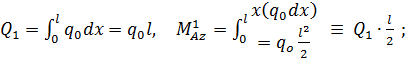
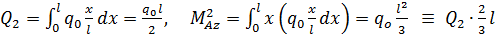 .
.
Полученные формулы показывают, что для быстрого составления уравнений равновесия удобно заменить распределенные нагрузки сосредоточенными силами 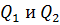 . Собственно говоря, применение эквивалентности на этом и заканчивается.
. Собственно говоря, применение эквивалентности на этом и заканчивается.
Замечание 1.
В учебных задачах на равновесие систем тел необходимым элементом является определение реакций в соединениях этих тел, например, в шарнирах.
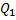 |
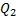 |
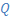 |
Для получения правильного результата следует заменить распределенную нагрузку на участках по разные стороны от шарнира сосредоточенными силами 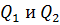 , но не на одну силу
, но не на одну силу 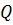 (см. рис.).
(см. рис.).
Замечание 2.
Попытки придать понятию «эквивалентность» некий универсальный смысл, распространив его и на произвольную систему материальных точек [2] и тем самым на деформируемое тело вообще лишены смысла, поскольку в этом случае понятие эквивалентности сводится лишь к замене одной силы в точке на сумму сил в этой же самой точке.
Глава 3. Кинематика точки
| A |
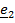 |
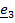 |
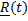 |
| • |
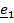 |
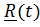 как функцией времени, проведенным в точку из некоторого неподвижного в системе отсчета центра A:
как функцией времени, проведенным в точку из некоторого неподвижного в системе отсчета центра A: Траекторией называется кривая, по которой движется точка, скоростью 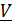 – производная по времени вектора положения R , ускорением
– производная по времени вектора положения R , ускорением 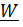 - производная от вектора скорости
- производная от вектора скорости
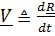
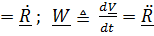 . (3.1)
. (3.1)
Из определения производной вектора следует, что вектор скорости направлен по касательной к траектории. Собственно говоря, формулами (3.1) вся кинематика точки и исчерпывается; все технические трудности связаны лишь с выбором системы координат.
Упражнение 1. Исходя из определения производной вектор-функции от скалярного аргумента 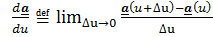 показать, что
показать, что
1) 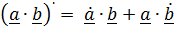 (производная скалярного произведения)
(производная скалярного произведения)
2) 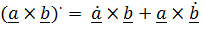 (производная векторного произведения
(производная векторного произведения
3) Если 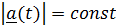 , то
, то 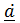 ^
^ 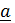 (продифференцировать квадрат модуля, равный
(продифференцировать квадрат модуля, равный 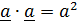 ).
).
Примеры вычисления вектора угловой скорости.
Пример 1. Углы Эйлера
| Рис. 4.9. Углы Эйлера. |
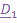 |
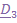 |
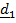 |
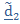 |
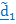 |
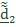 |
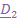 |
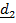 |
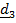 |
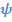 |
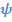 |
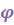 |
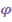 |
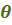 |
| Рис. 4.10. Углы Эйлера (волчок) |
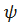 |
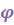 |
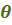 |
Традиционно углы Эйлера вводятся следующим образом. Переход из отсчетного положения
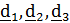 в актуальное
в актуальное 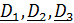 осуществляется тремя поворотами (рис.4.9):
осуществляется тремя поворотами (рис.4.9): 1. Поворот вокруг 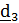 на угол прецессии
на угол прецессии 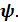 При этом
При этом 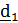 переходит в положение
переходит в положение
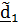 ,(
,( 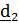 в
в 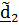 ). Этот поворот описывается тензором
). Этот поворот описывается тензором 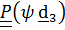
2. Поворот вокруг 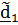 на угол нутации
на угол нутации 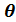 . При этом
. При этом 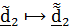 ,
, 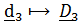 .
.
Этот поворот описывается тензором 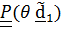
3. Поворот вокруг 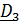 на угол собственного вращения
на угол собственного вращения 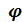 – тензор
– тензор 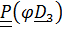 .
.
Таким образом, результирующий тензор поворота равен
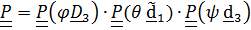 (4.26)
(4.26)
Для наглядности на рис.4.10 изображен волчок и углы Эйлера, описывающие его ориентацию.
Покажем, что традиционная последовательность поворотов (4.26) может быть заменена на последовательность поворотов на те же самые углы вокруг неподвижных осей:
1. Поворот вокруг 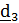 на угол собственного (чистого) вращения
на угол собственного (чистого) вращения 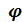
2. Поворот вокруг 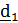 на угол нутации
на угол нутации 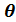 .
.
3. Поворот вокруг 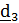 на угол прецессии
на угол прецессии 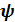
Поскольку 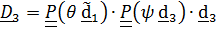 ,
, 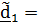
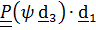 то по теореме (4.19)
то по теореме (4.19)
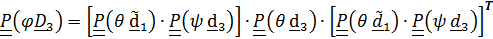 ,
,
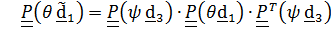 .
.
Подставляя эти выражения в (4.26), получим с учетом 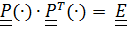
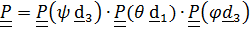 .
. 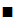 (4.27)
(4.27)
Разумеется, преимущество (4.27) по сравнению с (4.26) в том, что оси поворотов неподвижны.
Вектор угловой скорости по теореме о сложении угловых скоростей (4.23) равен
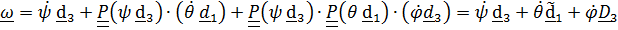 .
.
Это же (правильное) выражение обычно получают из (4.26), применяя правдоподобные рассуждения о сложении « бесконечно малых» поворотов; применив их к другой последовательности поворотов, например (4.27), получим абсолютно неверный результат 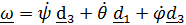 .
.
Из (4.27) видно, что при малом угле нутации 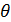 , когда
, когда 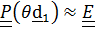 тензор поворота
тензор поворота
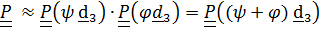 - углы
- углы 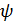 и
и 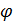 в линейном приближении становятся неразличимыми и входят в уравнения в виде суммы (
в линейном приближении становятся неразличимыми и входят в уравнения в виде суммы ( 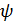 +
+ 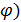 . В этом неудобство углов Эйлера.
. В этом неудобство углов Эйлера.
Пример 2. Самолетные (корабельные) углы.
Этого недостатка лишены самолетные (корабельные) углы (рис.4.11).
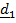 |
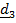 |
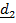 |
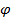 |
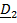 |
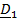 |
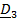 |
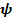 |
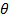 |
| Рис.4.11. Самолетные углы |
Переход из отсчетного положения 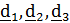 в актуальное
в актуальное 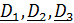 можно осуществить тремя поворотами (повернуть самостоятельно!) (рис.4.11):
можно осуществить тремя поворотами (повернуть самостоятельно!) (рис.4.11):
1. Поворот вокруг 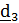 на угол рысканья
на угол рысканья 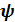 , при этом
, при этом 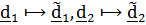
2. Поворот вокруг 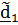 на угол тангажа
на угол тангажа 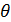 , при этом
, при этом 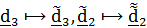
4.Поворот на угол крена 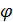 вокруг
вокруг 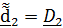 .
.
Тензор поворота равен 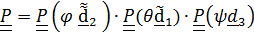 (4.28)
(4.28)
Выражение «можно осуществить» неслучайное; нетрудно понять, что возможны и другие варианты, например, повороты вокруг фиксированных осей. Применяя теорему о тензоре поворота с повернутой осью (4.19) из того, что 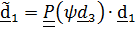 ,
, 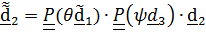 , будем иметь
, будем иметь
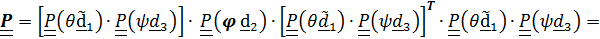
= 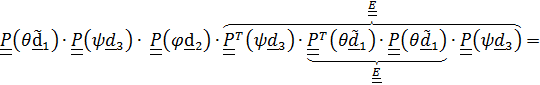
= 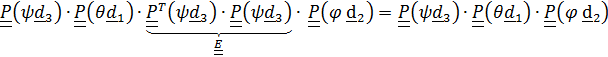 .
.
Таким образом, получили следующую композицию поворотов:
1. Поворот вокруг 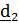 на угол крена
на угол крена 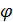 (рискуя сломать крылья)
(рискуя сломать крылья)
2. Поворот вокруг 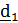 на угол тангажа
на угол тангажа 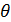 (подъем «носа»)
(подъем «носа»)
4. Поворот вокруг 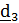 на угол рысканья
на угол рысканья 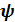
Тензор поворота и вектор угловой скорости имеют вид
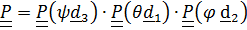 (4.29)
(4.29)
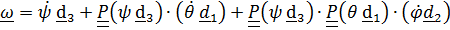
Пример 3. Трехстепенной гироскоп в кардановом подвесе.
| ротор |
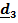 |
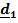 |
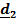 |
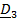 |
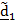 |
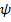 |
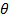 |
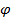 |
| Рис.4.12. Трехстепенной гироскоп |
Карданов подвес имеет три физических оси поворота, поэтому нетрудно догадаться, как тремя поворотами вокруг неподвижных осей перевести ротор гироскопа из отсчетного положения в актуальное .Разумеется, последовательность поворотов может быть любой, но, как мы убедились, повороты вокруг неподвижных осей самые удобные.
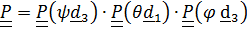 ,
,
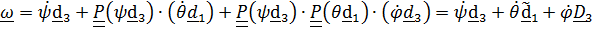 . (4.30)
. (4.30)
Физические оси позволяют правильно найти угловую скорость как сумму угловых скоростей вращений вокруг этих осей в актуальном положении.
Пример 4. Движение конуса по конусу
| D |
| Рис.4.13. Качение конуса(шестерни) |
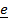 |
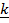 ψ ψ |
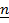 |
| α |
| βα |
| φ |
| b |
| K |
| A |
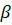 |
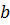 |
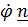 |
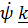 |
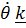 |
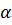 |
| Z |
| X |
| Y |
Ориентация подвижного конуса (шестерни) задается двумя углами – углом поворота
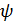 вокруг неподвижной оси (вектора
вокруг неподвижной оси (вектора 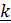 ) и углом
) и углом 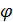 вращения вокруг собственной оси, актуальное положение которой задается вектором
вращения вокруг собственной оси, актуальное положение которой задается вектором 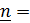
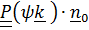 .
. Тензор поворота 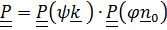 - повороты вокруг неподвижных осей.
- повороты вокруг неподвижных осей.
Вектор угловой скорости 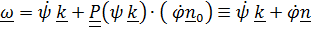 . (4.31)
. (4.31)
Если нет проскальзывания, то длина дуги окружности основания неподвижного конуса равна длине соответствующей дуги подвижного: 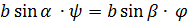 , откуда
, откуда 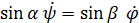 и
и 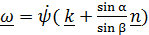 . Векторное произведение угловой скорости на вектор
. Векторное произведение угловой скорости на вектор 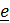 касающихся образующих конусов равно нулю:
касающихся образующих конусов равно нулю: 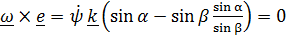 , следовательно,
, следовательно, 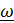 параллелен
параллелен 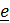 (см.рис.4.13).
(см.рис.4.13).
Впрочем, геометрическому подходу следует предпочесть кинематический. Так, если вращается и нижняя шестерня (конус), то для нахождения угловой скорости проще исходить из равенства скоростей в точке контакта К:
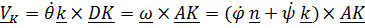 .
.
Проецируя эту формулу на ось 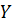 , получим
, получим 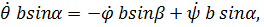
откуда 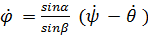 .
.
Дифференцируя угловую скорость (4.31), получим угловое ускорение
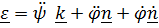 и с учетом
и с учетом 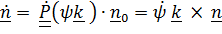
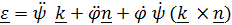
Сложное движение тела
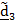 |
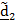 |
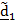 |
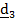 |
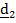 |
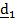 |
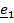 |
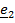 |
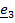 |
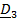 |
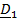 |
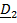 |
| Рис.4.16 |
Рассматривается движение тела («летающей тарелки») относительно двух систем отсчета - неподвижной с ортами
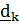 и подвижной с ортами
и подвижной с ортами 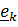 (рис 4.16).
(рис 4.16). Необходимо определить абсолютную ориентацию тела по известной ориентации подвижной системы и относительной ориентации, информация о которой может быть передана в неподвижную систему любым способом, например, в виде телевизионной картинки или в числовом виде посредством направляющих косинусов 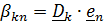 , измеряемых подвижным наблюдателем.
, измеряемых подвижным наблюдателем.
Тензор поворота, описывающий «абсолютную» ориентацию 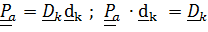 ; описывающий переносное движение
; описывающий переносное движение 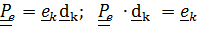 . Тензор поворота относительной ориентации введем в виде
. Тензор поворота относительной ориентации введем в виде 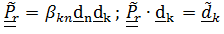 , т.е. этот тензор действительно описывает то движение, которое «видит» подвижный наблюдатель, одушевленный или неодушевленный (например, телекамера) и которое неподвижный может наблюдать на экране телевизора. Таким образом,
, т.е. этот тензор действительно описывает то движение, которое «видит» подвижный наблюдатель, одушевленный или неодушевленный (например, телекамера) и которое неподвижный может наблюдать на экране телевизора. Таким образом,
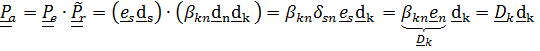 (4.41)
(4.41)
Вектор угловой скорости по теореме о сложении угловых скоростей имеет вид
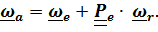 (4.42)
(4.42)
Вектор углового ускорения
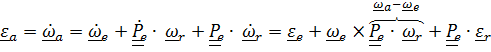 , или
, или
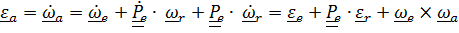 (4.43)
(4.43)
Существует и другая [4] интерпретация сложного движения, которая в части описания ориентации по сути не отличается от вышеизложенного подхода, а вот в части определения относительной угловой скорости отличается существенно .
Тензор поворота переносного движения, как и ранее 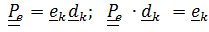 .
.
Тензором относительного поворота называется 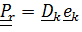 ;
; 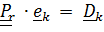 .Действительно, матрица компонент этого тензора, записанного в базисе
.Действительно, матрица компонент этого тензора, записанного в базисе 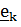 , описывает относительную ориентацию
, описывает относительную ориентацию 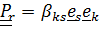 .
.
Очевидно, что тензор поворота абсолютного движения
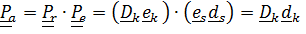 .
.
Сразу же отметим, что 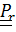 - это повернутый вместе с подвижной системой «истинный» тензор поворота относительного движения
- это повернутый вместе с подвижной системой «истинный» тензор поворота относительного движения 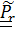 :
:
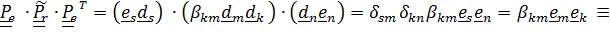
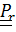 ,
,
так что 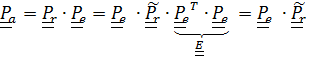 – формула (4.41).
– формула (4.41).
Векторы абсолютной и переносной угловых скоростей вводятся обычным способом в соответствии с формулой Пуассона 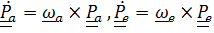 , а вот вектор относительной угловой скорости
, а вот вектор относительной угловой скорости 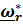 определяется таким образом, чтобы формула сложения угловых скоростей имела привычный (см. любой учебник) вид
определяется таким образом, чтобы формула сложения угловых скоростей имела привычный (см. любой учебник) вид
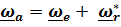 . (4.44)
. (4.44)
Для этого 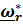 вводится формулой
вводится формулой
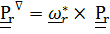 , (4.45)
, (4.45)
где 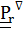 - производная Яуманна, известная в теоретической механике как относительная производная. Так, если вектор задан координатами в подвижном базисе
- производная Яуманна, известная в теоретической механике как относительная производная. Так, если вектор задан координатами в подвижном базисе 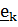 , то полная производная по времени имеет вид
, то полная производная по времени имеет вид
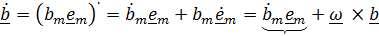 ,
,
где подчеркнутое слагаемое – относительная производная, т.е. производная, которую вычислял бы подвижный наблюдатель, для которого базисные векторы 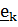 неподвижны. Таким образом,
неподвижны. Таким образом, 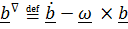 .
.
Совершенно аналогично для тензора
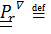
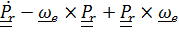 . (4.46)
. (4.46)
Дифференцируя 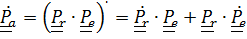 и заменяя
и заменяя 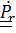 по (4.46), (4.45), придем к (4.44).
по (4.46), (4.45), придем к (4.44).
Собственно говоря, из (4.42) следует, что 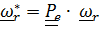 , то есть это повернутый вместе с подвижной системой (вместе с телевизором ) «истинный» вектор угловой скорости относительного движения
, то есть это повернутый вместе с подвижной системой (вместе с телевизором ) «истинный» вектор угловой скорости относительного движения 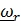 . При графоаналитическом решении задач, когда, разумеется, рассматривается актуальное состояние, именно
. При графоаналитическом решении задач, когда, разумеется, рассматривается актуальное состояние, именно 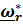 изображается на рисунках.
изображается на рисунках.
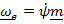 |
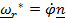 |
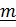 платформу, относительно которой вокруг оси с ортом
платформу, относительно которой вокруг оси с ортом 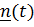 вращается тело (см.рис.).
вращается тело (см.рис.). Введем подвижную систему отсчета, связанную с платформой.
. Тензор поворота переносного движения 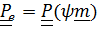 . Тензор поворота относительного движения («истинный»)
. Тензор поворота относительного движения («истинный») 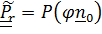 , где
, где 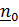 - орт оси поворота тела в отсчетном положении. Заметим, что для подвижного наблюдателя постоянный вектор
- орт оси поворота тела в отсчетном положении. Заметим, что для подвижного наблюдателя постоянный вектор 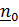 остается неподвижным и впредь. Разумеется, по (4.41),(4.42)
остается неподвижным и впредь. Разумеется, по (4.41),(4.42)
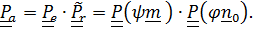 (4.47)
(4.47)
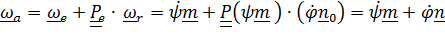 .
.
При втором подходе 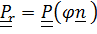 ,
, 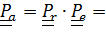
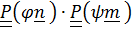 ,
, 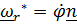 (вектор
(вектор 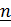 считается постоянным). Так как
считается постоянным). Так как 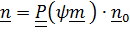 , то по теореме (4.19)
, то по теореме (4.19) 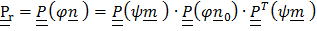 и, как отмечалось выше, получим (4.47).
и, как отмечалось выше, получим (4.47).
Пример. Уравнение Мещерского. Формула Циолковского.
| x |
 |
 |
 где
где  «сухая» масса ракеты,
«сухая» масса ракеты,  масса топлива в ракете. Заметим, что описать движение закрытого тела постоянной массы
масса топлива в ракете. Заметим, что описать движение закрытого тела постоянной массы  – ракеты с уже сгоревшим топливом (газом) практически невозможно, поскольку это потребовало бы задания сил, действующих не только на ракету, но и на сгоревшее топливо .
– ракеты с уже сгоревшим топливом (газом) практически невозможно, поскольку это потребовало бы задания сил, действующих не только на ракету, но и на сгоревшее топливо . Запишем уравнение первого фундаментального закона
 .
.
Количество движения  . В главный вектор внешних сил
. В главный вектор внешних сил  входят сила тяжести, аэродинамические силы и, строго говоря, давление на срезе сопла двигателя.
входят сила тяжести, аэродинамические силы и, строго говоря, давление на срезе сопла двигателя.
Скорость подвода количества движения 
где  масса отделяющегося за время
масса отделяющегося за время  газа ,
газа ,  его скорость, а знак (-1) учитывает факт именно отделения.
его скорость, а знак (-1) учитывает факт именно отделения.
Поскольку  то
то  Таким образом,
Таким образом,
