Финальные вероятности состояний

Финальные вероятности состояний характеризуют систему в предельном стационарном режиме. Когда процесс длится достаточно долго, возникает вопрос о предельном поведении вероятностей P_i(t) при t®¥.

Если все потоки событий, переводящие систему из одного состояния в другое, являются простейшими, т.е. стационарными (пуассоновскими) с постоянными интенсивностями l_ij, то в некоторых случаях существуют финальные (или предельные) вероятности состояний,

P=lim P_i(t) (i=1,2,...,n),

t®¥

не зависящие от того, в каком состоянии система S находилась в начальный момент времени. Это значит, что в системе S с течением времени устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятность состояний уже не меняется. В этом предельном режиме каждая финальная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии.

Коэффициент готовности

Коэффициент готовности - асимптотическое значение функции готовности К(t) при неограниченном возрастании аргумента t (см. рис. 37):

K=lim K(t).

t®¥

Он определяется по формулам (71) или (72) и с учетом формулы (65). Так как T_ср= 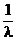, то

K= .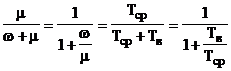

Коэффициент готовности является финальной вероятностью работоспособного состояния восстанавливаемого объекта с конечным временем восстановления и может быть истолкован как среднее относительное время пребывания объекта в этом состоянии в предельном стационарном режиме эксплуатации.

Повышение коэффициента готовности достигается либо увеличением среднего времени безотказной работы, либо уменьшением среднего времени восстановления, либо одновременным увеличением среднего времени безотказной работы и уменьшением среднего времени восстановления. Хотя коэффициент готовности определен как асимптотическая величина при t®¥, его можно использовать при любых конечных значениях времени t, для которых

|K(t)-K|<e,

где e - заданная погрешность (например, e=0,01).

Коэффициент простоя

Коэффициент простоя - асимптотическое значение функции простоя k(t) при неограниченном возрастании аргумента t (см. рис. 38)

k=lim k(t).

t®¥

Он определяется по формулам (73) или (74) при t®¥ и имеет вид

k= .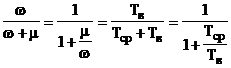

Коэффициент простоя является финальной вероятностью неработоспособного состояния восстанавливаемого объекта с конечным временем восстановления и может быть представлен как среднее время пребывания объекта в этом состоянии в предельном стационарном режиме эксплуатации.

Несмотря на определение коэффициента простоя как асимптотической величины при t®¥, его можно использовать при любых конечных значениях времени t, для которых

|k(t)-k|<e,

где e - заданная погрешность (например, e=0,01).

ПОВЫШЕНИЕ НАДЕЖНОСТИ МАШИН

Срок службы многих видов машин исчисляется десятками лет. Затраты средств, труда и материалов на поддержание и восстановление работоспособного и исправного состояния машины за полный срок службы в 5-10 и более раз превышают затраты на ее изготовление. Например, стоимость ремонта погрузчиков до капитального ремонта в среднем превышает его первоначальную стоимость в 4-5 раз.

Если долговечность машин недостаточна, их изготавливают в большем количестве, чем нужно, что ведет:

- к перерасходу металла,

- к излишкам производственных мощностей,

- к завышению расходов на ремонт и эксплуатацию.

Следовательно, повышение надежности объектов - важная народнохозяйственная задача.

Особенностью надежности является ее связь со всеми этапами создания и эксплуатации объекта от момента формирования и обоснования идеи создания объекта до его списания и сдачи в ремонт.

Надежность закладывается при разработке объекта и определяется:

- конструкцией объекта и его узлов;

- уровнем стандартизации и унификации;

- применяемыми материалами;

- термообработкой;

- методами защиты от вредных воздействий;

- приспособленностью к обслуживанию и ремонту и др.

Надежность обеспечивается при изготовлении и зависит от уровня технологического процесса, который характеризует:

- качество изготовленных деталей;

- качество сборки объекта и его узлов;

- методы контроля и испытания объектов;

- трудоемкость;

- материалоемкость;

- себестоимость изготовления и др.

Надежность реализуется и поддерживается при эксплуатации, хранении и транспортировании. Надежность проявляется только при использовании объекта и зависит:

- от условий и методов эксплуатации;

- от режимов работы;

- от методов технического обслуживания и других эксплуатационных факторов.

Надежность восстанавливается при ремонте. Эффективность восстановления надежности объекта определяется принятой системой ремонта (ППР и СТОИР) и ремонтопригодностью объекта.

Высокий уровень надежности достижим только при высоком уровне качества каждого этапа создания и использования объекта. Нельзя компенсировать недоработки предыдущего этапа на последующем этапе.