Вероятности состояний системы

Важнейшими характеристиками поведения системы являются вероятности состояний системы.

Физическая система S со множеством состояний S₁,S₂,...,S_i,..., S_j,...,S_n в любой момент времени t может быть в одном из этих состояний с вероятностями

P₁(t),P₂(t),...,P_i(t),...,P_j(t),…,P_n(t), (66)

которые называются вероятностями состояний системы. Здесь P_i(t) при i= 1,2,...,n - вероятность того, что система S находится в состоянии S_i в момент времени t, т.е.

P_i(t)=P{S(t)=S_i}.

Сумма всех вероятностей состояний системы для любого момента времени равна единице:

P₁(t)+P₂(t)+...+P_i(t)+...+P_j(t)+...+P_n(t)= .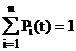

Совокупность вероятностей состояний (66) не является исчерпывающей характеристикой процесса. Полное представление о случайном процессе в системе дают зависимости от времени вероятностей состояний системы, которые могут быть получены из решения системы линейных дифференциальных уравнений.

Дифференциальные уравнения вероятностей состояний

Дифференциальные уравнения вероятностей состояний системы в общем случае (уравнения Колмогорова) имеют вид

.

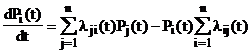Интенсивности потоков l_ij(t) могут быть зависящими от времени и не зависящими от него.

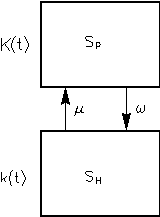
Дифференциальные уравнения составляют по размеченному графу состояний системы (рис. 36) и следующему правилу. Производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное, минус сумма всех потоков вероятности, идущих из данного состояния в другие. Рис. 36. Граф. состояний

Потоком вероятности перехода объекта:

системы из состояния S_i в состояние Sp - работоспособное сос-

S_j называется величина l_ij(t)P_i. тояние объекта (системы);

Отсюда дифференциальные ура- Sн - неработоспособное

внения: состояние объекта

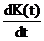=mk(t)-wK(t); (67)

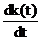=wK(t)-mk(t), (68)

где w - интенсивность потока отказов; m - интенсивность потока восстановлений.

Сумма всех вероятностей состояний объекта для любого момента времени равна единице, т.е. K(t)+k(t)=1.

Общее решение дифференциального уравнения (67) вероятности работоспособного состояния объекта называется функцией готовности и имеет вид

K(t)=C exp(-(w+m)t)+ 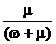. (69)

Общее решение дифференциального уравнения (67) вероятности неработоспособного состояния объекта называется функцией простоя и имеет вид:

k(t)=C exp(-(w+m)t)+ 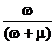. (70)

Произвольная постоянная С определяется из начальных условий, зависящих от того, работоспособен или неработоспособен объект в момент времени t=0:

К_р(0)=1; k_р(0)=0 - при работоспособном состоянии объекта,

К_н(0)=0; k_н(0)=1 - при неработоспособном состоянии объекта.

Готовность объекта

Функция готовности объекта

Функция готовности определяет вероятность работоспособного состояния объекта в произвольный момент времени.

Эта функция является решением дифференциального уравнения вероятности работоспособного состояния объекта:

- для работоспособного состояния объекта в момент времени t=0 из уравнения (69) находим К_р(0)=1 и С= 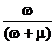, а функция готовности примет вид (рис. 37)

K_p(t)= 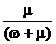+ 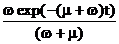=K+k exp(-(w+m)t); (71)

- для неработоспособного состояния объекта в момент времени t=0, K_н(0)=0 и из формулы (69) находим C= 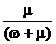, а функция готовности примет вид (см. рис. 37)

K_н(t)=k(t)= 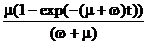=K(1-(w+m)t)), (72)

Функция готовности слагается из двух составляющих - переходной и установившейся (постоянной).

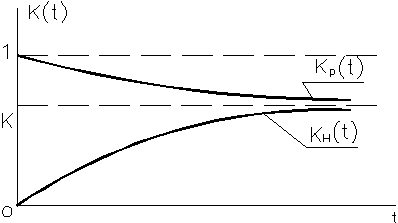Установившееся значение функции готовности, являющееся асимптотой, называется коэффициентом готовности и не зависит от состояния объекта в начальный момент времени. Иначе функцию готовности называют нестационарным коэффициентом готовности.

Рис. 37. Функция готовности

Функция готовности зависит и от показателя w - безотказности, и от показателя m - восстанавливаемости объекта. Значит, функция готовности является комплексным показателем надежности, характеризующим два свойства - безотказность и восстанавливаемость (ремонтопригодность).

Функция простоя

Функция простоя определяет вероятность неработоспособного состояния объекта в произвольный момент времени. Эта функция - решение дифференциального уравнения вероятности неработоспособного состояния объекта:

- для работоспособного состояния объекта в момент t=0 и k_p(t)=0 из формулы (70) находим C= 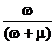, а функция простоя примет вид (рис. 38)

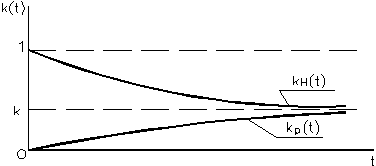k_р(t)= 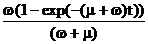=k(1-exp(-(w+m)t)); (73)

Рис. 38. Функция простоя

- для неработоспособного состояния объекта в момент t=0 и k_н(0)=1 из формулы (28) находим С= 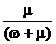, а функция простоя примет вид (см. рис. 38)

k_н(t)= 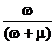+ 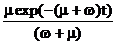=k+K exp(-(w+m)t). (74)

Функция простоя слагается из двух составляющих - переходной и установившейся (постоянной).

Установившееся значение функции простоя, являющееся асимптотой, называется коэффициентом простоя и не зависит от состояния объекта в начальный момент времени. Иначе функция простоя называется нестационарным коэффициентом простоя.

Функция простоя зависит и от показателя w - безотказности, и от показателя m - восстанавливаемости объекта. Таким образом, функция простоя является комплексным показателем надежности, характеризующим два свойства - безотказность и восстанавливаемость (ремонтопригодность).