Определение интегральной и дополнения интегральной функции распределения по известной дифференциальной функции

Для определения интегральной функции распределения по известной дифференциальной функции производим интегрирование функции f(x):

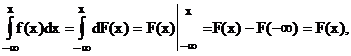
то есть

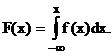(16)

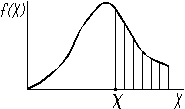Геометрически интегральная функция равна площади криволинейной трапеции F(x)=S_{кр.трап.}, ограниченной осью х и графиком дифференциальной функции f(x), левее точки х (рис. 12).

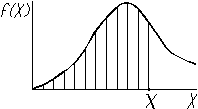Рис. 12. Определение интеграль- Рис. 13. Определение дополне-

ной функции ния интегральной функции

Дополнение интегральной функции по формулам (8) и (16) определяется так:

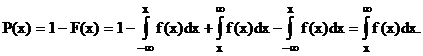
Геометрически дополнение интегральной функции равно площади криволинейной трапеции P(x)=S_{кр.трап.}, ограниченной осью х и графиком функции, правее точки х (рис. 13).

Вероятность появления события на интервале,

Следующем за интервалом, на котором событие

Не появлялось

Вероятность появления события на интервале, следующем за интервалом, на котором событие не появлялось, является условной вероятностью.

Для определения найдем сначала условную вероятность P_t(Dt) непоявления события на интервале Dt при условии непоявления события на предыдущем интервале t (рис. 14).

По теореме умножения вероятностей зависимых событий можно записать

P(t+Dt)=P(t)P_t(Dt), (17)

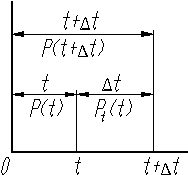где P(t) - безусловная вероятность непоявления события на интервале t; P(t+ Dt) - безусловная вероятность непоявления события на интервале t+Dt, то есть вероятность одновременного непоявления событий и на интервале t, и на интервале Dt. Условная вероятность непоявления события (отказа, восстановления работоспособности) на интервале Dt

при условии непоявления события Рис.14. Интервалы времени

на предыдущем интервале t

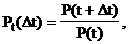(18)

то есть равна отношению вероятностей непоявления события в конце и в начале рассматриваемого интервала времени Dt.

Условная вероятность появления события (отказа, восстановления работоспособности) на интервале Dt при условии непоявления события на предыдущем интервале t

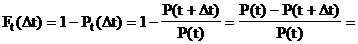
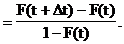(19)

Интенсивность событий

Интенсивность событий (отказов, восстановления работоспособности) - функция l(t), определяющая вероятность появления события в единицу времени в момент t при условии, что событие не появилось до момента t.

Интенсивностью событий является плотность вероятности появления события в момент t при условии, что событие не появлялось до момента t.

Условная вероятность появления события в единицу времени на интервале Dt из формулы (19) равна

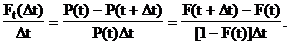
Интенсивность событий получается в результате перехода в уравнении к пределу при Dt®0

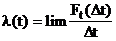
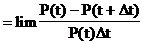
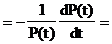
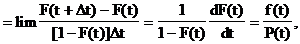
то есть

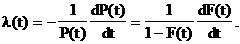(20)

Интенсивность событий по статистической информации определяется как отношение числа объектов, отказавших в единицу времени, к числу объектов, работоспособных в данный момент времени:

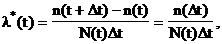
где Dt - интервал времени от t до t+Dt; n(Dt) - число объектов, отказавших в интервале времени Dt; N(t) - число объектов, работоспособных в момент времени t.

Для определения вероятности появления событий через их интенсивность производим интегрирование. Из уравнения (20) имеем

-l(t)dt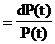

интегрируем его:

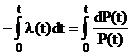=lnP(t)-lnP(0)=lnP(t).

Откуда

P(t)= 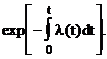(21)