Глава 4. Теория линейной корреляции

Глава 4. Теория линейной корреляции

Функциональная, статистическая и корреляционная зависимости

Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Рассмотрим сначала зависимость Y от одной случайной (или неслучайной) величины X, а затем от нескольких величин.

Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.

Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов, причем среди них могут быть и общие для обеих величин. В этом случае возникает статистическая зависимость.

Например, если Y зависит от случайных факторов Z₁, Z₂, V₁, V₂, a X зависит от случайных факторов Z₁, Z₂, U₁,то между Y и X имеется статистическая зависимость, так как среди случайных факторов есть общие, а именно: Z_lи Z₂.

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.

Приведем пример случайной величины Y, которая не связана с величиной X функционально, а связана корреляционно. Пусть Y – урожай зерна, X – количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, то есть Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и другие). Вместе с тем, как показывает опыт, среднийурожай является функцией от количества удобрений, то есть Y связан с X корреляционной зависимостью.

Пример.

Y	X
0.4 0.6 0.8	–	–	–	–
					n=60

В первой строке таблицы указаны наблюдаемые значения (10; 20; 30; 40) признака X, а в первом столбце – наблюдаемые значения (0,4; 0,6; 0,8) признака Y. На пересечении строк и столбцов находятся частоты п_ху наблюдаемых пар значений признаков. Например, частота 5 указывает, что пара чисел (10; 0,4) наблюдалась 5 раз. Все частоты помещены в прямоугольнике, стороны которого проведены жирными отрезками. Черточка означает, что соответственная пара чисел, например (20; 0,4), не наблюдалась.

В последнем столбце записаны суммы частот строк. Например, сумма частот первой строки «жирного» прямоугольника равна п_у = 5 + 7 + .14 = 26; это число указывает, что значение признака Y, равное 0,4 (в сочетании с различными значениями признака X), наблюдалось 26 раз.

В последней строке записаны суммы частот столбцов. Например, число 8 указывает, что значение призрака X, равное 10 (в сочетании с различными значениями признака Y), наблюдалось 8 раз.

В клетке, расположенной в нижнем правом углу таблицы, помещена сумма всех частот (общее число всех наблюдений n). Очевидно, 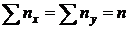. В нашем примере

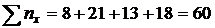и .

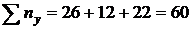4.5. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным

Ранее для определения параметров уравнения прямой линии регрессии Y на X была получена система уравнений

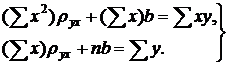(1)

Предполагалось, что значения X и соответствующие им значения Y наблюдались по одному разу. Теперь же допустим, что получено большое число данных (практически для удовлетворительной оценки искомых параметров должно быть хотя бы 50 наблюдений), среди них есть повторяющиеся, и они сгруппированы в виде корреляционной таблицы. Запишем систему (1) так, чтобы она отражала данные корреляционной таблицы. Воспользуемся тождествами:

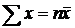(следствие из );

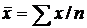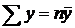(следствие из );

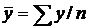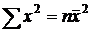(следствие из ),

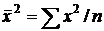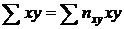(учтено, что пара чисел (х, у)наблюдалась п_ху раз)

Подставив правые части тождеств в систему (1) и сократив обе части второго уравнения на п, получим

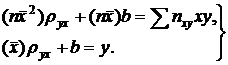(2)

Решив эту систему, найдем параметры r_ху и b и, следовательно, искомое уравнение

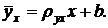(3)

Однако более целесообразно, введя новую величину – выборочный коэффициент корреляции, написать уравнение регрессии в ином виде. Сделаем это. Найдем b из второго уравнения (2):

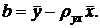
Подставив правую часть этого равенства в уравнение (3), получим

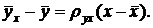(4)

Найдем из системы (1) коэффициент регрессии, учитывая, что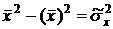

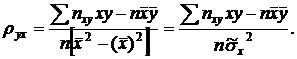
Умножим обе части равенства на дробь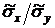

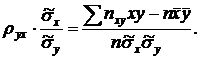(5)

Обозначим правую часть равенства через r_B и назовем ее выборочным коэффициентом корреляции

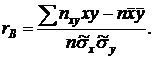
Подставим r_B в (5):

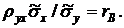
Отсюда

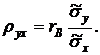
Подставив правую часть этого равенства в (4), окончательно получим выборочное уравнение прямой линии регрессии Y на X вида

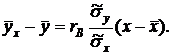
Замечание 1. Аналогично находят выборочное уравнение прямой линии регрессии X на Y вида

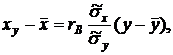
где .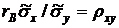

Замечание 2. Уравнения выборочной прямой регрессии можно записать в более симметричной форме:

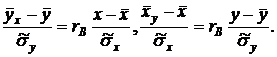
Замечание 3. Можно показать, используя метод моментов, что выборочный коэффициент корреляции является оценкой теоретического коэффициента корреляции

Глава 4. Теория линейной корреляции