Данные, необходимые для расчета и графического изображения шкалы регрессии

a. коэффициент регрессии — R_у/х;

b. уравнение регрессии — у = М_у + R_у/х (х-М_x);

c. сигма регрессии — σ_Rx/y

Стандартная ошибка является оценкой среднего квадратичного отклонения коэффициента регрессии от его истинного значения. Позволяет получить некоторое представление о форме функции плотности вероятности, однако не несёт информации о том, находится ли полученная оценка в середине распределения (т.е. является точной) или в его «хвосте» (т.е. является относительно неточной).

проверке гипотезы H0 остатистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфактопределяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

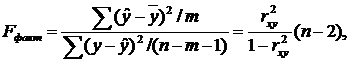
где n – число единиц совокупности;

m – число параметров при переменных x.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если Fтабл< Fфакт, то H0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл> Fфакт, то H0 – гипотеза не отклоняется и признается статистическая незначимость, надежность уравнения регрессии.

2. t-критерий Стьюдента используется для оценки статистической значимости коэффициентов регрессии и коэффициента корреляции.

В качестве основной гипотезы вы­двигают гипотезу H0 о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактиче­ским) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (ко­торые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).

Табличное значение оп­ределяется в зависимости от уровня значимости (a) и числа степеней свободы, которое в случае линейной парной рег­рессии равно (n-2) , n - число наблюдений.

Если фактическое значение t-критерия больше таб­личного (по модулю), то считают, что с вероятностью (1-a) параметр регрессии (ко­эффициент корреляции) значимо отличается от нуля.

Если фактическое значение t-критерия меньше таб­личного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр регрессии (коэффициент корреля­ции) незначимо отличается от нуля при уровне значимости a.

Фактические значения t-критерия определяются по формулам:

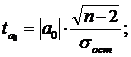
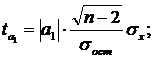
где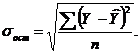

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

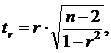
где r - оценка коэффициента корреляции, полученная по наблюдаемым данным. tтабл остается прежним.

3. Адекватность регрессионной модели оценим с помощью средней ошибки аппроксимации – среднее отклонение расчетных значений от фактических:

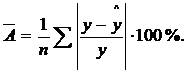
Допустимый предел значений 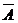– не более 8-10%.