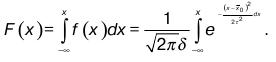Выравнивание вариационных рядов. Теоретические распределения. Распределения Гаусса и Пуассона.
Практически все ряды динамики экономических показателей на графике имеют форму кривой, ломаной линии с подъемами и снижениями. Во многих случаях по фактическим данным ряда динамики и по графику трудно определить даже общую тенденцию развития. Но статистика должна не только определить общую тенденцию развития явления (рост или снижение), но и дать количественные (цифровые) характеристики развития.
Тенденции развития явлений изучают методами выравнивания рядов динамики:
§ Метод укрупнения интервалов
§ Метод скользящей средней
§ Метод аналитического выравнивания
Метод укрупнения интервалов времени основан на исчислении средних величин за укрупненные периоды времени. Цель — абстрагироваться от влияния случайных факторов, взаимопогасить их влияние в отдельные годы.
Метод скользящей средней также основан на исчислении средних величин за укрупненные периоды времени. Цель та же — абстрагироваться от влияния случайных факторов, взаимопогасить их влияние в отдельные годы. Но метод расчета другой.
Метод аналитического выравнивания основан на вычислении значений выравненного ряда по соответствующим математическим формулам. вычисления по уравнению прямой линии:
Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов (значений признака). Теоретическое распределение может быть выражено аналитически – формулой, которая связывает частоты вариационного ряда и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения.
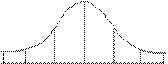
График нормального распределения имеет форму колоколообразной кривой, симметричной относительно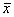 
, концы которой асимптотически приближаются к оси абсцисс. Она имеет точки перегиба, абсциссы которых находятся на расстоянии s от центра симметрии. Эта кривая выражается уравнением:
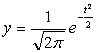
где у – ордината кривой нормального распределения;
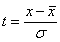- нормированные отклонения.
-2s -s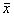 
+s +2s
Рис. Кривая нормального распределения
Закон Пуассона. Другое название его – закон ра-определения редких событий. Закон Пуассона (З. П.) применяется в тех случаях, когда маловероятно, и поэтому применение Б/З/Р нецелесообразно.
Достоинствами закона являются: удобство при вычислении, возможность вычислить вероятность в заданном промежутке времени, возможность замены времени другой непрерывной величиной, например, линейными размерами.
Закон Пуассона имеет следующий вид:
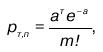
и читается следующим образом: вероятность появления события А в m раз при n независимых испытаниях выражается формулой вида (59), где а = пр – среднее значение p(A), причем а является единственным параметром в законе Пуассона.
Закон нормального распределения (закон Гаусса). Практика неуклонно подтверждает, что закону Гаусса с достаточным приближением подчиняются законы распределения ошибок при измерениях самых различных параметров: от линейных и угловых размеров до характеристик основных механических свойств стали.
Плотность вероятности закона нормального распределения (в дальнейшем Н. Р.) имеет вид
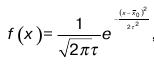
где x0 – среднее значение случайной величины;
? – среднее квадратическое отклонение той же случайной величины;
e = 2,1783... – основание натурального логарифма;
Ж – параметр, который удовлетворяет условию.
Причина широкого применения закона нормального распределения теоретически определяется теоремой Ляпунова.
При известных Х0 и ? ординаты кривой функции f(x) можно вычислить по формуле
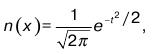
где t – нормированная переменная,
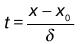
(t) плотность вероятности z. Если подставить z и (t) в формулу, то следует:
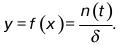
Кривую З.Н.Р. часто называют кривой Гаусса, этот закон описывает очень многие явления в природе.
