Графическое изображение вариационных рядов: полигон, гистограмма, кумулята, кривая Лоренца.
Основные понятия статистики. Статистическое наблюдение. Ошибки наблюдения.
Статистика- это планомерный и систематический учет массовых, общественных явлений, которые осуществляются государственными статистическими органами и дает числовое выражение в проявляющимися закономерностями.Методы статистики: . Массовое статистическое наблюдение- т.е. сбор первичных данных об изучаемых объектах. . Сводка и группировка – представляет собой разделение совокупности данных полученных на этапе наблюдения на однородные группы по одному или нескольким признакам. . Вычисление обобщающих статистических показателей (абсолютных, относительных, средних, показателей вариаций, динамики, индексов) их анализ.Задача: создание методов сбора и обработки стат данных с целью получения научных и практических выводов.Цели:1) Оценка неизвестной вероятности событий.2)Оценка неизвестной ф-ции распределения.3)Оценка параметров известного распределения.4)Оценка степени зависимости одной величины от другой.5)Проверка статистич гипотез о виде неизвестного закона распред-я.Статистические признаки принято делить на две больших группы: 1) Признаки качественные 2) Признаки количественные Качественные признаки (атрибутивные) – это признак отдельное значение которого выражаются в виде понятий, наименований (токарь, слесарь). Если атрибутивные признаки принимают только одну из двух противоположных значений, их называют Альтернативными. Например пол (мужской, женский) Количественный признак – это признак определяющее значение которого имеют количественные выражения например (рост – 155 см.)Статистическое наблюдение– это начальная стадия экономико-статистических исследований.Оно представляет собой научно-организационную работу по собиранию массовых первичных данных о явлениях и процессах общественной жизни, любое статистическое наблюдение осуществляется с помощью оценки и регистра признаков единой совокупности в соответствии с учетными документами, таким образом полученные данные представляют собой факты которые так или иначе характеризуют явления общественной жизни.Различают две основные формы статистического наблюдения – это отчетность и специальное организационное наблюдение.Отчетность – это такая форма наблюдении при которой предприятие, организация предоставляет в статистические и вышестоящие органы постоянные сведения.Специально-организационное наблюдение - это наблюдение которое организуется со специальной целью на определенную дату для получения данных, которые в силу различных причин не собир. стат. Отчетностью, а также с целью проверки данных статистической отчетности. (перепись населения.)Виды статистического наблюденияразличные по времени рег. Данных и по степени охвата ед.совокупности.По времени рег. Фактов. стат наблюдение может быть непрерывным, периодическим и единовременным.По охвату ед. совокупности выделяют сплошное и несплошное наблюдение.В зависимости от источников и причины возникновения неточностей, допускаемых в процессе статистического наблюдения, обычно выделяют ошибки регистрации и ошибки репрезентативности (представительности).
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения или неправильной их записи. Они имеют место как при сплошном, так и несплошном наблюдении. Ошибки регистрации подразделяются на случайные и систематические.
Ошибки репрезентативности (представительности) свойственны не сплошному наблюдению. Они возникают в результате того, что состав отобранной для обследования части массового явления (части единиц совокупности, выборки) недостаточно полно отображает особенности, сущность всей изучаемой совокупности.
Степенные средние величины.
Средние величины делятся на два больших класса: степенные средние и структурные средние.
Степенные средние:
§ Арифметическая
§ Гармоническая
§ Геометрическая
§ Квадратическая
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Если вариант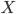 
встречается один раз, расчеты проводим по средней простой (например зарплата в 3 тыс.руб. встречается только у одного рабочего), а если вариант повторяется неодинаковое число раз, то есть имеет разные частоты 
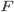(например зарплата в 4 тыс.рублей встречается у пяти работников), то расчет проводим по средней взвешенной.
Дисперсионный анализ.
Дисперсионный анализ (от латинского Dispersio – рассеивание / на английском Analysis Of Variance - ANOVA) применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную.
В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные):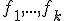 
, а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат.
Основной целью дисперсионного анализа (ANOVA) является исследование значимости различия между средними с помощью сравнения (анализа) дисперсий. Разделение общей дисперсии на несколько источников, позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений).
Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F—критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов.
Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок: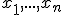 
, которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).
Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным.
Дисперсионный анализ используют, если зависимая переменная измеряется в шкале отношений, интервалов или порядка, а влияющие переменные имеют нечисловую природу (шкала наименований).
Метод наименьших квадратов.
Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.
Примеры
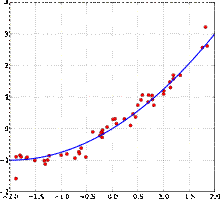
Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения.
Пусть надо решить систему уравнений
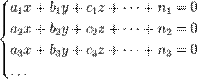 | (1) |
число которых более числа неизвестных x, y,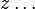 
Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной x и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной y и, сложив почленно, получают второе нормальное уравнение и т. д. Если обозначить для краткости:
 |
то нормальные уравнения представятся в следующем простом виде:
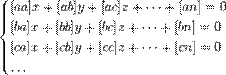 | (2) |
Легко заметить, что коэффициенты нормальных уравнений весьма легко составляются из коэффициентов данных, и притом коэффициент у первой неизвестной во втором уравнении равен коэффициенту у второй неизвестной в первом, коэффициент у первой неизвестной в третьем уравнении равен коэффициенту у третьей неизвестной в первом и т. д
Основные понятия статистики. Статистическое наблюдение. Ошибки наблюдения.
Статистика- это планомерный и систематический учет массовых, общественных явлений, которые осуществляются государственными статистическими органами и дает числовое выражение в проявляющимися закономерностями.Методы статистики: . Массовое статистическое наблюдение- т.е. сбор первичных данных об изучаемых объектах. . Сводка и группировка – представляет собой разделение совокупности данных полученных на этапе наблюдения на однородные группы по одному или нескольким признакам. . Вычисление обобщающих статистических показателей (абсолютных, относительных, средних, показателей вариаций, динамики, индексов) их анализ.Задача: создание методов сбора и обработки стат данных с целью получения научных и практических выводов.Цели:1) Оценка неизвестной вероятности событий.2)Оценка неизвестной ф-ции распределения.3)Оценка параметров известного распределения.4)Оценка степени зависимости одной величины от другой.5)Проверка статистич гипотез о виде неизвестного закона распред-я.Статистические признаки принято делить на две больших группы: 1) Признаки качественные 2) Признаки количественные Качественные признаки (атрибутивные) – это признак отдельное значение которого выражаются в виде понятий, наименований (токарь, слесарь). Если атрибутивные признаки принимают только одну из двух противоположных значений, их называют Альтернативными. Например пол (мужской, женский) Количественный признак – это признак определяющее значение которого имеют количественные выражения например (рост – 155 см.)Статистическое наблюдение– это начальная стадия экономико-статистических исследований.Оно представляет собой научно-организационную работу по собиранию массовых первичных данных о явлениях и процессах общественной жизни, любое статистическое наблюдение осуществляется с помощью оценки и регистра признаков единой совокупности в соответствии с учетными документами, таким образом полученные данные представляют собой факты которые так или иначе характеризуют явления общественной жизни.Различают две основные формы статистического наблюдения – это отчетность и специальное организационное наблюдение.Отчетность – это такая форма наблюдении при которой предприятие, организация предоставляет в статистические и вышестоящие органы постоянные сведения.Специально-организационное наблюдение - это наблюдение которое организуется со специальной целью на определенную дату для получения данных, которые в силу различных причин не собир. стат. Отчетностью, а также с целью проверки данных статистической отчетности. (перепись населения.)Виды статистического наблюденияразличные по времени рег. Данных и по степени охвата ед.совокупности.По времени рег. Фактов. стат наблюдение может быть непрерывным, периодическим и единовременным.По охвату ед. совокупности выделяют сплошное и несплошное наблюдение.В зависимости от источников и причины возникновения неточностей, допускаемых в процессе статистического наблюдения, обычно выделяют ошибки регистрации и ошибки репрезентативности (представительности).
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения или неправильной их записи. Они имеют место как при сплошном, так и несплошном наблюдении. Ошибки регистрации подразделяются на случайные и систематические.
Ошибки репрезентативности (представительности) свойственны не сплошному наблюдению. Они возникают в результате того, что состав отобранной для обследования части массового явления (части единиц совокупности, выборки) недостаточно полно отображает особенности, сущность всей изучаемой совокупности.
Графическое изображение вариационных рядов: полигон, гистограмма, кумулята, кривая Лоренца.
Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными.
Полигон. При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.
Полигон используется для дискретных вариационных рядов.
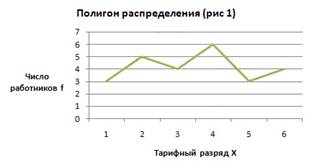
Если значения признака выражены в виде интервалов, то такой ряд называется интервальным. Интервальные рядыраспределения изображают графически в виде гистограммы или кумуляты.
Гистограмма.Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).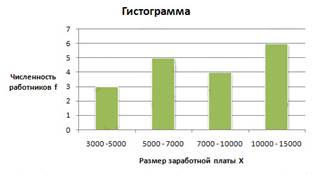 
Кумулята.Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты. Кумулятаили кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости.
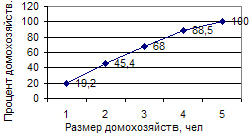
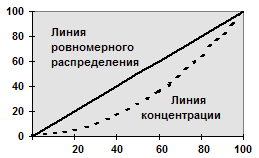
Кривая Лоренца.строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат. Равномерному распределению признака соответствует на графике диагональ квадрата (рис.). При неравномерном распределении график представляет собой вогнутую кривую в зависимости от уровня концентрации признака.
Степенные средние величины.
Средние величины делятся на два больших класса: степенные средние и структурные средние.
Степенные средние:
§ Арифметическая
§ Гармоническая
§ Геометрическая
§ Квадратическая
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Если вариант 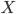встречается один раз, расчеты проводим по средней простой (например зарплата в 3 тыс.руб. встречается только у одного рабочего), а если вариант повторяется неодинаковое число раз, то есть имеет разные частоты 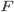(например зарплата в 4 тыс.рублей встречается у пяти работников), то расчет проводим по средней взвешенной.