Характеристики вариационного ряда.
Мода– значение признака, наиболее часто встречающееся в исследуемой совокупности.
Медиана– значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианыв дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.
Пример.Рассчитаем моду и медиану по данным табл. 7.10.
Таблица 7.10
Распределение обуви, проданной коммерческой фирмой в январе 1998 г.
| Размер | 44 и более | Итого | ||||||||||
| Количество проданных пар, % к итогу | ||||||||||||
| Накопленные частоты | - |
В этом ряду распределения мода равна 42. Именно этот размер обуви в январе 1998 г. пользовался наибольшим спросом.
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание продолжается до получения накопленной суммы частот, впервые превышающей половину. В нашем примере сумма частот составила 100, ее половина – 50.
Накопленная сумма частот ряда равна 62. Ей соответствует значение признака, равное 40. Таким образом, 40-й размер обуви является медианным.
Для интервальных вариационных рядов мода определяется по формуле
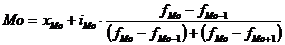 ,
,
где хМо – нижняя граница значения интервала, содержащего моду;
iМо – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+l – частота интервала, следующего за модальным.
Медиана интервального ряда распределения определяется по формуле
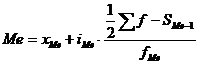 ,
,
где хМе – нижняя граница значения интервала, содержащего медиану;
iMе – величина медианного интервала;
Σf – сумма частот;
SMe-1 – сумма накопленных частот, предшествующих медианному интервалу;
fMe – частота медианного интервала
Пример.Рассчитаем моду и медиану по данным табл. 7.11.
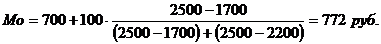
Следовательно, наибольшее число семей имеют среднедушевой доход 772 руб.
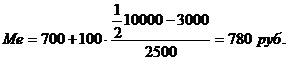
Таким образом, половина семей города имеет среднедушевой доход менее 780 руб., остальные семьи – более 780 руб.
Таблица 7.1
Распределение семей города по размеру среднедушевого дохода
в январе 1998 г.
| Группы семей по размеру дохода, руб. | Число семей | Накопленные частоты | Накопленные частоты, % к итогу |
| До 500 | |||
| 500-600 | |||
| 600-700 | |||
| 700-800 | |||
| 800-900 | |||
| 900-1000 | |||
| Свыше 1000 | |||
| Итого | - | - |
Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на четыре равные части, десять или сто частей. Эти величины называются «квартили», «децили» и «перцентили».
Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q,), отделяющий 1/4 часть совокупности с наименьшими значениями признака, и квартиль верхний (Q3), отсекающий 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% - между Q2 и Q3 и остальные 25% превосходят Q3. Средним квартилем Q2 является медиана.
Для расчета квартилей по интервальному вариационному ряду используют формулы:
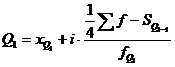 ;
;
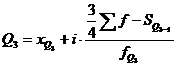 ,
,
где 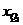 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
– нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
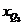 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
– нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
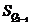 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
– накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
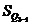 – то же для верхнего квартиля;
– то же для верхнего квартиля;
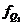 – частота интервала, содержащего нижний квартиль;
– частота интервала, содержащего нижний квартиль;
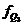 – то же для верхнего квартиля.
– то же для верхнего квартиля.
Рассмотрим расчет нижнего и верхнего квартилей по данным табл. 7.11. Нижний квартиль находится в интервале 600-700, накопленная частота которого равна 30%. Верхний квартиль лежит в интервале 800-900 с накопленной частотой 77%. Поэтому получим:
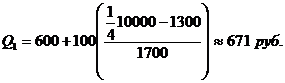
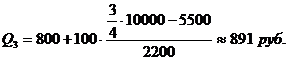
Итак, 25% семей имеют среднедушевой доход менее 671 руб., 25% семей – свыше 891 руб., а остальные имеют доход в пределах 671-891 руб.
Задачи и упражнения
7.1.Распределение студентов одного из факультетов по возрасту характеризуется следующими данными:
| Возраст студентов, лет | Всего | ||||||||
| Число студентов |
Вычислите: а) размах вариации; б) среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; д) относительные показатели вариации возраста студентов.
7.2. Определите среднюю длину пробега автофургона торгово-посреднической фирмы и вычислите все показатели вариации, если известны:
| Длина пробега за один рейс, км | Число рейсов за квартал |
| 30-50 | |
| 50-70 | |
| 70-90 | |
| 90-110 | |
| 110-130 | |
| 130-150 | |
| Всего |
7.3. Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов:
| Количество слов в телеграмме | Число телеграмм |
| Итого |
Рассчитайте абсолютные и относительные показатели вариации.
7.4. Средняя урожайность зерновых культур в двух районах за 1991-1995 гг. характеризуется следующими данными, ц/га:
| 1-й район | |||||
| 2-й район |
Рассчитайте все показатели вариации. Определите, в каком районе урожайность зерновых культур более устойчива.
7.5. Имеются следующие данные выборочного обследования студентов одного из вузов:
| Затраты времени на дорогу до института, ч | Число студентов, % к итогу |
| До 0,5 | |
| 0,5-1,0 | |
| 1,0-1,5 | |
| 1,5-2,0 | |
| Свыше 2,0 | |
| Всего |
Вычислите абсолютные и относительные показатели вариации.
7.6. Имеются следующие данные о распределении скважин в одном из районов бурения по глубине:
| Группы скважин по глубине, м | Число скважин |
| До 500 | |
| 500-1000 | |
| 1000-1500 | |
| 1500-2000 | |
| Свыше 2000 | |
| Итого |
Определите дисперсию и среднее квадратическое отклонение глубины скважин, применяя способ моментов и отсчета от условного нуля.
7.7. Акционерные общества области по среднесписочной численности работающих на 1 января 1998 г. распределялись следующим образом:
| Группы АО по среднесписочной численности работающих | До | 400-600 | 600-800 | 800-1000 | 1000-1200 | 1200-1400 | 1400-1600 | 1600-1800 | Итого |
| Количество АО |
Рассчитайте: а) среднее линейное отклонение; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации.
7.8. По данным о распределении сельских населенных пунктов по числу дворов вычислите общую дисперсию тремя способами: а) обычным; б) упрощенным; в) по формуле 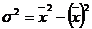 .
.
| Населенные пункты по числу дворов | Число населенных пунктов, % к итогу |
| До 100 | 15,5 |
| 101-200 | 28,6 |
| 201-300 | 21,7 |
| 301-400 | 20,3 |
| Свыше 400 | 13,9 |
| Итого | 100,0 |
7.9. Имеются следующие данные о распределении сотрудников коммерческого банка по среднемесячной заработной плате:
| Группы сотрудников по среднемесячной заработной плате, тыс. руб. | Количество сотрудников, чел. |
| До 3 | |
| 3-4 | |
| 4-5 | |
| 5-6 | |
| 6-7 | |
| 7-8 | |
| 8-9 | |
| 9-10 | |
| Свыше 10 | |
| Итого |
Определите общую дисперсию тремя способами: а) обычным; б) упрощенным; в) по формуле 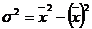 .
.
7.10. Средняя величина признака в совокупности равна 19, а средний квадрат индивидуальных значений этого признака – 397. Определите коэффициент вариации.
7.11. Дисперсия признака равна 9, средний квадрат индивидуальных его значений – 130. Чему равна средняя?
7.12. Средняя величина в совокупности равна 16, среднее квадратическое отклонение – 8. Определите средний квадрат индивидуальных значений этого признака.
7.13. Средний квадрат отклонений индивидуальных значений признака от их средней величины равен 100, а средняя – 15. Определите, чему равен средний квадрат отклонений индивидуальных значений признака от величины, равной 10 и 25.
7.14. Средняя величина признака равна 14, а дисперсия – 60. Определите средний квадрат отклонений вариантов признака от 19.
7.15. Средний квадрат отклонений вариантов признака от произвольной величины равен 300, а сама произвольная величина равна 70 единицам. Определите дисперсию признака, если известно, что средняя величина его варианта равна 80.
7.16. Средний квадрат отклонений вариантов признака от некоторой произвольной величины равен 61. Средняя величина признака больше произвольной величины на 6 единиц и равна 10. Найдите коэффициент вариации.
7.17. Если дисперсия равна 20 000 единицам, а коэффициент вариации – 30%, то каков будет средний квадрат отклонений индивидуальных значений признака от величины, равной 250 единицам?
7.18. По данным таблицы о распределении пряжи по крепости нити вычислите все виды дисперсий. Определите общую дисперсию по правилу сложения дисперсий.
| 1 группа пряжи (менее крепкая) | II группа пряжи (более крепкая) | ||
| Крепость нити, г | Число проб | Крепость нити, г | Число проб |
| 120-130 | 200-210 | ||
| 130-140 | 210-220 | ||
| 140-150 | 220-230 | ||
| 150-160 | 230-240 | ||
| 160-170 | 240-250 | ||
| 170-180 | 250-260 | ||
| 180-190 | 260-270 | ||
| 190-200 |
7.19. Товарооборот по предприятиям общественного питания на одного работника за квартал характеризуется следующими данными:
| Предприятие | Доля предприятий в общей численности работников, % | Товарооборот в расчете на одного работника, тыс. руб. | Дисперсия товарооборота в группе |
| Столовые Кафе, закусочные Рестораны | 3,29 36,00 9,00 |
Определите все виды дисперсий товарооборота предприятий общественного питания.
7.20.Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей в семье | Число семей сотрудников по подразделениям | ||
| первое | второе | третье | |
| - |
Вычислите: а) внутригрупповые дисперсии; б) среднюю из внутригрупповых дисперсий; в) межгрупповую дисперсию; г) общую дисперсию. Проверьте правильность произведения расчетов с помощью правила сложения дисперсий.
7.21.Распределение основных фондов по малым предприятиям отрасли характеризуется следующими данными:
| Группы предприятий по стоимости основных фондов, тыс. руб. | Число предприятий | Основные фонды в среднем на предприятии, тыс. руб. | Групповые дисперсии |
| 12-27 | 1,14 | ||
| 27-42 | 1,09 | ||
| 42-57 | 1,69 | ||
| 57-72 | 1,84 |
Рассчитайте коэффициент детерминации и эмпирическое корреляционное отношение. Сделайте выводы.
7.22. Имеются следующие данные, характеризующие фермерские хозяйства региона:
| Группы хозяйств по стоимости удобрений на 1 га зерновых, тыс. руб. | Число хозяйств | Средняя урожайность, ц/га | Дисперсия урожайности в группе |
| До 1 | 6,25 | ||
| 1-2 | 3,61 | ||
| 2 и более | 8,41 |
Определите коэффициент детерминации и эмпирическое корреляционное отношение при условии, что посевные площади под зерновыми культурами во всех хозяйствах одинаковы. Сделайте выводы.
7.23. Распределение стоимости продукции, предназначенной для экспортных поставок, по цехам предприятия представлено следующими данными:
| Цех | Стоимость всей произведенной продукции, тыс. руб. | В том числе стоимость экспортной продукции, тыс. руб. | |
| Итого | |||
Вычислите: а) среднюю из внутригрупповых, межгрупповую и общую дисперсию дисперсии доли экспортной продукции; б) коэффициент детерминации и эмпирическое корреляционное отношение.
7.24. Имеются данные о распределении семей города по числу детей.
| Число детей | Итого | ||||||
| Число семей, % к итогу |
Используя центральные моменты первых четырех порядков, рассчитайте коэффициенты асимметрии и эксцесса. Сделайте выводы.
7.25. Распределение магазинов по размеру товарооборота за октябрь 1996 г. характеризуется следующими данными:
| Группы магазинов по размеру товарооборота, тыс. руб. | Число магазинов | Группы магазинов по размеру товарооборота, тыс. руб. | Число магазинов |
| До 200 | 500-600 | ||
| 200-300 | 600-700 | ||
| 300-400 | 700-800 | ||
| 400-50 | Свыше 800 | ||
| Итого | - | - |
Определите показатели асимметрии и эксцесса распределения магазинов по размеру товарооборота. Сделайте выводы.
7.26. При исследовании трудовой активности сотрудников организации (отработано человеко-дней за год) получены средние величины и центральные моменты:
| Для мужчин | Для женщин | |
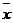 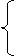 Центральные Центральные 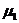 моменты моменты 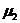 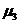 | ||
| -4800 | ||
Используя показатели асимметрии и эксцесса, сравните характер распределения мужчин и женщин по трудовой активности. Сделайте выводы.
7.27. По данным выборочных обследований домашних хозяйств получены средние величины и центральные моменты:
| Для годичного заработка главы семьи | Для среднедушевого дохода семей | |
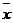 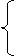 Центральные Центральные 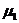 моменты моменты 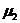 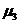 | 11,8 540,0 6800,0 830000,0 |
На основе показателей асимметрии и эксцесса сравните характер распределения домашних хозяйств по годичному заработку главы семьи и среднедушевому доходу. Сделайте выводы.
7.28. Распределение 1000 семей по уровню душевого дохода за месяц характеризуется следующими данными:
| Группы семей по среднедушевому доходу в месяц, руб. | Число семей | Частоты теоретического распределения | |
| нормального | логарифмически-нормального | ||
| до 500 | |||
| 500-600 | |||
| 600-700 | |||
| 700-800 | |||
| 800-900 | |||
| 900-1000 | |||
| 1000-1100 | |||
| 1100-1200 | |||
| 1200-1300 | |||
| 1300 и более | |||
| Итого |
На основе критерия χ2 проверьте, согласуется ли распределение семей по среднедушевому доходу с нормальным или логарифмически-нормальным распределением с вероятностью 0,95.
7.29.По данным задачи 7.28 проверьте близость эмпирического и теоретического распределений с помощью критериев Романовского и Колмогорова.
7.30. Результаты экзамена по теории статистики в одной из студенческих групп представлены в таблице:
| Экзаменационные оценки | Отлично (5) | Хорошо (4) | Удовлетворительно (3) | Неудовлетворительно (2) | Итого |
| Число оценок |
Найдите модальный и медианные баллы успеваемости студентов.
7.31. При изучении качества семян пшеницы было получено следующее распределение семян по проценту всхожести:
| Процент всхожести | Свыше 95 | Итого | |||||||
| Число проб, % к итогу |
Рассчитайте моду и медиану.
7.32. Вычислите моду и медиану количественного состава семей города на основании следующего их распределения по числу совместно проживающих членов семьи:
| Число членов семьи | Итого | ||||||
| Число семей, % к итогу |
7.33. С целью исследования качества деталей на предприятии проверена партия из 100 деталей. Результаты представлены в следующей таблице:
| Группы деталей по весу, г | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | Итого |
| Число деталей |
Определите моду, медиану, квартили и децили.
7.34. По нижеследующим данным вычислите моду, медиану и квартили.
| Группы порций торфа по влажности, % | Число проб | Группы порций торфа по влажности, % | Число проб |
| 20-22 | 26-28 | ||
| 22-24 | 28-30 | ||
| 24-26 | 30-32 | ||
| Итого | - | - |
7.35. Рассчитайте моду, медиану, квартили и децили по данным задачи 7.25.
7.36. Определите моду, медиану, квартили и децили по данным задачи 7.28.
Рекомендации преподавателям
1. Практические занятия.На практических занятиях целесообразно часть времени отвести обсуждению со студентами сущности, назначения и использования каждого из показателей вариации. Особое внимание следует обратить на относительные показатели вариации и разные виды дисперсий, их единство и различия, добиваясь глубокого усвоения студентами их логического содержания. Студенты должны усвоить смысл практического применения таких показателей, в частности при изучении взаимосвязи рядов динамики и выборочного наблюдения.
В результате решения задач студенты должны овладеть способами вычисления того или иного показателя, выработать навыки проведения расчетов, а также усвоить сущность и задачи изучения вариации социально-экономических явлений. Задачи для решения следует выбрать в той последовательности, в какой они даны в этой главе. Небольшие задачи в главе (с 7.10 по 7.17) даны для закрепления понимания взаимосвязи средних величин, разных показателей вариации и их математических свойств. Необходимо, чтобы эти задачи студенты научились решать, не прибегая к вычислениям на бумаге или счетной технике. Когда студенты научатся решать задачи в уме, можно считать, что они достаточно усвоили основной материал темы.
Завершением практических занятий по теме должно быть определение структурных характеристик вариационного ряда и выяснение их смысла. Особое внимание надо обратить на вычисление и экономическую интерпретацию квартилей ряда распределения.
2. Задание для самостоятельной внеаудиторной работы студентов.Задания (два-три) могут быть даны в виде последовательного набора задач в соответствии с построением практических занятий или в виде одной комплексной задачи с условием последовательного ее решения. Можно дать сведения о двух совокупностях крупнейших компаний (приложение 14), предложите провести исследование вариации (давая студентам разные пары взаимосвязанных признаков) в каждой совокупности компаний, затем в целом по обеим совокупностям, а также исследование тесноты связи с определением ее количественной характеристики в виде корреляционного отношения (эмпирического). Выбор типа задания зависит от многих конкретных условий преподавания курса теории статистики. Если время, отведенное учебным планом на курс, ограничено, наиболее целесообразен первый или второй тип задания.
3. Аудиторная контрольная работа.Она должна быть рассчитана на 1-2 ч аудиторной работы (в зависимости от отведенного на курс времени) и содержать последовательный набор небольших задач или одну комплексную задачу, на основе данных которой могут быть рассчитаны разные показатели вариации.
