Построение рядов распределения и их графическое изображение
Ряды могут быть:
§ атрибутивные
§ вариационными (построены по количественному признаку)
Если ряд строится по непрерывному признаку, то он имеет вид интервального вариационного ряда.
Ряды распределения строятся по правилам группировок. При построении интервальных вариационных рядов необходимо добиваться отсутствия малонаполненых и нулевых групп. Следует так же стремиться к получению одновершинного распределения, когда по обе стороны от max частоты наблюдается закономерное уменьшение частот. Если графическое изображение вариационного ряда демонстрирует двухвершинное распределение или многовершинное, следует понять, существуют ли действительно ____________ группы со своими индивидуальными значениями, или же наличие нескольких вершин есть дефект группировки.
Если это дефект группировки, то следует произвести перегруппировку путем уменьшения числа групп. Если отдельные группы объективно существуют в изучаемой совокупности, то их распределение следует изучать отдельно.
| варианты | частоты fi | частости fi’ | накопленные частоты Efi | накопленные частости Efi’ |
| A | ||||
| X1 X2 Xi Xn | f1 f2 fi fn | f1’ f2’ fi’ fn’ | fi f1+f2 f1 +f2 +fi f1’+ f2’ +fi +fn’ | fi’ f1’ +f2’ f1’ +f2’ +fi’ f1’+f2’+fi’ +fn’ |
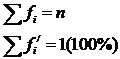
Значение признака в вариационном ряду носит название варианта.
Частота fi показывает, как часто данное значение признака встречается в изучаемой совокупности или сколько единиц совокупности обладают значением признака, указанным в конкретной группе.
Частости f/I или относительные частоты или статистическая вероятность характеризуют долю каждой группы в общей совокупности. Рассчитывается как отношение числа единиц каждой группы к общему числу единиц в совокупности (т.е. как отношение числа единиц благоприятных исходов к общему числу возможных исходов, поэтому и называется статистической вероятностью, т.е. вероятность определенная на основе фактических данных)
Накопленные частоты и частости получают путем последовательного суммирования по группам. Накопленная частота последней группы соответствует частоте совокупности. Накопленная частость в последней группе составляет 1 или 100%.
Построение рядов распределения начинается с ранжирования данных, т.е. распределяют единицы по возрастанию(убыванию) значения признака. Построение ранжированного ряда, а так же графическое изображение рядов распределения позволяют увидеть наличие в совокупности выбросов.
Выбросы – значение показателя, редко отличающегося от основной массы значений показателей совокупности.
Наличие выбросов, как правило, связано с воздействием тех факторов, которые не влияют на формирование значений признака у основной части единиц совокупности, поэтому при анализе рядов распределения выбросы необходимо исключить.
Графическое изображение рядов распределения.
Графическое представление рядов распределения (Р.Р.)
Для графического представления Р.Р. используются след графики: 1 полигон распределения, 2 гистограмма, 3 кумулята
При построение графиков по оси абсцисс или оси х откладываются значения признака или варианты, по оси ординат – частоты или частости
Полигон распределения
Этот график классически используется для изображения вариационного ряда построенного по дискретному признаку. Если полигон распределения стремится к интервальному вариационному ряду то в кач-ве варианта используется значение соответствующее серединам интервала.
РИС
Гистограмма
Данный график используется для изображения интервальных вариационных рядов. Основание столбиков соответствуют величине интервала, а высота частоте по каждому интервалу. На гистограмме можно найти значение моды.
Мода - наиболее часто встречающееся значение признаков совокупности.
РИС
Кумулята
Строиться по накопленным частотам или частостям. При построение графика условно нижней границей 1-ого интервала присваивается 0-я частота, верхней границе частота 1-ого интервала, верхней границы 2-ого интервала соответствует накопленная частота 2-ого интервала и тд. При построение кумуляты распределения можно найти значение медианы.
РИС
