Измерение социальных явлений и процессов. Измерительные шкалы: номинальные, ранговые (порядковые) и интервальные.

Мат.статистика

Измерение социальных явлений и процессов. Измерительные шкалы: номинальные, ранговые (порядковые) и интервальные.

Под измерением в социологическом исследовании понимаетсяпроцедура, с помощью которой объекты измерения, рассматриваемые как носители соответствующих отношений, отображаются в некоторую математическую систему с соответствующими отношениями между элементами. Это процедура приписывания чисел значениям изучаемого признака, целью которой является получение числовой модели исследования.

Под шкалой понимается тот алгоритм, с помощью которого устанавливается соответствие между свойствами социального объекта и свойствами сопоставляемых чисел. В социологии обычно выделяют следующие виды шкал:

Номинальные,

Порядковые (ранговые),

Типы выборок

Выборки делятся на два типа:

- вероятностные

- невероятностные

Вероятностные выборки:

1. Простая вероятностная выборка:

Простая повторная выборка. Использование такой выборки основывается на предположении, что каждый респондент с равной долей вероятности может попасть в выборку. На основе списка генеральной совокупности составляются карточки с номерами респондентов. Они помещаются в колоду, перемешиваются и из них наугад вынимается карточка, записывается номер, потом возвращается обратно. Далее процедура повторяется столько раз, какой объём выборки нам необходим. Минус: повторение единиц отбора.

Простая бесповторная выборка. Процедура построения выборки такая же, только карточки с номерами респондентов не возвращаются обратно в колоду.

2.Систематическая вероятностная выборка. Является упрощенным вариантом простой вероятностной выборки. На основе списка генеральной совокупности через определённый интервал (К) отбираются респонденты. Величина K определяется случайно. Наиболее достоверный результат достигается при однородной генеральной совокупности, иначе возможны совпадение величины шага и каких-то внутренних циклических закономерностей выборки (смешение выборки). Минусы: такие же как и в простой вероятностной выборке.

3.Серийная (гнездовая) выборка. Единицы отбора представляют собой статистические серии (семья, школа, бригада и т.п.). Отобранные элементы подвергаются сплошному обследованию. Отбор статистических единиц может быть организован по типу случайной или систематической выборки. Минус: Возможность большей однородности, чем в генеральной совокупности.

4.Районированная выборка. В случае неоднородной генеральной совокупности, прежде, чем использовать вероятностную выборку с любой техникой отбора, рекомендуется разделить генеральную совокупность на однородные части, такая выборка называется районированной. Группами районирования могут выступать как естественные образования (например, районы города), так и любой признак, заложенный в основу исследования. Признак, на основе которого осуществляется разделение, называется признаком расслоения и районирования.

5.«Удобная» выборка. Процедура «удобной» выборки состоит в установлении контактов с «удобными» единицами выборки - с группой студентов, спортивной командой, с друзьями и соседями. Если необходимо получить информацию о реакции людей на новую концепцию, такая выборка вполне обоснованна. «Удобную» выборку часто используют для предварительного тестирования анкет.

Невероятностные выборки (отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.):

1.<Квотная выборка – выборка строится как модель, которая воспроизводит структуру генеральной совокупности в виде квот (пропорций) изучаемых признаков. Число элементов выборки с различным сочетанием изучаемых признаков определяется с таким расчётом, чтобы оно соответствовало их доле (пропорции) в генеральной совокупности. Так, например, если генеральная совокупность у нас представлена 5000 человек, из них 2000 женщин и 3000 мужчин, тогда в квотной выборке у нас будут 20 женщин и 30 мужчин, либо 200 женщин и 300 мужчин. Квотированные выборки чаще всего основываются на демографических критериях: пол, возраст, регион, доход, образование и прочих.

Плюсы: обычно такие выборки репрезентативны.

Минусы: применение данного способа построения выборки возможно при наличии достаточно полной информации о генеральной совокупности.

2.Метод снежного кома. Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)

3.Стихийная выборка – выборка так называемого «первого встречного». Часто используется в теле- радио- опросах. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов.

Минусы: невозможно установить какую генеральную совокупность представляют опрошенные, и как следствие – невозможность определить репрезентативность.

4.Маршрутный опрос – часто используется, если единицей изучения является семья. На карте населённого пункта, в котором будет производится опрос, нумеруются все улицы. С помощью таблицы (генератора) случайных чисел отбираются большие числа. Каждое большое число рассматривается как состоящее из 3-х компонентов: номер улицы (2-3 первых числа), номер дома, номер квартиры. Например, число 14832: 14 – это номер улицы на карте, 8 – номер дома, 32 – номер квартиры.

5.Районированная выборка с отбором типичных объектов. Если после районирования из каждой группы отбирается типичный объект, т.е. объект, который по большинству изучаемых в исследовании характеристик приближается к средним показателям, такая выборка называется районированной с отбором типичных объектов.

Способы построения выборки:

1.Рандомизация, или случайный отбор, используется для создания простых случайных выборок. Использование такой выборки основывается на предположении, что каждый член популяции с равной вероятностью может попасть в выборку.

2.Попарный отбор — стратегия построения групп выборки, при котором группы испытуемых составляются из субъектов, эквивалентных по значимым для эксперимента побочным параметрам. Данная стратегия эффективна для экспериментов с использованием экспериментальных и контрольных групп.

3.Многоступенчатый способ построения выборки. При многоступенчатом отборе выборка строится в несколько этапов, причём на каждой стадии меняется единица отбора.

4.Многофазный способ построения выборки – является разновидностью многоступенчатого способа, заключается в том, что из сформированной выборки большего объёма производится новая выборка меньшего объёма, при этом, единица отбора остаётся одной и той же.

5.Комбинированный способ построения выборки – соединение в многоступенчатой выборке различных приёмов отбора.

6) Интервальные оценки неизвестных параметров распределения по выборке. Доверительная вероятность. Доверительные интервалы.

Точечной называется оценка, которая определяется одним числом. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.13.3. Доверительные интервалы для оценки математического ожидания нормального распределения при известном103σ.

Интервальной называется оценка, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок (смысл этих понятий выясняется ниже). Пусть найденная по данным выборки статистическая характеристика Θ∗

служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом

(Θ может быть и случайной величиной). Θ∗

тем точнее определяет параметр Θ,

чем меньше абсолютная величина разности |Θ − Θ∗

|. Другими словами, если

δ > 0 и |Θ − Θ∗

| < δ, то чем меньше δ, тем оценка точнее.

Таким образом, положительное число δ характеризует точность оценки.

Статистические методы не позволяют категорически утверждать, что оценка Θ∗

удовлетворяет неравенству |Θ − Θ∗

| < δ; можно лишь говорить о вероятности γ,

с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки Θ по Θ∗

называют ве-

роятность γ, с которой осуществляется неравенство |Θ − Θ∗

| < δ. Обычно на-

дежность оценки задается наперед, причем в качестве γ берут число, близкое к

единице. Наиболее часто задают надежность, равную 0.95, 0.99 и 0.999.

Пусть вероятность того, что , |Θ − Θ∗

| < δ равна γ

P(|Θ − Θ

∗

| < δ) = γ. (13.5)

Заменив неравенство |Θ − Θ∗

| < δ | равносильным ему двойным неравенством

−δ < Θ − Θ∗< δ, или Θ∗ − δ < Θ < Θ∗ + δ, получим

P(Θ

∗

− δ < Θ < Θ

∗

+ δ) = γ. (13.6)

Это соотношение будем понимать так: вероятность того, что интервал (Θ∗ −

δ, Θ∗ + δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.

Доверительным называют интервал (Θ∗ − δ, Θ∗ + δ), который покрывает неиз-

вестный параметр с заданной надежностью γ.

Интервал (Θ∗ − δ, Θ∗ + δ) имеет случайные концы (они называются довери-

тельными границами).

Уравнение регрессии

Уравнение регрессии выглядит следующим образом: Y=a+b*X

При помощи этого уравнения переменная Y выражается через константу a и угол наклона прямой (или угловой коэффициент) b, умноженный на значение переменной X. Константу a также называют свободным членом, а угловой коэффициент - коэффициентом регрессии или B-коэффициентом. В большинстве случав (если не всегда) наблюдается определенный разброс наблюдений относительно регрессионной прямой. Остаток - это отклонение отдельной точки (наблюдения) от линии регрессии (предсказанного значения).

Закон больших чисел.

Зако́нбольши́хчи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду. Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Слабый закон больших чисел

Пусть есть бесконечная последовательность (последовательное перечисление) одинаково распределённых и некоррелированных случайных величин 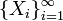, определённых на одном вероятностном пространстве 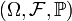То есть их ковариация 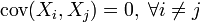Пусть 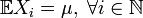Обозначим S_n выборочное среднее первых n членов:

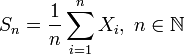
Тогда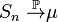

Усиленный закон больших чисел

Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин 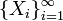определённых на одном вероятностном пространстве 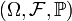.Пусть 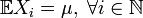.Обозначим выборочное среднее первых членов:

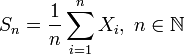
Тогда 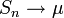почти наверное.

Мат.статистика

Измерение социальных явлений и процессов. Измерительные шкалы: номинальные, ранговые (порядковые) и интервальные.

Под измерением в социологическом исследовании понимаетсяпроцедура, с помощью которой объекты измерения, рассматриваемые как носители соответствующих отношений, отображаются в некоторую математическую систему с соответствующими отношениями между элементами. Это процедура приписывания чисел значениям изучаемого признака, целью которой является получение числовой модели исследования.

Под шкалой понимается тот алгоритм, с помощью которого устанавливается соответствие между свойствами социального объекта и свойствами сопоставляемых чисел. В социологии обычно выделяют следующие виды шкал:

Номинальные,

Порядковые (ранговые),