Индексные метод в статистике

Индекс - это обобщающий показатель, используемый для сравнения двух совокупностей, состоящих из элементов, непосредственно не поддающихся суммированию.

Назначение индексов:

- обеспечить сравнение элементов двух совокупностей

- провести анализ изменения одного показателя под влиянием изменения других показателей.

Индексный метод имеет свою символику:

q - количество (объем) какого-либо продукта в натуральном выражении

p - цена единицы товара

z - себестоимость единицы продукции

t - затраты времени на производство единицы продукции (трудоемкость)

w - выработка продукции в стоимостном выражении на одного работника в единицу времени

v - выработка продукции в натуральном выражении на одного работника или в единицу времени

pq - общая стоимость произведенной продукции или общая стоимость проданных товаров или услуг (товарооборот, выручка)

zq - затраты на производство всей продукции

1 - для сравниваемых (текущих) периодов

0 - для периодов, с которыми производится сравнение

По степени охвата элементов совокупности различают индексы:

- индивидуальные

- групповые

- общие

Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления.

Применение индивидуальных индексов ограничено, т.к. их вычисление требует высокой степени однородности сравниваемых величин.(хлеб разных сортов)

Общие индексы отражают изменение всех элементов сложного явления.

При этом под сложным явлением подразумевается такая статистическая совокупность , отдельные элементы которой непосредственно не подлежат суммированию.

Если индексы не охватывают все элементы сложного явления , а лишь их часть , то их называют групповыми или субиндексами (индекс продукции по отдельным отраслям промышленности).

Общие индексы могут быть построены двумя способами:

- как агрегатные

- как средние из индивидуальных, которые подразделяются на средние арифметические и средние гармонические

Агрегатный индекс является основной формой индекса. Он агрегатный, т.к. его числитель и знаменатель представляют собой набор - "Агрегат" - непосредственно несоизмеримых и не поддающихся суммированию - сумму произведения двух величин, одна из которых меняется (индексируется), а другая - остается неизменной и в числителе и в знаменателе (вес индекса).

Агрегатный способ исчисления общих индексов в статистике является основным наиболее распространенным, вместе с тем применяется и другой способ расчета общих индексов как средних из соответствующих индивидуальных индексов. К исчислению таких средневзвешенных индексов прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если неизвестны количества произведенных отдельных видов продукции в натуральных измерителях, но известны индивидуальные индексы и стоимость продукции базисного периода, можно определить средний арифметический индекс физического объема продукции.

Индексы — обобщающие показатели сравнения во времени и в пространстве не только однотипных (одноименных) явлений, но и совокупностей, состоящих из несоизмеримых элементов.

Методики построения и расчета индексов как для временных, так и для пространственных сравнений одинаковы. Не различаются между собой и методы построения индексов различных явлений. Поэтому рассмотрим расчет на примере индексируемыхцен (р),объемов продаж (производства) (q),товарооборотов (pq). изменяющихся во времени.

Динамика одноименных явлений изучается с помощью индиви­дуальных индексов, которые представляют собой известные от­носительные величины сравнения, динамики или выполнения плана (обязательств):

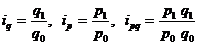
где подстрочное обозначение «О» соответствует уровнюбазисногопериода (с которым сравнивают) или момента времени, «1» — уровнюотчетного (сравниваемого) периода или момента времени.

Изменения совокупностей, состоящих из элементов, непосредст­венно не сопоставимых (например, различных видов продукции), изучают с помощью групповых, или общих, индексов. Последние по методам построения подразделяются на агрегатные индексы и средневзвешенные из индивидуальных индексов.

Формулы агрегатных индексов:

1) физического объема:

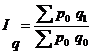
где q- индексируемая величина; р₀ – соизмеритель, или вес, который фиксируется на уровне одного и того же периода. В случае индексов объемных показателей весами являются качественные показатели (цена, себестоимость и др.), зафиксированные на уровне базисного периода.

Разница между числителем и знаменателем индекса

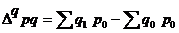
в данном случае означает абсолютное изменение товарооборота (прирост или снижение) за счет изменения физического объема;

2) цен и других качественных показателей:

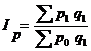- формула Пааше,

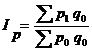- формула Ласпейреса.

где q — объемы (количества) являются весами, взятыми на одина­ковом уровне (отчетном или базисном).

Разница между числителем и знаменателем индексов

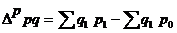или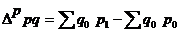

означает:

• в первом случае — абсолютный прирост товарооборота (вы­ручки от продаж) в результате среднего изменения цен или экономию (перерасход) денежных средств населения в результате среднего сни­жения (повышения) цен;

• во втором случае — условный абсолютный прирост товаро­оборота, если бы объемы продаж в отчетном периоде совпали с объ­емами продаж в базисном периоде;

3) товарооборота (выручки от реализации или продаж):

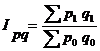
где pq — индексируемое сложное явление, в состав которого входят соизмеримые элементы совокупности. Разница между числителем и знаменателем индекса 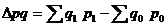составляет абсолютноe изменение товарооборота за счет совместного действия обоих фак­торов: цен на продукцию и ее количества.

Кроме этих форму общие индексы могут быть рассчитаны как средние индексы из индивидуальных:

1) физического объема:

— средний арифметический индекс,

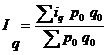
2) цен:

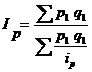- средний гармонический индекс Пааше,

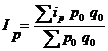- средний арифметический индекс Ласпейреса.

Если индексы качественных показателей построены на основе весов, взятых на уровне отчетного периода (например, по формуле Пааше), то рассмотренные выше агрегатные индексы, а также их элементы взаимосвязаны между собой:

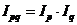(так называемая мультипликативная модель);

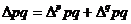(так называемая аддитивная модель).

Если сравнивают друг с другом не два периода (момента), а более, то выделяют цепную и базисную системы индексов.

Цепные и базисные индивидуальные индексы взаимосвязаны между собой:

· произведение цепных индексов равно конечному базисному;

· частное от деления двух смежных базисных индексов равно промежуточному ценному.

Между цепными и базисными общими индексами, построенными на основе постоянных весов, существует взаимосвязь, аналогичная взаимосвязи между индивидуальными индексами.

Индексы, построенные на основе переменных весов, непосредст­венно перемножать и делить нельзя.

Индексный метод широко применяется также для изучения ди­намики средних величин и выявления факторов, влияющих на ди­намику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов. Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризую­щее изменение индексируемого (осредняемого) показателя.

Индекс переменного состава для любых качественных показателей имеет следующий вид:

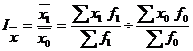
Величина этого индекса характеризует изменение средневзвешенной за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.

Индекс постоянного (фиксированного) состава представляет собой отношение средних взвешенных с одними и теми же весами (при постоянной структуре). Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя (х) у единиц совокупности. В общем виде он может быть записан следующим образом:

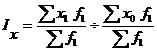
Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:

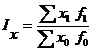
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индек­сируемого показателя и рассчитывается по формуле

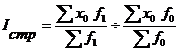
Под структурными изменениями понимается изменение доли от­дельных групп единиц совокупности в общей их численности (d). Система взаимосвязанных индексов при анализе динамики среднего уровня качественного показателя имеет вид

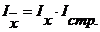
Аналогично приведенным формулам строятся индексы средних уровней: цен, себестоимости продукции, фондоотдачи, производи­тельности труда, оплаты труда и др.