Iii. краткие сведения из теории

СТАТИСТИКА

Методические указания для самостоятельной работы студентов экономических специальностей

ИВАНОВО 2001

Составитель: И.О.ВОЛКОВА

Редактор: О.В.МАКАШИНА

Методические указания разработаны в соответствии с требованиями Государственного стандарта 2000 года и предназначены для студентов экономических специальностей.

Методические указания утверждены на заседании цикловой методической комиссии ФЭУ.

Рецензент:

кафедра экономики и организации предприятия

I. ЦЕЛИ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ

Цель преподавания дисциплины “Статистика” -дать будущим экономистампредставление о принципах изучения массовых явлений и об изменениях в социально-экономических процессах, вооружить их методами построения и анализа основных статистических показателей, а также научить использовать в профессиональной деятельности основные методы обработки и анализа данных наблюдения и эксперимента.

Базой для изучения дисциплины являются знания, полученные студентом при изучении дисциплин: общая экономическая теория, высшая математика, экономика предприятия.

II. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

1.	Предмет и методы статистики. Предмет, метод и основные категории статистики как науки.Организация статистики в РФ и ее задачи.
2.	Статистическое наблюдение. Основные этапы статистического исследования. Программно-методологические и организационные вопросы статистического наблюдения. Формы, виды и способы наблюдения.
3.	Группировка статистических данных и ее роль в анализе информации. Сводка статистических данных. Группировка статистических данных. Классификация группировок. Статистические таблицы. Статистические графики.
4.	Статистические величины. Общие принципы построения статистических показателей. Абсолютные и относительные величины. Средние величины и их виды. Структурные средние - мода и медиана.
5.	Статистическое распределение и его основные характеристики. Вариация признака в совокупности. Основные характеристики и графическое изображение вариационного ряда. Показатели центра распределения. Показатели вариации (колеблемости признака). Моменты распределения. Формы распределения.Критерии согласия.
6.	Выборочное наблюдение. Понятие о выборочном наблюдении. Генеральная и выборочная совокупность.Типы выборки.Ошибки выборки. Численность выборки.
7.	Корреляционная связь и ее статистическое изучение. Статистические методы выявления наличия корреляционной связи между двумя признаками. Измерение степени тесноты корреляционной связи в случае парной зависимости. Уравнение регрессии. Множественная корреляция.
8.	Ряды динамики. Виды рядов динамики.Показатели ряда динамики и методы их определения. Средние характеристики ряда динамики. Выявление и характеристика основной тенденции развития. Понятие сезонной неравномерности и ее характеристика. Корреляционная зависимость между уровнями различных рядов динамики.
9.	Индексный метод в экономико-статистических исследованиях. Общее понятие об индексах. Индексы колическтвенных показателей. Индексы качественных показателей.

III. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Предмет и методы статистики

Статистика, вернее ее методы иссле­дования, широко применяется в различных областях человечес­ких знаний. Различают статистику, занимающуюся изучением социально-экономических явлений, которая относится к циклу общественных наук, и статистику, занимающуюся закономерностями явлений природы, которая относится к наукам естественным.

Настоящий курс посвящен теории статистики социально-эко­номических явлений.

Статистика - общественная наука, которая изуча­ет количественную сторону качественно определенных массо­вых социально-экономических явлений и процессов, их струк­туру и распределение, размещение в пространстве, движение во времени, выявляя действующие количественные зависимо­сти, тенденции и закономерности, причем в конкретных усло­виях места и времени.

Стати­стика как наука исследует не отдельные факты, а массовые социально-экономические явления и процессы,выступающие как множество отдельных факторов, обладающих как индивиду­альными, так и общими признаками.

Предмет и метод составляют сущность любой науки, в том числе и статистики.

Статистика как наука выработала при­емы и способы изучения массовых общественных явлений, зави­сящие от особенностей ее предмета и задач, которые ставятся при его изучении. Приемы и способы, с помощью которых ста­тистика изучает свой предмет, образуют статистическую методо­логию.

Под статистической методологиейпонимается система приемов, способов и методов, направленных на изучение количественных закономерностей, проявляющихся в струк­туре, динамике и взаимосвязях социально-экономических явлений. Задача статистического исследования состоит в полу­чении обобщающих характеристик и выявлении закономернос­тей в общественной жизни в конкретных условиях места и вре­мени, которые проявляются лишь в большой массе явлений че­рез преодоление свойственной ее единичным элементам случай­ности. Важно уяснить, что статистическое исследование состоит из трех стадий: 1) статистическое наблюдение; 2) сводка и груп­пировка результатов наблюдения; 3) анализ полученных обоб­щающих показателей. Все три стадии связаны между собой, и на каждой из них используются специальные методы, объясня­емые содержанием выполняемой работы.

Исходя из характера и основных черт предмета статистики как науки можно сформули­ровать следующие ее задачи. Это изучение:

• уровня и структуры массовых социально-экономических явлений и процессов;

• взаимосвязей массовых социально-экономических явлений и процессов;

• динамики массовых социально-экономических явлений и процессов.

Важно также уяснить, что статистика состоит из ряда отрас­лей, выделившихся в процессе развития, и общая теория стати­стикиявляется методологической основой, ядром всех отрасле­вых статистик, так как она разрабатывает наиболее общие поня­тия, категории, принципы, которые имеют общестатистический смысл, и методы количественного изучения социально-экономи­ческих явлений.

Основное отличие статистики от математики состоит в том, что статистика изучает количественную сторону качественно определенных массо­вых общественных явлений в данных условиях места и вре­мени.При этом качественную определенность единичных явлений обычно определяют сопряженные науки.

Теоретичес­кую основу любой науки, в том числе и статистики, составляют понятия и категории, в совокупности которых выражаются ос­новные принципы данной науки. В статистике к важнейшим категориям и понятиям относятся: совокупность, вариация, при­знак, закономерность.

Статистическая закономерность- это форма проявления причинной связи, выражающаяся в последовательности, регуляр­ности, повторяемости событий с достаточно высокой степенью вероятности, если причины (условия), порождающие события, не изменяются или изменяются незначительно. Статистическая закономерность устанавливается на основе анализа массовых данных. Она возникает в результате действия объективных зако­нов, выражая каузальные отношения.

Так как статистическая закономерность обнаруживается в итоге массового статистического наблюдения, это обусловливает ее взаимосвязь с законом больших чисел.

Сущность закона больших чиселзаключается в том, что в числах, суммирующих результат массовых наблюдений, высту­пают определенные правильности, которые не могут быть обна­ружены на небольшом числе факторов. Закон больших чисел порожден свойствами массовых явлений. Важно помнить, что тенденции и закономерности, вскрытые с помощью закона боль­ших чисел, имеют силу лишь как массовые тенденции, но не как законы для каждого отдельного, индивидуального случая.

Объект статистического исследования (в каждом конкретном случае) в статистике называют статистической совокупностью. Статистическая совокупность -это множество единиц, об­ладающих массовостью, однородностью, определенной целостностью, взаимозависимостью состояния отдельных единиц и наличием вариации.Например, в качестве особых объектов статистического исследования, т. е. статистических совокупнос­тей, может выступать множество коммерческих банков, зареги­стрированных на территории Российской Федерации, множество акционерных обществ, множество граждан какой-либо страны и т. д. Важно помнить, что статистическая совокупность состоит из реально существующих материальных объектов.

Каждый отдельно взятый элемент данного множества назы­вается единицей статистической совокупности.Единицы ста­тистической совокупности характеризуются общими свойствами, именуемыми в статистике признаками,т. е. под качественной однородностью совокупности понимается сходство единиц (объектов, явлений, процессов) по каким-либо существенным признакам, но различающихся по каким-либо другим признакам. Например, из названных совокупностей множество коммерчес­ких банков наряду с качественной определенностью (принадлеж­ностью к разряду кредитных учреждений) обладает различиями по размеру объявленных уставных фондов, численности работа­ющих, сумме активов и т. д.

Качественная определенность совокупности, хотя и имеет объективную основу, устанавливается в каждом конкретном ста­тистическом исследовании в соответствии с его целями и позна­вательными задачами.

Единицы совокупности наряду с общими для всех единиц признаками, обусловливающими качественную определенность совокупности, также обладают индивидуальными особенностя­ми и различиями, отличающими их друг от друга, т. е. существу­ет вариация признаков.Она обусловлена различным сочетани­ем условий, которые определяют развитие элементов множества. Например, уровень производительности труда работников банка определяется его возрастом, квалификацией, отношением к тру­ду и т. д. Именно наличие вариации предопределяет необхо­димость статистики.Необходимо помнить, что вариация при­знака может отражаться статистическим распределением единиц совокупности.

Важно также помнить, что статистика как наука изучает прежде всего количественную сторону общественных явлений и процессов в конкретных условиях места и времени, т. е. предме­том статистикивыступают размеры и количественные соот­ношения социально-экономических явлений, закономернос­ти их связи и развития.

Количественную характеристику статистика выражает через определенного рода числа, которые называются статистичес­кими показателями. Статистический показательотражает результат измерения у единиц совокупности и совокуп­ности в целом.

При изучении данного вопроса важно уяснить, что статисти­ческие совокупности обладают определенными свойствами, носи­телями которых выступают единицы совокупности (явления),обладающие определенными признаками. По форме внешнего выражения признаки делятся на атрибутивные (описательные, качественные) и количественные. Атрибутивные(качественные) признаки не поддаются количественному (числовому) выражению.

Отличие количественныхпризнаков от качественных состоит в том, что первые можно выразить итоговыми значениями, на­пример общий объем перевозок грузов предприятиями транспорта и т. д., вторые - только числом единиц совокупности, например число театров по видам деятельности.

Количественные признаки можно разделить на прерывные (дискретные) и непрерывные.

Статистическое наблюдение

Статистическое наблюдение - это первый этап статистического исследования, представляющая собой научно организованный сбор информации о массовых общественных явлениях и процессах общественной жизни. Статистическим можно назвать лишь такое наблюдение, которое обеспечивает регистрацию устанавливаемых фактов в учетных документах для последующего обобщения.

Статистическое наблюдение может проводиться органами государственной статистики, научно-исследовательскими институтами, экономическими службами банков, бирж, фирм. Оно обязательно должно быть массовым, систематическим, проводиться на научной основе по заранее разработанным плану и программе.

Планомерность статистического наблюдения заключается в том, что оно готовится и проводится по разработанному плану, который входит в план всего статистического исследования и включает вопросы методологии, организации, техники сбора информации, контроля ее достоверности и оформления итоговых результатов.

В плане статистического наблюдения указывается время и место наблюдения. Выбор времени предусматривает решение двух вопросов -установление критического момента (даты) или интервала времени определение срока (периода) наблюдения.

Статистические показатели характеризуют исследуемое явление либо на определенный момент времени, либо за определенный период времени.

Срок (период)наблюдения- это время от начала до окончания сбора сведений, т.е. время, в течение которого производится заполнение статистических формуляров (бланков определенных форм учета и отчетности).

Данные отдельных единиц наблюдения (людей, предприятий и т.д.) должны быть сопоставимы друг с другом, иначе невозможно их последующее обобщение. Сопоставимость данных обеспечивается единством сроков наблюдения (например, численность студентов института определяется на начало учебного года), его программы, методов регистрации данных.

Основной практической целью статистического наблюдения является получение достоверной информации для выявления закономерностей развития явлений и процессов.

Задача наблюдения непосредственно вытекает из задач статистического исследования и предопределяет его программу и формы организации.

В зависимости от цели выбирается объект статистического наблюдения.

Объект статистического наблюдения - совокупность общественных явлений и процессов, которые подлежат данному наблюдению.

Например, при обследовании промышленности объектом наблюдения являются промышленные предприятия.

Определяя объект наблюдения, необходимо точно указать единицу наблюдения.

Единица наблюдения - первичный элемент объекта статистического наблюдения, являющийся носителем признаков, подлежащих регистрации.

Так, например, объектом при переписи населения является совокупность всех жителей страны, а единицей наблюдения – каждый отдельный человек. В том случае, если ставится также задача определения численности и состава домохозяйств, то единицами наблюдения будут являться "человек" и "каждое домохозяйство" (именно эти две единицы устанавливались при проведении микропереписи населения в 1994 г.).

Исходя из содержания объекта, цели и задач статистического наблюдения разрабатывается программа наблюдения.

Программа наблюдения представляет собой перечень показателей, подлежащих регистрации, иными словами, это перечень вопросов, на которые должны быть получены правдивые, достоверные ответы по каждой единице наблюдения .Ее содержание зависит от целей и задач исследования.

Требования к программе наблюдения:

- вопросы должны быть достаточными для разрешения цели и задач исследования

- минимальное число вопросов, необходимое для решения поставленной задачи

- четкая и ясная формулировка вопросов, исключающая двойное толкование

Вопросы программы статистического наблюдения и ответы на них находят отражение в основном инструменте наблюдения - статистическом формуляре (переписной лист, анкета, бланк, и т.д.). Статистический формуляр должен быть удобен для заполнения, чтения, шифровки и машинной обработки данных. К статистическим формулярам составляется инструкция, в которой подробно разъясняется, как следует заполнить статистический формуляр.

Формами статистического наблюдения являются отчетность и специально организованные наблюдения.

Отчетность – предусмотренная действующим законодательством форма организации статистического наблюдения за деятельностью предприятий и организаций, при котором органы государственной статистики получают информацию в виде установленных отчетных документов(форм отчетности),утвержденных Министерством финансов РФ и Госкомстатом РФ, подписанных лицами, ответственными за достоверность сведений.

Решающими являются две формы: баланс и отчет о прибылях и убытках. Финансовый результат, показанный общей суммой в балансе, расшифровывается по составляющим его элементам в отчете прибылях и убытках.

Статистическое наблюдение подразделяется на виды - по времени регистрации данных и по степени охвата единиц наблюдения.

По времени регистрации фактов различают:

· непрерывное, или текущее наблюдение (отчетность, постоянная регистрация данных по мере их возникновения),

· периодическое (регистрация по мере надобности),

· единовременное.

Текущее наблюдение используется, например, в статистике бюджетов населения; примером периодического наблюдения является перепись населения, единовременного - перепись жилого фонда.

По степени охвата единиц совокупности различают сплошное и не сплошное наблюдения.

Сплошным называется такое наблюдение, при котором регистрации подлежат все без исключения единицы изучаемой совокупности.

Несплошным называется такое наблюдение, при котором обследованию подвергаются не все единицы изучаемой совокупности, а только их часть, на основе которой можно получить обобщающую характеристику всей совокупности. Несплошное наблюдение имеет ряд преимуществ перед сплошным: сокращение времени и затрат, более детальная регистрация и т.д.

Несплошное наблюдение подразделяется на:

- способ основного массива,

- монографическое

- выборочное.

Согласно способ наблюдения основного массива сбор данных осуществляется только по тем единицам совокупности, которые дают основной вклад в характеристику изучаемого явления. Часть совокупности, о которой заведомо известно, что она не играет большой роли в характеристике совокупности, исключается из наблюдения.

Например, структуру грузооборота можно изучить, исследовав только крупнейшие транспортные узлы.

Монографическое наблюдение представляет собой подробное описание отдельных единиц совокупности для их углубленного изучения, которое не может быть столь результативным при массовом наблюдении.

Из всех видов несплошного наблюдения в статистической практике наибольшее признание и распространение получило выборочное наблюдение.

Статистическое наблюдение различается и по источникам сведениям или способам регистрации данных:

- непосредственное наблюдение

- документальное наблюдение

- опрос.

Непосредственным является такое наблюдение, при котором сами регистраторы путем замера, взвешивания или подсчета устанавливают факт, подлежащий регистрации, и на этом основании производят записи в формуляре наблюдения.

Документальное наблюдение основывается на различных документах. На документах базируется отчетность.

Опрос - это метод регистрации данных, при котором факты записываются со слов опрашиваемого.

На стадии статистического наблюдения могут возникать ошибки в показателях, обусловленные многими причинами и вызывающие снижение достоверности конечных результатов исследования.

Ошибка регистрации - расхождение между фактическим значением показателя и его значением, полученным при статистическим наблюдении, зафиксированным в статистическом формуляре. Возможны при сплошном и несплошном наблюдении.

Ошибка репрезентативности - расхождение между показателем выборочной совокупности и показателем генеральной совокупности, возникающие вследствие того, что выборочная совокупность недостаточно полно воспроизводит генеральную совокупность. Присущи только несплошному наблюдению.

Таблица 1

Распределение работников строительной фирмы «Скат»

по уровню дохода в январе 1998 г.

Группы работников, по уровню дохода, руб.	Число работников, Чел.	Удельный вес, % к итогу
До 5 000		52,2
5 000 - 7 500		26,1
7 500 - 10 000		13,0
10 000 и более		8,7
Итого		100,0

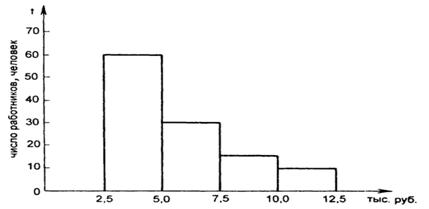
Рис.1.Полигон распределения работников строительной фирмы "Скат"

по уровню дохода в январе 1998 г.

Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абс­цисс откладываются величины интервалов, а частоты изобража­ются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате мы получим гистограмму-график, на ко­тором ряд распределения изображен в виде смежных друг с другом столбиков.

Если середины верхних сторон прямоугольников соединить прямыми, то гистограмма может быть преобразована в полигон распределения (рис. 2).

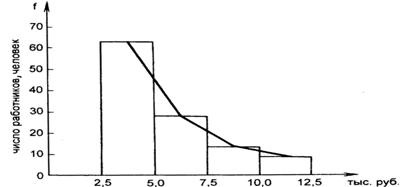
Рис. 3.2.Гистограмма и полигон распределения работников строитель­ной фирмы «Скат» по уровню дохода в январе 1998 г.

Для графического изображения вариационных рядов может использоваться также кумулятивная кривая. При помощи кумуляты(кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показы­вают, сколько единиц совокупности имеют значения признака, не большие, чем рассматриваемое значение.

При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат - накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломанную линию, т.е. кумуляту. Если при графическом изображении вари­ационного ряда в виде кумуляты оси поменять местами, то по­лучим огиву.

Средние величины

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.

Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве.

Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.

Перечисленные средние относятся к классу степенных средних и объединяются общей формулой* (при различных значениях m):

, (3.1)

где 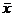- среднее значение исследуемого явления;

m - показатель степени средней;

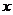- текущее значение (вариант) осредняемого признака;

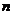- число признаков.

В зависимости от значения показателя степени различают следующие виды степенных средних:

при =-1 - средняя гармоническая ;

при =0 - средняя геометрическая ;

при =1 - средняя арифметическая ;

при =1 – средняя квадратическая ;

при =3 - средняя кубическая .

При использовании одних и тех же исходных данных, чем больше т в формуле (5.1), тем больше значение средней величины:

/ (5.2)

Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется в статистике правилом мажорантности средних.

Средняя арифметическая.

Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Так, например: общий фонд заработной платы – это сумма заработных плат всех работников, валовый сбор урожая – сумма произведенной продукции со всей посевной площади.

Чтобы исчислить среднюю арифметическую нужно сумму всех значений признаков разделить на их число.

Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой служит простая средняя.

Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):

, (5.3)

где , , ..., - индивидуальные значения варьирующего признака (варианты); 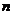- число единиц совокупности.

Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).

Средняя арифметическая взвешенная - средняя сгруппированных величин

, , ..., - вычисляется по формуле:

, (5.4)

где , , ..., - веса (частоты повторения одинаковых признаков);

- сумма произведений величины признаков на их частоты;

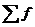- общая численность единиц совокупности.

Если значения осредняемого признака заданы в виде интервалов ("от - до"), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд.

Рассмотрим следующий пример (табл. 5.3).

Таблица 5.3

Распределение рабочих АО по уровню ежемесячной оплаты труда в 1996 г.

Группы рабочих по оплате труда, тыс. руб.	Число рабочих, чел.	Середина интервала, тыс. руб.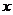
До 500 500-600 600-700 700-800 800-900 900 и более
Итого		-

При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в -интервале.

После того как найдены середины интервалов, вычисления делают также, как и в дискретном ряду, - варианты умножают на частоты (веса) и сумму произведений делят на сумму частот (весов), тыс. руб.:

.

Итак, средний уровень оплаты труда рабочих АО составляет 729 тыс. руб. в месяц.

Средняя гармоническая

Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака 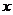и их частоты .

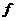Когда статистическая информация не содержит частот 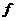по отдельным вариантам 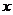совокупности, а представлена как их произведение , применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим , откуда . Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся Данным 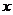и можно было исчислить среднюю. В формулу средней арифметической взвешенной (5.4) вместо подставим , вместо 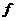- отношение и получим формулу средней гармонической взвешенной.

. (5.9)

Из формулы (5.9) видно, что средняя гармоническая - средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужна определить веса отдельных значений признака, скрытые в весах средней гармонической.

Например, по данным (табл. 5.5) требуется определить среднюю цену 1 кг картофеля.

Таблица 5.5

Цена и выручка от реализации по трем коммерческим магазинам в октябре 1996 г.

Номер магазина	Цена картофеля, руб/кг,	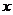Выручка от реализации, млн. руб.,	Частота (количество реализованных едениц), кг,
1-й 2-й 3-й
Итого	-

Расчет средней цены выражается соотношением:

.

В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:

, (5.10)

где - отдельные варианты обратного признака, встречающиеся по одному разу; 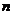- число вариантов.

Средняя геометрическая

Применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется извлечением корня степени 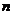из произведений отдельных значений - вариантов признака :

,

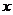где 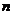- число вариантов; П - знак произведения.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Структурные средние

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода - значение случайной величины, встречающееся с наибольшей вероятностью, в дискретном вариационном ряду - вариант, имеющий наибольшую частоту.

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:

, (5.16)

где - нижняя граница модального интервала; - модальный интервал; , , - частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно).

Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п.

Медиана - это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.

Пусть ряд состоит из показателей заработной платы 9 рабочих, тыс. руб. в месяц (в 1996 г.):

630, 650, 680, 690, 700, 710, 720, 730, 750.

Номер медианы для нечетного объема вычисляется по формуле:

,

где 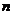- число членов ряда.

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака 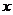. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:

, (5.17)

где - нижняя граница медианного интервала; - медианный интервал; - половина от общего числа наблюдений; - сумма наблюдений, накопленная до начала медианного интервала, - число наблюдений в медианном интервале.

Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.

Правило сложения дисперсий

Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическ<