Средние показатели анализа ряда динамики
| Показатель | Формула расчета | Характеристика показателя |
| Средний уровень ряда | - интервальный ряд с равноотстоящими уровнями 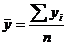 - интервальный ряд с неравноотстоящими уровнями - интервальный ряд с неравноотстоящими уровнями  - моментный ряд с равноотстоящими уровнями - моментный ряд с равноотстоящими уровнями 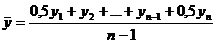 - моментный ряд с неравноотстоящими уровнями - моментный ряд с неравноотстоящими уровнями 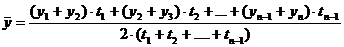 | Показывает усредненную величину изменения ряда динамики. |
| Средний абсолютный прирост | - по цепной системе 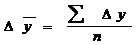 - по базисной системе - по базисной системе 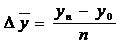 | Показывает, на сколько единиц в среднем происходило увеличение (снижение) анализируемого показателя в единицу времени. |
| Средний коэффициент роста | - по цепной системе 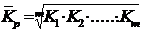 - по базисной системе - по базисной системе 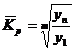 | Показывает среднюю относительную скорость изменения уровня явления (в долях единицы – коэффициент роста, в процентах – темп роста). |
| Средний темп роста | 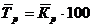 | |
| Средний темп прироста | 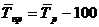 | Показывает, на сколько процентов произошло увеличение (снижение) показателя в среднем в единицу времени. |
где 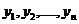 - уровни ряда динамики;
- уровни ряда динамики;
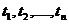 - интервалы времени между смежными датами;
- интервалы времени между смежными датами;
n – число уровней ряда;
m – число коэффициентов роста;
уn- последний уровень временного ряда;
у0 - базисный (начальный) уровень ряда.
При анализе рядов динамики необходимо определить общую тенденцию развития. На развитие явления во времени могут оказывать влияние различные факторы, одни из них могут формировать в рядах динамики определенную тенденцию в развитии, другие - оказывают кратковременное воздействие.
При выявлении общей тенденции развития явления применяются различные приемы и методы выравнивания:
а) усреднение по левой и правой половине;
б) укрупнение интервалов;
в) сглаживание рядов динамики на основе скользящих средних;
г) аналитическое выравнивание и др.
Рассмотрим два последних метода. Сглаживание рядов динамики на основе скользящих средних основана на вычислении звеньев подвижной средней из такого числа уровней ряда, которая соответствует длительности наблюдаемых в ряду динамики циклов. То есть изначально выбирается период скольжения, равный двум, трем, четырем и т.д. периодам.
Например, трехчленная скользящая средняя исчисляется по следующей схеме:
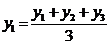 (первая средняя),
(первая средняя),
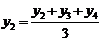 (вторая средняя),
(вторая средняя),
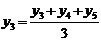 (третья средняя) и т.д.
(третья средняя) и т.д.
А для ряда внутригодовой динамики применяется чаще всего четырехчленные скользящие средние. Их расчет состоит в определении средних величин из четырех уровней ряда с отбрасыванием при вычислении каждой новой средней одного уровня ряда слева и присоединением одного уровня справа:
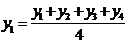 (первая средняя),
(первая средняя),
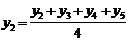 (вторая средняя),
(вторая средняя),
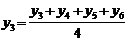 (третья средняя) и т.д.
(третья средняя) и т.д.
Чтобы отнести скользящую среднюю к определенному периоду необходимо провести центрирование расчетных средних, определяемых как простая средняя арифметическая из 2-х рядом лежащих скользящих средних:
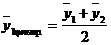 (1-й сглаженный средний уровень),
(1-й сглаженный средний уровень),
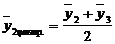 (2-й сглаженный средний уровень)
(2-й сглаженный средний уровень)
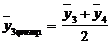 (3-й сглаженный средний уровень) и т.д.
(3-й сглаженный средний уровень) и т.д.
Пример
Таблица 8
