Перестановка членов сходящихся рядов.

Известно, что конечная сумма, обладая переместительным свойством, не меняется от перестановки местами слагаемых. Возникает вопрос: изме­нится ли сумма сходящегося ряда от перестановки членов ряда?

Пусть ряд(1) 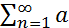_n сходится: 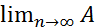_n=A. Объединим члены ряда произвольным образом в группы, не меняя при этом их порядка:

(2) 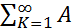_nk=(a₁+a₂+…+a_n)+(a_n1+1+…+a_n2)+…,где{n_i}–возрастающаяподпо­следовательность последовательности {n}.

Теорема (сочетательное свойство сходящегося ряда):Ряд (2) схо­дится и имеет ту же сумму, что и (1).

(Последовательность частичных сумм {A_n’} ряда (2)– подпоследо­вательность последовательности {A_n} ряда (1),а следовательно, сходится и имеет ту же сумму.)

Замечание.Обратное, вообще говоря, неверно. Но если все слагаемые внутри одних и тех же скобок в (2) одного знака, и ряд (2) – сходится, то скобки можно опустить, ряд (1) будет сходится.

Переместительное свойство абсолютно сходящегося ряда.

Теорема Дирихле-Коши:Если ряд (1) 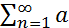_n –абсолютно сходится, тогда любой ряд вида (2), полученный из (1) произвольной перестановкой слагаемых также будет сходится абсолютно и иметь ту же cумму, что и ряд (1).

Теорема Римана:Если ряд (1) условно сходится, то 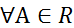в том числе для A=∞, можно так переставить члены ряда, что сумма его станет равна А. (без доказательства).

Вывод: абсолютно сходящиеся ряды обладают сочетательным и перемести­тельным свойствами, а условно сходящиеся – только сочетательным свой­ством.

Условная сходимость числового ряда осуществляется за счет взаим­ного погашения положительных и отрицательных слагаемых и зависит от порядка слагаемых. Абсолютная сходимость определяется только скоро­стью убывания общего члена и поэтому не зависит от порядка слагаемых.

10. Критерий Коши РСФП.

Теорема (Критерий Коши РСФП):Последовательность 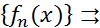f(x) :

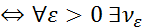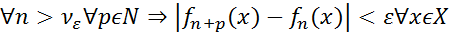
[Необходимость.Дано: f_n (x) 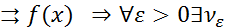: 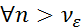, 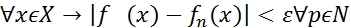n+p>n>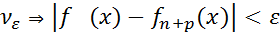

=

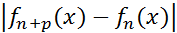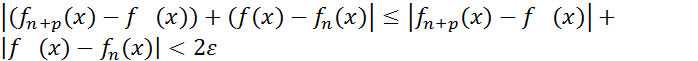
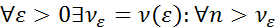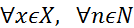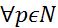
Достаточность. Дано: , , 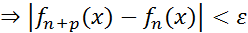(*). При 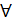фиксированном 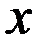числовая последова­тельность 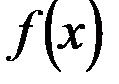–фундаментальна, а следовательно, сходится: = .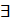

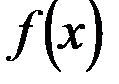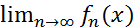В неравенстве (*) перейдем к пределу при p 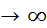: 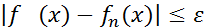, зна­чит,

.]

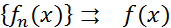11. Критерий Коши РСФР.

Теорема (Критерий Коши РСФР):Для того, чтобы ряд (2) : , , .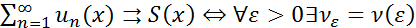

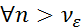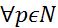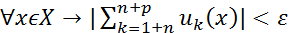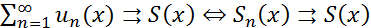[ - критерий Коши дока­зан. < .]

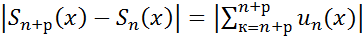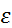Признаки Вейерштрасса и Дирихле

1) Теорема (достаточное условие равномерной сходимости функцио­нальных рядов (Вейерштрасса)):

Если членыфункционального ряда (2) 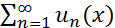удовлетворяют в обла­сти 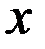неравенствам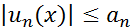 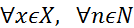, и 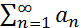сходящийся числовой ряд, 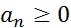. Тогда ФР (2) 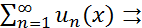, при этом числовой ряд 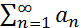называется мажорантой для ФР (2).

(Числовой ряд сходится, значит, по критерию Коши для числовых рядов 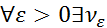: 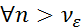, 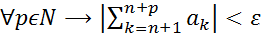Одновременно с этим
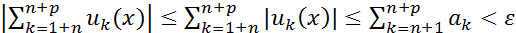, т.евыполняется крите­рий Коши равномерной сходимость для ФР.)

Пример:
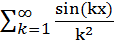, x 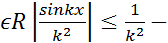так как мажорантный ряд сходится, то ФР сходится равномерно.

2) Теорема (признак Дирихле РСФР):(2 )

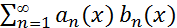
Если выполняются условия:

1)
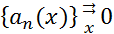
2) 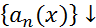– при каждом фиксированном х монотонно убывает

3) 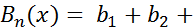...+ 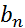, 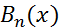– равномерно ограничена, т.е. 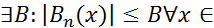X, тогда (2 )сходится равномерно.

Непрерывность суммы РСФР

Теорема (Непрерывность суммы равномерно сходящихся ФР):Пусть члены 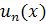ФР 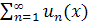непрерывны на [a,b], ряд равномерно сходится к S(x) на [a,b]. Тогда сумма ряда S(x) непрерывна на [a,b].

(Докажем 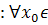[a,b] 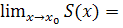S(x₀), т.е.

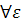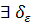>0 >0: .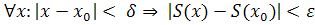

Рассмотрим (*).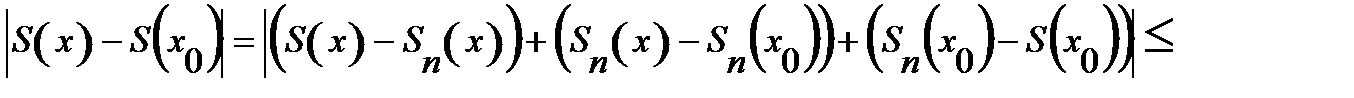

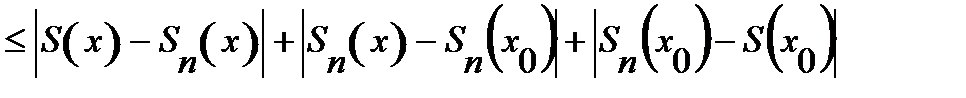Так как:

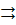
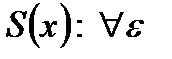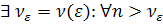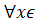а) ФР >0 , [a,b] 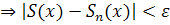(в том числе для );

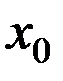в) 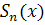=u₁(x)+...+u_n(x)- непрерывна на[a,b]

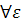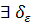>0 >0: 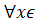[a,b]: 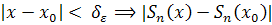< 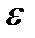, то в силу (*) при 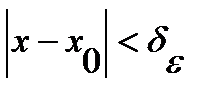выполняется . )

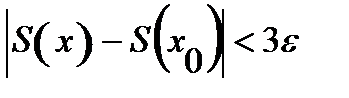Замечание. = =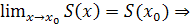

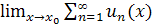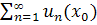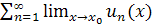
Замечание. Условия теоремы носят достаточный, но не обходимый харак­тер (т.е. есть ряды составленные из непрерывных функций сходятся нерав­номерно, но имеют непрерывную сумму)