Кручение бруса прямоугольного поперечного сечения

Данная задача является более сложной, чем предыдущая, т.к. здесь не справедлива гипотеза плоских сечений. Отдельные точки сечения перемещаются вдоль оси стержня, и все сечение в целом перестает быть плоским. Происходит так называемая депланация сечения (рис. 3.15).

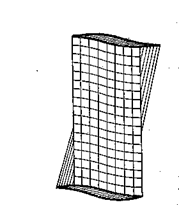
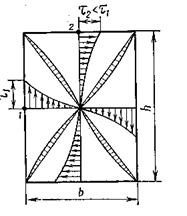
Рис. 3.15 Рис. 3.16

Точное решение данной задачи дается в курсе теории упругости. Здесь приведем только окончательные результаты для стержня прямоугольного сечения. На рис 3.16 приведены эпюры 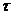для сечений по осям и диагоналям прямоугольного сечения.

Наибольшие касательные напряжения будут в середине длинной стороны прямоугольника.

; .

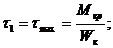
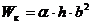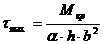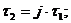причем .

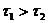Угол закручивания равен

; .

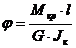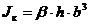Входящие в эти формулы коэффициенты 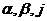зависят от отношения сторон 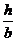и даны в таблице 1.

Таблица 1

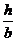		1.5	1.75		2.5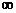
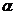	0.208	0.231	0.239	0.246	0.258	0.267	0.282	0.299	0.307	0.313	0.333
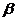	0.141	0.196	0.214	0.229	0.249	0.263	0.281	0.299	0.307	0.313	0.333
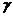	1.000	0.859	0.820	0.795	0.766	0.753	0.745	0.743	0.742	0.742	0.742

Потенциальная энергия бруса при кручении

Будем считать, что материал стержня работает при напряжениях, не превышающих предел упругости (рис. 3.17).

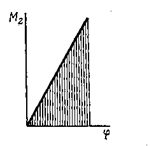
Рис. 3.17

В этом случае работа внешних сил, затрачиваемая на кручение стержня, равна потенциальной энергии, накопленной в стержне .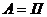

Работа равна площади треугольника

.

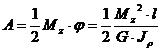Таким образом, потенциальная энергия бруса длиной 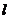скручиваемого по концам моментами равна

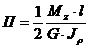. (3.15) Если изменения 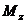и жесткости 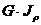происходит ступенчато, то потенциальная энергия подсчитывается для каждого участка.

Кручение бруса круглого поперечного сечения за пределом упругости

Для решения задачи примем диаграмму Прандтля (рис. 3.18).

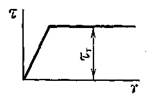
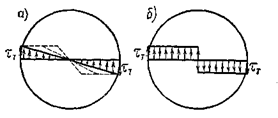
Рис. 3.18 Рис. 3.19

Когда касательные напряжения в точках контура достигнут предела текучести 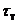, крутящий момент можно определить по обычной формуле

.

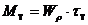Эпюра 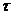для этого случая показана на рис. 3.19,а. При дальнейшем увеличении крутящего момента образуется кольцеобразная пластичная зона, постепенно проникающая внутрь сечения. Эпюра показана пунктиром. Таким образом, пластичная зона доходит до центра сечения. В последнем случае эпюра 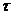имеет вид (рис. 3.19,б).

Предельный разрушающий момент равен

.

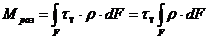Согласно рис. 3.20 имеем

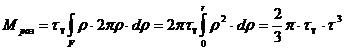
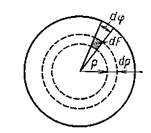
Рис. 3.20

Обозначим 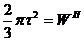пластический момент сопротивления при

кручении.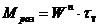

Сравнив выражение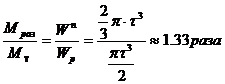

Если предположить, что коэффициент запаса прочности для двух рассмотренных случаев одинаков, то момент, найденный по разрушающей нагрузке будет на 33% выше момента, найденного по допускаемым напряжениям.

Глава 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

Основные понятия

При растяжении (сжатии) мы встречались с простейшей геометрической характеристикой поперечного сечения — площадью 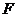. При изгибе и кручении этой характеристики недостаточно.

Возьмем, к примеру, брус прямоугольного поперечного сечения с площадью 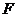, приложим к свободному концу силу 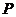(рис. 4.1)

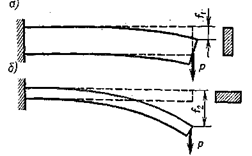
Рис. 4.1

Расположим его сечение по отношению к нагрузке как показано на рис. 4.1,а,б. В зависимости от ориентации сечения прогибы 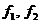будут разными.

Вывод: площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу. Необходимо привлекать к рассмотрению более сложные геометрические характеристики.

Статические моменты сечения

Возьмем некоторое поперечное сечение бруса (рис. 4.2)

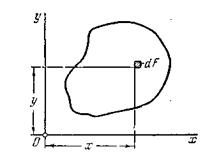
Рис. 4.2

Свяжем его с системой координат 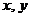и рассмотрим два следующих интеграла

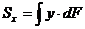
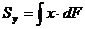(4.1)

Индекс 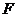у интеграла означает, что интегрирование ведется по всей площади сечения.

Первый интеграл называется статическим моментом сечения относительно оси 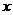, а второй статическим моментом относительно оси 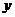. Размерность — .

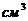При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осе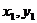й и 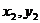(рис. 4.3).

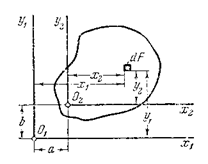
Рис. 4.3

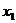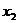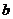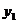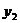Пусть расстояние между осями и равно , а между и равно 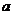. Дано: 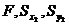. Требуется определить .

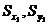Очевидно, что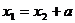

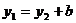
Искомые статические моменты равны

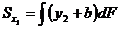
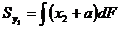
Или .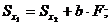

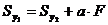Рассмотрим подробнее, например, первое из полученных выражений

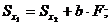
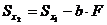
Величина 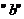может быть как положительной, так и отрицательной. Всегда можно подобрать 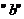так, причем единственным образом, чтобы,

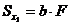, тогда 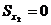. Ось, относительно которой статический момент равен “0”, называется центральной.

Расстояние до центральной оси от некоторой произвольной 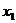равно

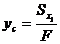, (4.2)

аналогично

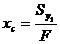. (4.3)

Таким образом, с помощью формул (4.2), (4.3) можно найти центр тяжести любой фигуры.