Статистические гипотезы. Нулевая и конкурирующая гипотезы. Ошибки 1-го и 2-го рода. Стат. критерий проверки нулевой гипотезы.

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений. Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Нулевой (основной) называют выдвинутую гипотезу Н₀.Конкурирующей (альтернативной) называют гипотезу Н₁, которая противоречит нулевой.

Выдвинутая гипотеза может быть правильной и неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки 2-х родов. Ошибка 1-го рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку 1-го рода называется уровнем значимости и обозначается α. На практике обычно равна 0,05 или 0,01.

Стат. критерий – СВ-на К, которая служит для проверки нулевой гипотезы.

Наблюдаемым значением называют значение стат. критерия, вычисленное по данным выборки. Критической областью называют совокупность значений критерия К, при которых нулевую гипотезу отвергают. Областью принятия гипотезы называют совокупность значений критерия К, при которых гипотезу принимают. Критическими точками называют точки, отделяющие критическую область от области принятия гипотезы. Критические области бывают правосторонние и левосторонние.

Принцип проверки стат. гипотезы: если К_набл принадлежит критич. области, то нулевую гипотезу отвергают; если К_набл принадлежит области принятия гипотезы, то нет оснований отвергать нулевую гипотезу. Для каждого критерия имеются спец. таблицы, по которым находятся критич. точки для заданного уровня значимости α.

3.19.Критической областью наз.сов-ть знач.критерия,при кот-х нулевую гипотезу отвергают.Областью принятия гипотезыназ.сов-ть знач.критерия,при кот-х гипотезу принимают.Критическими точками наз.точки,отделяющие критическую область от области принятия гипотезы.Различают одностороннюю и двустор.критич.области.Правостор.наз.критич.область,определяемую нерав-ом К›к_кр,где к_кр-полож.число.Левостор.наз.критич.область,опред-ую нер-ом К‹к_кр,где к_кр-отриц.число.Одностор.наз.правостор.или левостор.критич.область.Двустороннейназ.критич.область опред.нер-ми К‹к₁,К›к₂,где к₂›к₁.Для отыскания правостор.критич.области достаточно найти критич.точку.Для её нахождения задаются достаточной малой вероятностью-уровнем значимости α.Затем ищут критич.точку,исходя из требования,чтобы при усл.справедливости нулевой гипотезы вероятность того,что критерий примет значение,большее к_кр,была равна: Р(К›к_кр)=α.Левостор.критич.область опр-ся нер-ом К‹к_кр(к_кр‹0).Критич.точкунаходят исходя из требования,чтобы при справедливости нулевой гипотезы вероятность того,что критерий примет знач.,меньшее к_кр,была равна Р(К‹к_кр)=α. Двустор.критич.обл.опр.нер-ми К‹к₁,К‹к₂.Критич.точки нах-т из трбования,чтобы при справедл-ти нулевой гипотезы сумма вер-тей того,что критерий примет знач.,меньшее к₁ или большее к_2, была равна: Р(К‹к₁)+Р(К›к₂)=α.Мощностьюназ.вер-ть попадания критерия в критич.обл.при усл.,что справедлива конкурирующая гипотеза.

3.23Если хi (i=1,2,…,n)результаты измерений деталей первым прибором, а уi – результаты измерений этих же деталей, произведённые этим же деталей вторым прибором, то хi и уi попарно зависимы, и в этом смысле сами выборки зависимые. Поскольку, как правило хi≠уi, возникает необходимость установить, значимо или незначимо различаются пары этих чисел. Если подтверждается нулевая гипотеза, то пишем: 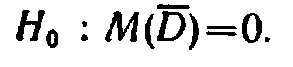, тогда конкурирующая гипотеза имеет вид: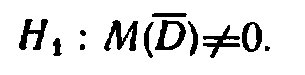

3.24Для сравнения сущ-т след-ее правила:

1. для того, чтобы при заданном уровне значимости проверить нулевую гипотезу Н0 : а=а0, при конкурирующей гипотезе Н1:а≠а0, надо вычислить наблюдаемое значение критерия: 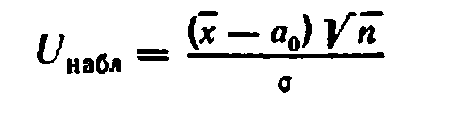и по таблице функции Лапласа найти критическую точку двусторонней критической области по равенству 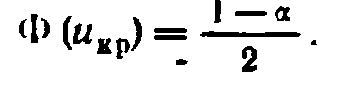. Если │Uнабл│< Uкр – нет оснований отвергнуть нулевую гипотезу, если │Uнабл│> Uкр – нулевую гипотезу отвергают.

2.При конкур-й гипотезе Н1: а>а 0, критическую точку находят: 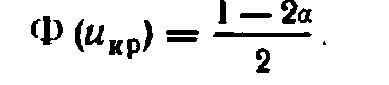. Если Uнабл<Uкр- нет осн-й отвергать нулевую гипотезу, если Uнабл>Uкр – нулевую гип отвергают.

3. При конкур гипотезе Н1:а<а 0 сначала находят критическую точку по правилу 2, а затем границу левосторон-й критической области 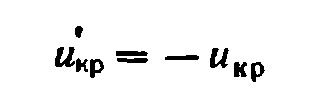. Если Uнабл>-Uкр – нет оснований отвергать 0 гип-зу, если Uнабл<-Uкр – нулев гипотезу отвергают.

3.25На практике часто известна величина (точность) ϭ>0, которую не должна превышать абсолютная величинаразности междувыборочной и гипотетической генеральной средними. Н-р: часто требуют, чтобы средний размер изготовляемых деталей отличался от проектного не более, чем на заданное значение. 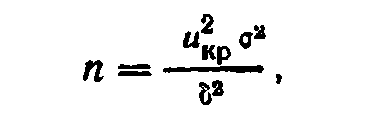- формула минимального объёма выборки.

3.26 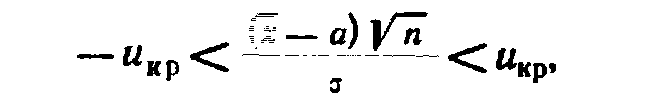или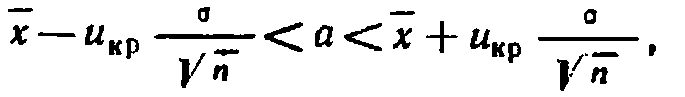 -неравенство, определяющее связь.

Мощность критерия- это вер-ть того, нулевая гипотеза будет отвергнута, если справедлива конкурирующая гипотеза