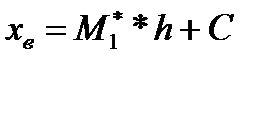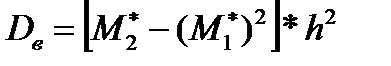Метод наибольшего правдоподобия дя дискретных и непрерывных СВ.

Метод наибольшего правдоподобия точечной оценки неизвестных параметров
заданного распределения сводится к отысканию максимума функции одного или
нескольких оцениваемых параметров. Д.С.В. Пусть Х – Д.С.В., которая в
результате n опытов приняла возможные значения х1,х2,…,xn. Допустим, что
вид закона распределения величины Х задан, но неизвестен параметр (,
которым определяется этот закон; требуется найти его точечную оценку (*=(
(x1,x2,…,xn). Обозначим вероятность того, что в результате испытания
величина Х примет значение xi через р(xi;(). Функцией правдоподобия Д.С.В.
Х называют функцию аргумента (: L (x1,x2,…,xn;()=p(x1;()*p(x2;()…p(xn;().
Оценкой наибольшего правдоподобия параметра ( называют такое его значение
(*, при котором функция правдоподобия достигает максимума. Функции L и lnL
достигают максимума при одном и том же значении (, поэтому вместо отыскания
максимума функции L ищут, что удобнее, максимум функции lnL. Н.С.В. Пусть Х
– Н.С.В., которая в результате n испытаний приняла значения х1,х2,…,xn.
Допустим, что вид плотности распределения – функции f(x) – задан, но
неизвестен параметр (, которым определяется эта функция. Функцией
правдоподобия Н.С.В. Х называют функцию аргумента (:
L(x1,x2,…,xn;()=f(x1;()*f(x2;()…f(xn;().

3.14. Условные варианты. Обычные, начальные и центр. Эмперич. Моменты. Условные эмпирич. Моменты. Метод произведений для вычисления выборочн. Средней и выбороч. Дисперсии.

Условными наз. Варианты, определ-ые рав-вом 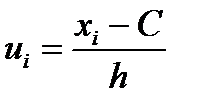, где С- ложный нуль(новое начало отсчета), h- шаг, т. е. разность м/у любыми двумя соседними первонач. Вариантами( новая ед. масштаба).

Обычным эмпирич. Моментом порядка к наз. Средн. Знач-е к-степеней разности :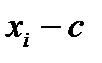

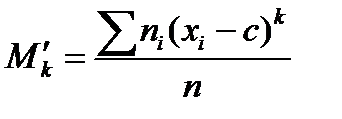, где

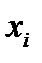- наблюд-ая варианта,

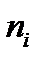- частота варианты,

n = 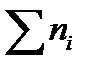- объем выборки,

с –произвольн. Постоян. Число

Начальным эмпирич. Моментов порядка к наз. Обычный момент порядка к при с = 0:

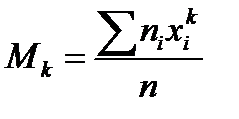
Центр. эмпирич. Моментом порядка к наз. Обычный момент порядка к при с = :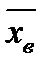

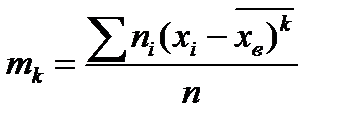
Условным эмпирич. Моментом порядка к наз. Начальный момент порядка к , вычеслен. Для условных вариант:

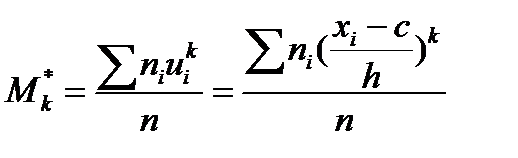
Метод произведенийдлявычисления выборочн. Средней и выбороч. Дисперсии: при использовании метода пользуются расчетной табл., кот. составляется так :

в 1 столбец записывают выбор.(первонач.) варианты по возрастанию

во 2 столбец записывают частоты вариант; складывают все частоты и их сумму помещают в нижнею клетку столбца

в 3 столбец записывают условные варианты 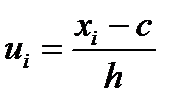, причем в кач-ве ложного нуля с выбирают варианту с наиб. Частотой и полагают h равным разности м/у любыми двумя соседними вариантами

умножают частоты на условные варианты и записывают их произ-ие 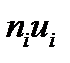в 4 столбец, сложив все получен. Числа, их сумму помещают в нижнюю клетку столбца

умножают частоты на квадраты условн. Вариант и записывают их произв-я 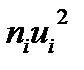в 5 солбец, сложив все получен. Числа, их сумму помещают в нижнюю клетку столбца

умножают частоты на квадраты условн. Вариант, увеличен. Каждая на ед-цу, и записывают произв-я 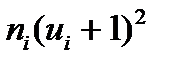в 6 контрольн. Столбец, сложив все получен. Числа, их сумму помещают в нижнюю клетку столбца

После того, как расчетн. Табл. Заполнена и проверена правильность вычислений, вычисляют условн. Моменты:

,

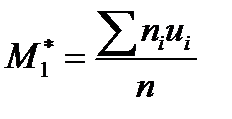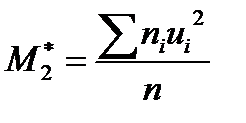
Наконец, вычисляют выборочн. Средн. И дисперсию: