Угловая скорость сферического движения твердого тела – вектор

направленный вдоль мгновенной оси вращения, модуль которого равен:

Угловое ускорение сферического движения твердого тела – характеризует изменение вектора угловой скорости:

- среднее угловое ускорение

в интервале времени Dt,

Угловое ускорение в момент времени t:

Вектор угловой скорости с началом в неподвижной точке при движении тела изменяется

подобно радиусу-вектору точки, движущейся в пространстве по некоторой траектории.

Вектор скорости этой точки направлен по касательной к траектории и определяется выражением:

Траектория конца вектора угловой скорости с началом в неподвижной точке при движении тела описывает кривую, называемую годографом вектора угловой скорости.

Сравнивая выражения для вектора углового ускорения тела и вектора скорости точки можно установить, что угловое ускорение тела геометрически равно линейной скорости конца вектора угловой скорости.

Прямая, по которой направлен вектор углового ускорения, называется осью мгновенного углового ускорения (E

Сферическое движение тела

Сферическим движением (движением тела с одной закрепленной точкой) называется такое движение тела, при котором одна его точка О остается неподвижной во все время движения. Все остальные точки тела движутся при этом по траекториям, расположенным на поверхности сфер с центром в неподвижной точке О. Положение тела определяется углами Эйлера (рис. 1): углом прецессии φ, углом нутации θ и углом собственного вращения φ. Эти углы характеризуют положение координатного трехгранника осей Oξηζ, связанного с телом, по отношению к неподвижному трехграннику Oxyz. Линия ON пересечения координатных плоскостей Оху и Oξη называется линией узлов.

Рисунок 1.

Уравнения сферического движения:

РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ. Во всякий момент времени существует проходящая через неподвижную точку О прямая OΩ, скорости точек которой равны нулю. Это мгновенная ось вращения. Мгновенная угловая скорость 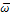определяется соотношением

где - векторы, численно равные производным углов Эйлера и направленные соответственно по осям z, ON и ζ. Мгновенная угловая скорость может менять свое положение в пространстве, описывая коническую поверхность, поэтому вектор углового ускорения

в общем случае не совпадает по направлению с 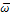(рис. 2).

Рисунок 2.

Скорость точки при сферическом движении тела

или в аналитической форме (формулы Эйлера):

Ускорение точки складывается из осестремительной 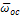и вращательной 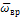составляющих (рис. 2):

Формулы Пуассона.

При рассмотрении вращательного движения тела вокруг неподвижной оси получена векторная формула Эйлера, по которой скорости точек тела полностью характеризуются общей для всех точек тела угловой скоростью вращения и расположением точек тела относительно оси вращения.

Cкорость v какой-либо точки М тела , по векторной формуле Эйлера:

υ= ω* r

Скорость какой-либо точки можно вычислить как первую производную по времени от радиуса-вектора г этой точки, проведенного из неподвижной точки. С другой стороны, скорость точки тела, вращающегося вокруг неподвижной точки, можно вычислить по векторной формуле Эйлера. Следовательно, производная по времени от радиуса-вектора любой точки твердого тела, вращающегося вокруг неподвижной точки, определится по формуле

dr/dt=ω*r

Длина радиуса-вектора г как расстояние между двумя точками твердого тела является постоянной величиной при движении этого тела. Следовательно, равенство dr/dt=ω*r можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого постоянен, и изменение этого вектора происходит только вследствие вращения его с угловой скоростью ш вместе с телом вокруг неподвижной точки.

Если взять подвижную систему координат Oxyz, скрепленную с телом, которое вращается вокруг неподвижной точки с угловой скоростью ω, то для единичных векторов i, j, k направленных по этим осям координат, как для векторов, модули которых постоянны имеем:

di//dt = ω*i ; dj/dt = ω *j; dk/dt = ω*k

Эти формулы называют формулами Пуассона.