Наибольшее возможное число корней в области целостности.

Т1: Число корней не нулевого многочлена не превосходит его степени.

Доказательство:

Докажем теорему индукцией по степени многочлена:

Если многочлен f(x)=a где a=const, 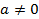. Если f(x)=s то f(x) не имеет корней.

Пусть ст f(x) ≥1. Предположим, что утверждение теоремы верно для всех многочленов степени n-1. Докажем истинность утверждения для любого мочалена степени n, с помою метода от противного. Путь многочлен имеет корни 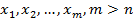. По теореме Безу имеем:

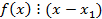то есть выполняется равенство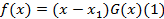

cт g(x)=n-1

Покажем, что оставшиеся корни 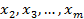должны быть корнями многочлена g(x)

Положим что, 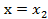в равенстве (1):

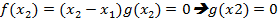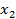è корень g(x). Аналогичные равенства выполняются для 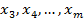, 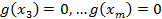èмногочлен g(x) имеет m-1 корней èст g(x)=m-1 но по предположению ст g(x) =n-1 оп этому наше предположение оказалось не верным а, следовательно теорема доказана.

Следствие: многочлен степени не выше n однозначно определяется своими значениями в n+1 точках то есть существует не большие одного многочлена степени не выше n принимающего в n+1 точках 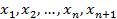, n+1 различных значений .

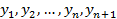Докажем:

Пусть f(x) и g(x) степени не выше n, принимающее одинаковые значения в точках 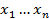рассмотрим h(x)=f(x)-g(x) степень которого также не выше n. Так как 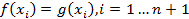то 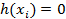тоесть 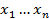корни многочлена h(x) тогда по Т1 сам многочлен h(x)=0èf(x)=g(x).

Т2: Если кольцо K бесконечно, то равенство функций определяемых многочленами с коэффициентами из кольца K влечет за собой равенство самих многочленов.

Доказательство:

Пусть разные функции f(x) g(x) с коэффициентами из поля K. Пусть n максимальная из степеней данных многочленов n=max(ст(f(x),ст(g(x)). Выберем 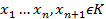по условию функций определяемые многочленами равны между собой. 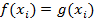и на основании следствия к Т1 мы можем утверждать что, f(x)=g(x) для любого x из K.

Замечание: понятие функционального равенства многочленов отличается от алгебраического равенства функциональное равенство означает что, многочлены принимают одинаковы значения в одних и тех же точках при чем разные многочлены могут определять одну и туже функцию.

Деление с остатком

Между кольцом многочленов от одной переменной и кольцом целых чисел имеется глубокая аналогия проявляющаяся в свойствах делимости, в разложении на простые множества причина аналоги состоит в том что, в обоих этих кольца выполнимо деление с остатком благодаря чему оба эти кольца являются евклидовыми.

Т(Делении с остатком): Пусть P произвольное поле, P[x] кольцо многочленов с коэффициентами из P возьмем f(x) и g(x)≠0 тогда существует единственная пара многочлена q(x),r(x) ∈P[x] удовлетворяющая условиям:

1)f(x)=g(x)q(x)+z(x)

2)ст z(x)<ст g(x).

Доказательство:

Пусть:

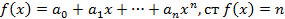
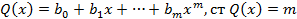
Если n<m то не полное частное равно 0 а, остаток совпадет с самим многочленом f(x).

Рассмотри когда n≥m. Построим многочлен ,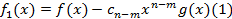

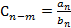
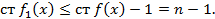Обозначим .

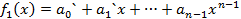Аналогично построим 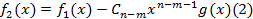. Где , .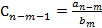

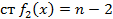Продолжая процесс построения многочленов будет получена конечная последовательность многочленов и последний многочлен будет иметь номер n-m+1 и имеет степень 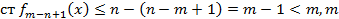-степень многочлена g(x). Последний многочлен: 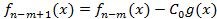. Почвенное сложение равенств (1) (2) и т.д. дает возможность выразить многочлен f(x) через g(x):

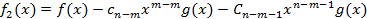
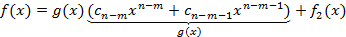
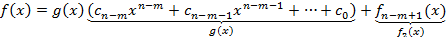
То есть наш многочлен представим в виде:

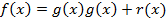
Докажем единственность такова представления методом от противного.

Предположим что, существуют такие многочлены 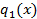и 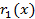что, выполняется: 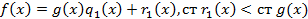тогда:

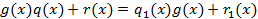
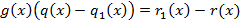
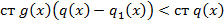
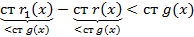
Учитывая что, степень левой части больше или равна а, степень правой ее не превосходит получили противоречие из которого следует: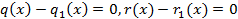

Рассмотренная процедура деления с остатком лежит в основе отыскания наибольшего делителя 2 многочленов.