Условная вероятность. Независимые события. Теорема умножения вероятностей. Вероятность произведения конечного числа событий.

1) Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А|В) или PB(A).

Условная вероятность события А при условии наступления события В равна

Р(А|В)= Р(АB) /P(B) ,

Эта формула называется формулой условной вероятности.

Условие независимости события А от события В можно записать в виде:

Р(А|В)= Р(А)

2) События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

3) Теорема

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

P(AB) = P(A)P(B|A).

Доказательство:

Пусть возможные исходы опыта сводятся кn элементарным событиям.

Предположим, что событию A благоприятны m элементарных событий, а событию Bблагоприятны k элементарных событий. Так как мы не предполагали события А и В несовместными, то вообще существуют элементарные события, благоприятные и событию А, и событию В одновременно. Пусть число таких элементарных событий l. Тогда

P(AB) = l / n ,, P(A) = m / n

Вычислим P(B|A), т.е. условную вероятность события В в предположении, что А имело место. Если известно, что событие А произошло, то из ранее возможныхn элементарных событий остаются возможными только m, которые благоприятствовали событию А. Из них l элементарных событий благоприятны событию В. Следовательно,

P(B|A) = l / m.

Подставим полученные выражения в P(AB)=P(A)P(B|A)

l /n =( m / n) ґ (l / m).

Получили тождество. Теорема доказана.

Рассмотрим следствия, вытекающие из теоремы умножения.

Следствие 1

Если событие А не зависит от события В, то и событие В не зависит от события А.

Доказательство:

Дано, что событие А не зависит от события В, т.е.

P(A) = P(A|B),

Требуется доказать, что и событие В не зависит от А, т.е.

P(B) = P(B|A),

При доказательстве будем предполагать, что P(A)№ 0.

Напишем теорему вероятностей в двух формах:

P(AB)=P(B)P(A|B),

P(AB)=P(A)P(B|A).

Откуда

P (A)P(B|A)=P(B)P(A|B)

Или так как событие А не зависит от В, т.е. P(A) = P(A|B), то

P(A)P(B|A)=P(B)P(A).

Разделим обе части равенства на P(A). Получим:

P(B|A)=P(B).

Что и требовалось доказать.

Итак, два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Следствие2.

Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

При вычислении условной вероятности сужается пространство элементарных событий. Поясним это. Пусть задана некоторая полная группа событий w1, w2,w3,…,w n , несовместных и равновероятных между собой, и на основании ее установлены вероятности событий в множестве допустимых событий А,В и т.д. При вычислении условной вероятности решается вопрос, как должны измениться вероятности, если предположить, что станет достоверным наступление одного из допустимых событий, например А. Предположение, что стало достоверным событие А, нарушает заданную полную группу несовместных между событий w1, w2,w3,…,wn в том смысле, что благодаря этому предположению все события заданной группы уже не могут больше считаться равновероятными. А именно, предположение, что стало достоверным событие А, означает, что из всех событий w1, w2,w3,…,wn остаются возможными только те, на которые подразделяется А, остальные же становятся невозожными. z

4)Метод математической индукции позволяет обобщить эту формулу на случай n событий.

P(A₁A₂ x……x A_n)= P(A₁)P(A₂|A₁)x…x P(A_n|A₁A₂x…xA_n-1)

Вопрос 6

Формула полной вероятности. Формула Байеса.

Формула полной вероятности

Пусть дана группа несовместных событий В1,В2…Вn и некоторое событие А, подразделяющееся на частные случаи АВ1, АВ2… АВn. И пусть даны вероятности P(В1), P(В2),…,P(Вn) и условные вероятности P(A|В1), P(A|В2),…,P(A|Bn). Требуется определить вероятность P(A).

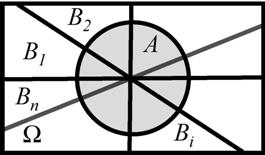
Рис. 2. Пояснение к формуле полной вероятности

Так как

A = АВ1 +АВ2 +…+ АВn,

То

P(A)= P(АВ1 + АВ2 +… +АВn ).

События В1, В2,…,Вn несовместные, следовательно, события АВ1,АВ2,…,АВn тоже несовместные. Воспользуемся теоремой сложения для несовместных событий.

P(A) = P(АВ1 + АВ2 +… +АВn) = P(АВ1)+ P(АВ2)+… +P(АВn )

По теореме умножения для каждого слагаемого имеем

P(ABi)=P(Bi)P(A|Bi).

Следовательно

P(A) = P(B1)P(A|B1) +P(B2)P(A|B2)+…+P(Bn)P(A|Bn).

Или

P(A) = 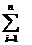P(B_i)P(A|B_i)