Понятие случайного события, элементарный исход, множество элементарных событий. Алгебра событий: сумма, произведение событий. Несовместные события. Полная группа событий. Противоположеные события.

Случайным называется событие, которое может произойти или не произойти в результате некото­рого испытания.

Испытание(опыт, эксперимент) — это процесс, включающий определенные условия и приводящий к одному из нескольких возможных исходов. Исхо­дом опыта может быть результат наблюдения или измерения

Единичный, отдельный исход испытания назы­ваетсяэлементарным событием.

Случайное событие может состоять из несколь­ких элементарных событий, подразделяющихся на достоверные, невозможные, совместные, несовместные, единственно возможные, равновозможные, противоположные.

Событие, которое обязательно произойдет в ре­зультате испытания, называетсядостоверным.

На­пример, если в урне содержатся только белые шары, то извлечение из нее белого шара есть событие дос­товерное; другой пример, если мы подбросим вверх камень, то он обязательно упадет на землю в силу действия закона притяжения, т. е. результат этого опыта заведомо известен. Достоверные события ус­ловимся обозначать символом

Событие, которое не может произойти в резуль­тате данного опыта (испытания), называетсяне­возможным.

Извлечение черного шара из урны с белыми шарами есть событие невозможное; выпадение выигрыша на все номера облигаций в каком-либо тираже выигрышного займа также невозможное событие.

Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элемен­тарных исходов.

Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их со­вместного наступления

Р(А + В) = Р(А) + Р(В) - Р(АВ),

или (2.4)

Р(А È В) - Р(А) + Р(В) - Р(А Ç В).

Для несовместных событий их совместное на­ступление есть невозможное событие, а вероятность его равна нулю, следовательно, вероятность сум­мы двух несовместных событий равна сумме вероятностей этих событий.

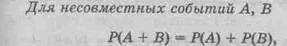
или (2.5)

Р(А È В) = Р(А) + Р(В).

Правило сложения вероятностей справедливо и для конечного числа п попарно несовместных событий

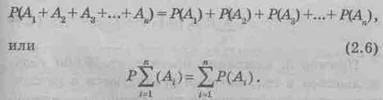
В случае нескольких совместных событий необ­ходимо по аналогии с рассуждениями о пересечении двух совместных событий исключить повтор­ный учет областей пересечения событий. Рассмот­рим три совместных события (рис.2.3).

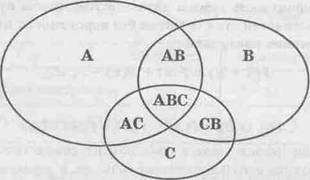
Рис.2.3

Для случая трех совместных событий можно записать

Р(А + В + С) = Р(А) + Р(В) + Р(С) - Р(АВ)- Р(АС) - Р(ВС) + Р(АВС).

Сумма вероятностей событий А₁, А₂, А₃ , ..., А_n, образующих полную группу, равна 1

Р(А₁) + Р(А₂) + Р(А₃) + ... + Р(А_n) = 1.

или

Вероятность произведения двух независимых со­бытий А и В равна произведению их вероятностей

Р(А В) = Р(А)Р(В),

или (2.8)

Р(А Ç В) = Р(А)Р(В).

События А₁, А₂, ..., А_n(п > 2) называются неза­висимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.

Распространим теоремы умножения на случаи п независимых и зависимых в совокупности событий.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна про­изведению вероятностей этих событий

Р(А₁·А₂·А₃·...·А_n) = Р(А₁)·Р(А₂)·Р(А₃)·...·Р(А_n). (2.9)

Вероятность произведения двух зависимых со­бытий А и В равна произведению вероятности од­ного из них на условную вероятность другого

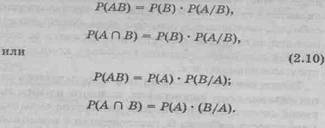
Несколько событий называются несовместны­ми в данном опыте, если появление одного из них исключает появление других.

Например, выигрыш, ничейный исход и проигрыш при игре в шахматы (одной партии) — 3 несовместных события

Несколько событий называются совместными, если в результате эксперимента наступление од­ного из них не исключает появления других.

Например, при бросании 3 монет выпадение цифры на одной не исключает появления цифр на других монетах.

Совокупность всех единственно возможных и не­совместных событий называется полной группой событий.

Различные события и действия с ними удобно рассматривать с помощью так называемых диаграмм Венна (по имени английского математика-логика Джона Венна).

Изобразим полную группу событий в виде квад­рата, тогда круг внутри квадрата будет обозначать некоторое событие, скажем. А, а точка - элемен­тарное событие - Е (рис. 2.1).

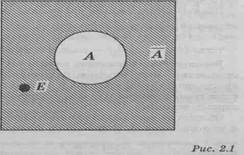
Рис. 2.1 демонстрирует два противоположных со­бытия А и не А, которые дополняют друг друга до полной группы событий. Противоположное событие обозначается Ā.

Два единственно возможных и несовместных со­бытия называются противоположными.

Купля и продажа определенного вида товара есть события противоположные.