Формула полной вероятности. Формула Байеса.

Самаров- ТЕОРИЯ ВЕРОЯТНОСТЕЙ.pdf - стр. 5

+

Формула полной вероятности.Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,

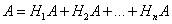
Применяя аксиому сложения вероятностей, имеем

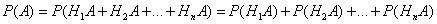
Но 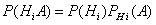(i=1, 2, ..., n), поэтому

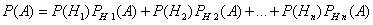
Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».

Формула Байеса. Предположим, что производится некоторый опыт, причем об условиях его проведения можно высказать n единственно возможных и несовместных гипотез 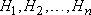, имеющих вероятности 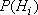. Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы 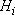, то , .

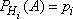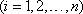Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей .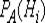

Имеем ,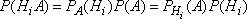

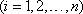
Откуда

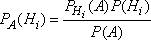
Но по формуле полной вероятности

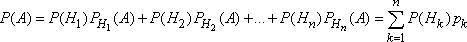
Поэтому

,

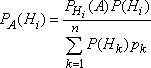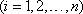
Формула называется формулой Бейеса.

Последовательность независимых испытаний Бернулли. Формула Бернулли для числа «успехов».

Самаров- ТЕОРИЯ ВЕРОЯТНОСТЕЙ.pdf - стр. 6

+

Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А равна P(A)=p и, следовательно, вероятность противоположного события (ненаступления А) равна 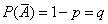. Определим вероятность P_n(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и 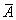. Например, запись 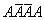означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.

Всякую комбинацию, в которую А входит m раз и 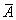входит n-m раз, назовем благоприятной. Количество благоприятных комбинаций равно количеству k способов, которыми можно выбрать m чисел из данных n; таким образом, оно равно числу сочетаний из n элементов по m, т.е.

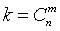
Подсчитаем вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых m испытаниях и, следовательно, не происходит в остальных n-m испытаниях. Такая благоприятная комбинация имеет следующий вид:

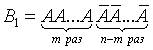
Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет

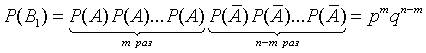
Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей)

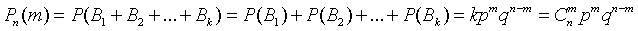
Следовательно,

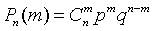
или, так как 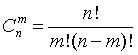, то

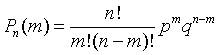- формулой Бернулли.