Основные свойства определителей

• Величина определителя не изменится, если все его строки заменить на столбцы с теми же номерами, т. е.

= .

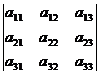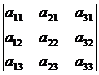• При перестановке двух строк (столбцов) определитель меняет свой знак; например,

= - .

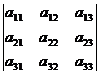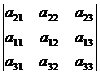• Общий множитель всех элементов какой-либо строки (столбца) определителя можно вынести за знак определителя; например

= .

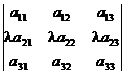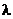
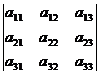• Если некоторые строки (столбцы) определителя целиком состоят из нулей, то определитель равен нулю.
• Если элементы какой-либо строки (столбца) определителя пропорциональны (в частности, равны) соответствующим элементам другой строки (столбца), то определитель равен нулю; например,

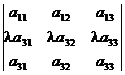= 0.

• Если каждый элемент какой-либо i-й строки (столбца) определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей, отличающихся от данного определителя только i-й строкой (столбцом); i-я строка (столбец) одного из этих определителей состоит из первых слагаемых, другого определителя – из вторых слагаемых; например

= + .

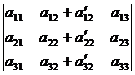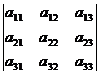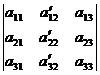• Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на любой общий множитель; например

= .

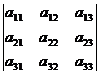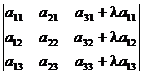• Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
• Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю; например

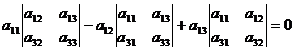
(здесь взяты элементы первой строки и алгебраические дополнения элементов

второй строки).

IV. ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ№1.Элементы линейной алгебры. «Матрицы и определители».

N Вариантa	Контрольная работа №1
	1.1, 2.1, 3.1, 4.1, 5.1, 6.1
	1.2, 2.2, 3.2, 4.2, 5.2, 6.2
	1.3, 2.3, 3.3, 4.3, 5.3, 6.3
	1.4, 2.4, 3.4, 4.4, 5.4, 6.4
	1.5, 2.5, 3.5, 4.5, 5.5, 6.5
	1.6, 2.6, 3.6, 4.6, 5.6, 6.6
	1.7, 2.7, 3.7, 4.7, 5.7, 6.7
	1.8, 2.8, 3.8, 4.8, 5.8, 6.8
	1.9, 2.9, 3.9, 4.9, 5.9, 6.9
	1.10, 2.10, 3.10, 4.10, 5.10, 6.10
	1.11, 2.11, 3.11, 4.11, 5.11, 6.11
	1.12, 2.12, 3.12, 4.12, 5.12, 6.12
	1.13, 2.13, 3.13, 4.13, 5.13, 6.13
	1.14, 2.14, 3.14, 4.14, 5.14, 6.14
	1.15, 2.15, 3.15, 4.15, 5.15, 6.15
	1.16, 2.16, 3.16, 4.16, 5.16, 6.16
	1.17, 2.17, 3.17, 4.17, 5.17, 6.17
	1.18, 2.18, 3.18, 4.18, 5.18, 6.18
	1.19, 2.19, 3.19, 4.19, 5.19, 6.19
	1.20, 2.20, 3.20, 4.20, 5.20, 6.20
	1.21, 2.21, 3.21, 4.21, 5.21, 6.21
	1.22, 2.22, 3.22, 4.22, 5.22, 6.22
	1.23, 2.23, 3.23, 4.23, 5.23, 6.23
	1.24, 2.24, 3.24, 4.24, 5.24, 6.24
	1.25, 2.25, 3.25, 4.25, 5.25, 6.25

V. ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ № 1 по вариантам c образцами выполнения 0-го варианта по разделу «Элементы линейной алгебры» по теме «Матрицы и определители».

1. ВЫЧИСЛИТЬ ОПРЕДЕЛИТЕЛИ:

N варианта	Определитель 2-го порядка	Определитель 3-го порядка	Определитель 4-го порядка
1.1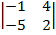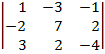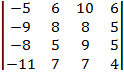
1.2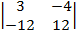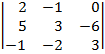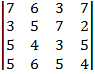
1.3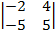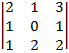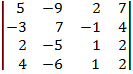
1.4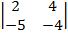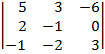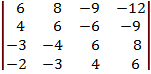
1.5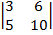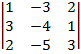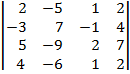
1.6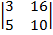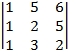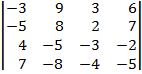
1.7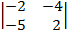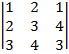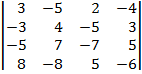
1.8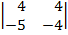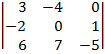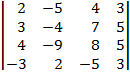
1.9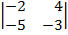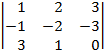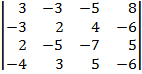
1.10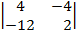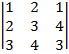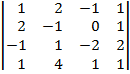
1.11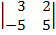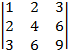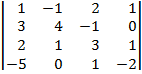
1.12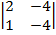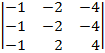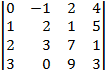
1.13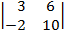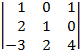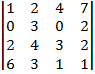
1.14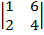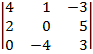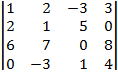
1.15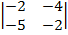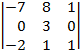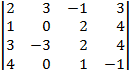
1.16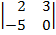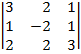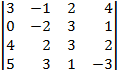
1.17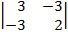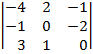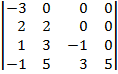
1.18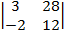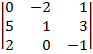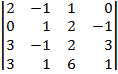
1.19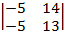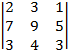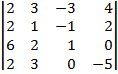
1.20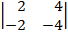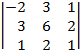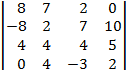
1.21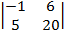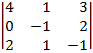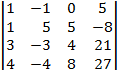
1.22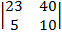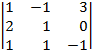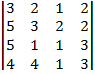
1.23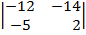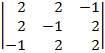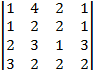
1.24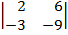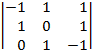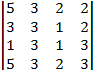
1.25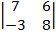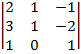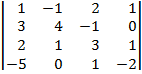

ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 1-го задания:

1. Вычислить определители:

N варианта	Определитель 2-го порядка	Определитель 3-го порядка	Определитель 4-го порядка
0.1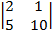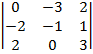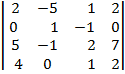

1. Определителем 2-го порядка называется число 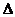, которое определяется равенством: . .

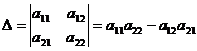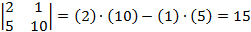2. Определителем 3-го порядка называется число 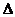, которое определяется, в частности, равенством:

,

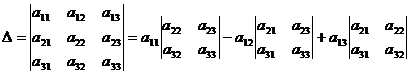(разложение определителя третьего порядка по элементам первой строки). Аналогично определитель 3-го порядка можно разложить по элементам других строк или столбцов.

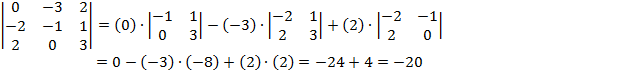
3. Определителем 4-го порядка называется число 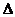, которое определяется, в частности, равенством:

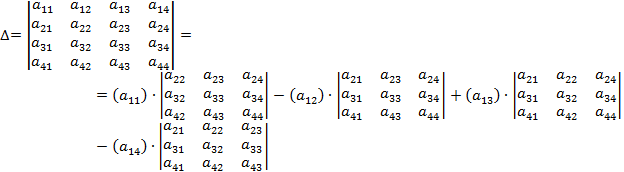
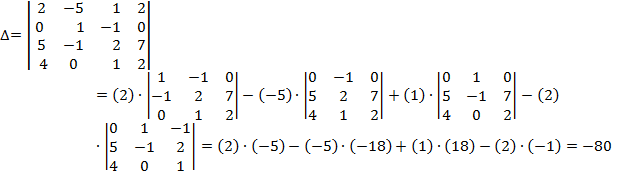
(разложение определителя четвертого порядка по элементам первой строки). Аналогично определитель 4-го порядка можно разложить по элементам других строк или столбцов.

Ответ: 15, -20, -80.

Напомним:

а) что определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:

1) нулей побольше;
2) числа поменьше;

3) .

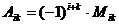б) свойства определителей, которые полезно знать: