Линейные операторы в евклидовом и унитарном пространствах.

Матрица линейного оператора. Собственные значения и собственные векторы. Приведение матрицы линейного оператора к каноническому виду

Матрица линейного оператора.

Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .

В этих пространствах определены базисы e = {e₁, ..., e_n} и f = {f₁, ..., f_m}.

Пусть A(e_i ) = a_1i·f₁ + a_2i·f₂ + ...+ a_mi·f_m — разложение образа i-го базисного вектора базиса e пространства X по базису fпространства Y, i = 1, 2, ..., n.

Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {a_ij}= {A(e_j )_i}:

Координаты образа y = A(x) и прообраза x связаны соотношеннием:

y = A· x,

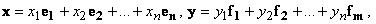
Собственные значения и собственные векторы.

Пусть А - линейный оператор, действующий в линейном пространстве.

Число λ называется собственным значением, а ненулевой вектор х - соответствующим собственным вектором линейного оператора А, если они связаны между собой соотношением Ах= λх .

Пусть А - матрица оператора в некотором базисе.

Собственные значения оператора и соответствующие им собственные векторы связаны соотношением (А- λЕ)х=0 , где Е - единичная матрица, а 0 - нулевой элемент пространства Х. Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы (А- λЕ)х=0, которое существует тогда и только тогда, когда det(А- λЕ)=0 . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения det(А- λЕ)=0 , а собственные векторы - как решения соответствующих однородных систем.

Уравнение det(А- λЕ)=0 называется характеристическим уравнением оператора, а многочлен det(А- λЕ) - характеристическим многочленом оператора.

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:

характеристический многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно λ;

линейный оператор, действующий в n-мерном линейном пространстве имеет не более n различных собственных значений;

собственные векторы, отвечающие различным собственным значениям, линейно независимы;

если линейный оператор, действующий в n-мерном линейном пространстве X, имеет nразличных собственных значений, то собственные векторы оператора образуют базис в пространстве X; этот базис называют собственным базисом оператора;

матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали.

Приведение матрицы линейного оператора к каноническому виду.

Дискретная математика

Булевы функции.

Понятие булевой функции. Основные булевы функции. Таблица истинности. Конъюнктивная и дизъюнктивная начальные формы. Совершенные конъюнктивная и дизъюнктивная начальные формы. Полиномы Жегалкина.

Булевыми значениями (или булевыми константами) называются два заранее выбранных разных символа.Эти два значения могут быть обозначены как угодно.Булевыми переменными называются переменные, которые могут принимать булевы значения.

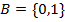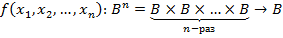Определение булевой функции. Булевой функцией (ф.алгебры логики, двоичной ф. или переключательной ф.) называется всюду определенная на мн-ве ф. , аргум. которой, как и сама ф., принимают значения из двухэлементного мн-ва 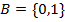. Т.е., булевой ф. от 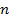переменных 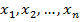называется любая ф. 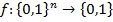, которая произвольному набору 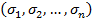нулей и единиц ставит в соотв. свое значение 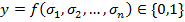, равное 0 или 1. При этом мн-во 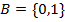называется основным мн-вом или исходным алфавитом переменных, а 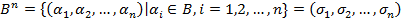, где 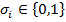. Класс (мн-во) всех булевых функций алгебры логики обозначим через 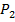или, уточняя, 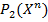, понимая под 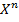мн-во символов переменных .

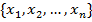Способы задания булевых функций. Поскольку б. ф. являются частным случаем отображений, то для ее задания применяютсяспособызадания отображений:

1)Табличный способ. Булева ф. 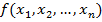полностью определяется своей таблицей истинности, которая имеет вид:

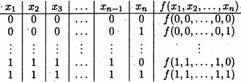
В начале каждой строки таблицы (слева) записывается набор двоичных значений переменных 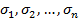а в конце (справа) -значение функции на этом наборе. Чаще всего строки таблицы расположены в лексикографическом порядке (по возрастанию двоичных чисел), при котором в первой строке записан нулевой набор значений переменных 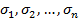а каждый последующий набор получатся из предыдущего прибавлением 1. Тождественно равные ф. имеют, одинаковые таблицы истинности.

Зам: Из таблицы видно, что булева ф. однозначно задается первой и последней сточками. Таблица содержит 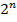строк для двоичных наборов(векторов) значений. Столбец состоит из 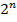наборов нулей и единиц. Всего таких различных столбцов можно построить .

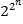2) Векторный способ. При таком представлении б. ф. первый эл. столбца становится первым эл. строки, второй эл. столбца – вторым эл. строки и т.д. В результате для б.ф. 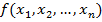получаем строку вида .

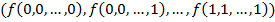3) Графический способ.Мн-во символов переменных 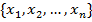будем обозначать 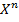, а упорядоченный набор тех же символов 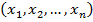через 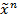.Мн-во всех б.ф. от переменных 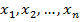будем обозначать через 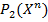. Таким образом, б.ф. от 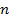переменных 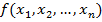произвольному набору из 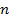нулей и единиц ставит в соответствие 0 или 1. Упорядоченный набор 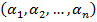, , 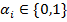состоящий из 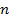нулей и единиц, называется двоичным или булевым вектором (набором).Обознач. 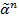или 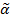. Число 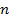называется длиной вектора (набора). Множество всех булевых векторов длины 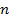называется единичным n-мерным кубом и обозначается 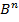. Сами векторы 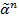называются вершинами куба 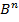. Причём, Число вершин единичного куба

размерности 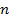, обозначаемое 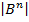, равно .

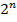4) Представление б.ф. бинарным графом. Наборы 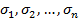нулей и единиц можно представить не только в виде вершин -мерных кубов, но и в виде

вершин так называемого двоичного дерева. Каждая вершина двоичного дерева

представляет собой некоторый набор 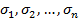нулей и единиц или пустое слово .

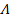5) Аналитический способ задания булевой функции. Это представление б. ф. в дизъюнктивной нормальной форме (ДНФ), совершенной дизъюнктивной нормальной форме (СДНФ), конъюнктивной форме нормальной (КДНФ), совершенной

конъюнктивной нормальной форме (СКНФ) и представление полиномом Жегалкина.

Основные булевы функции.

1)Элементарные булевы функции нулевой местности. Таких функций 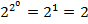. Это константы 0 и 1.

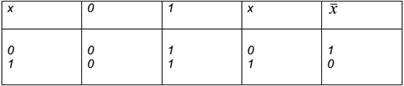
2) Элементарные унарные булевы функции.Сущ. всего 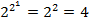б.ф. от одной переменной (унарные булевы функции).

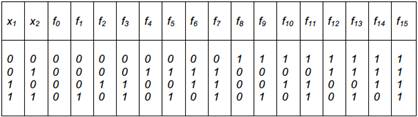
3) Элементарные бинарные булевы функции.Рассматриваем булевы функции двух переменных. Таких функций 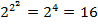. В табл. номера ф. соответствуют номерам двоичных наборов значений соответствующей ф.

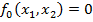­­ – Тождественный ноль. Не зависит от арг. 0-я константа.

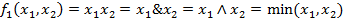–Конъюнкция(«и»), лог. умножение.

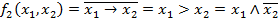–Отрицание импликации 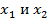(запрет по ).

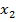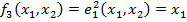–Ф. Выбора первого арг. или селекторная ф.

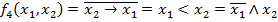–Отрицание импликации 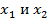(запрет по ).

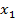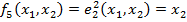–Ф. Выбора второго арг. или селекторная ф.

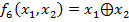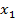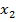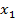-Сумма по модулю два и ( плюс ).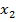

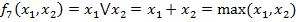-Дизъюнкция(«или»), лог. сумма.

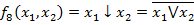-Стрелка Пирса(Лукасевича), или ф. Вебба (антидизъюнкция).

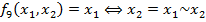-Эквивалентность.

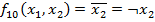-Ф. инверсии второго арг.

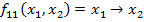-Обратная импликация.

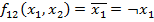-Ф. инверсии первого арг.

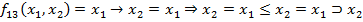-Импликация 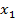и .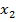

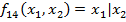-Штрих Шефера или антиконъюкция.

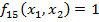-Тождественная единица.

ДНФ,СДНФ. КНФ, СКНФ.

Введѐм обозначени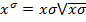е , где 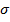-параметр, равный либо 0, либо 1, а 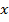-логическая переменная 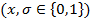.Подставляя различные значения параметра 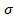получим: 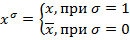. Выражение 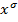называетсялитерой (литералом). Литеры 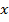и 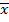называются контрарными.

Опр. Формула вида 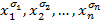, где 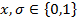, , 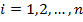а среди переменных 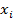могут быть совпадающие, называется элементарной конъюнкцией (ЭК). Элементарная

конъюнкция называется правильной(ПЭК), если всякая переменная входит в нее не более одного раза – включая вхождение под знаком отрицания. Правильная элементарная конъюнкции называется полной (ППЭК) относительно переменных 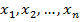, если она

содержит все эти и только эти переменные (может быть под знаком отрицания).Аналогично, формула вида 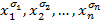называется элементарной дизъюнкцией или дизъюнктом. Пустым дизъюнктом называется константа 0. Дизъюнкт невыполним (то есть, он никогда не равен 1) в том и только в том случае, если он пустой.Элементарная дизъюнкция называется правильной, если в нее каждая переменная входит не более одного раза, включая и вхождения под знаком отрицания. Правильная элементарная дизъюнкция называется полной относительно переменных 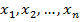если каждая из этих переменных входит в нее один и только один раз.Литералы, составляющие сомножителями.Число сомножителей элементарной конъюнкции (дизъюнкции) называется еѐрангом.

Элементарная конъюнкция или формула вида 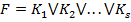, где 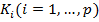элементарные конъюнкции, называется дизъюнктивной нормальной формой (ДНФ). Число 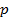называется длиной ДНФ. Сумма рангов входящих в неѐ конъюнкций называется сложностью ДНФ. (Всякая дизъюнкция элементарных конъюнкций называется ДНФ).

Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных 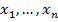называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все

элементарные конъюнкции правильны и полны относительно этих переменных. Говорят, что СДНФ–это ДНФ, удовл. четырем условиям совершенства:1) Все логические слагаемые в формуле различны. 2) Каждое логическое слагаемое содержит все переменные 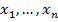, входящие в формулу. 3) Ни одно логическое слагаемое не содержит одновременно переменную 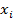и ее отрицание 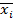. 4) Ни одно логическое слагаемое не содержит одну и ту же переменную 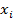дважды.

Элементарная дизъюнкция или формула вида 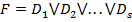, где 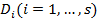элементарные дизъюнкции, называется конъюнктивной нормальной формой (КНФ).Число 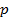называется длинойКНФ. Сумма рангов входящих в неѐ дизъюнкций называется сложностью КНФ. (всякая конъюнкция элементарных дизъюнкций называется КНФ).

Совершенной конъюнктивной нормальной формой (СКНФ)относительно переменных 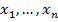называетсяКНФ, в которой нет одинаковых элементарных дизъюнкций и все элементарные дизъюнкции правильны и полны относительно этих переменных.

Говорят, что СКНФ­­–это КНФ, удовл. четырем условиям совершенства: 1) Все логические сомножители (дизъюнкции) в формуле различны. 2) Каждый логический сомножитель содержит все переменные 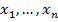входящие в формулу. 3) Ни один логический сомножитель не содержит одновременно переменную 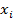и ее отрицание 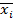. 4) Ни один логический сомножитель не содержит одну и ту же переменную 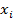дважды.

Полиномы Жегалкина. Полиномом Жегалкина для б.ф. от 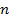переменных называется ее представление в виде полинома, являющегося суммой по модулю 2 константы 0 или 1 и

различных правильных элементарных конъюнкций, в которые все переменные входят в первой степени. Общий вид полинома имеет вид: 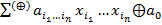. Здесь 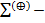означает сумму по модулю 2; суммирование идёт по всем подмн-вам 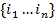мн-ва 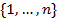, включая пустое подмножество 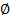. Коэффициенты 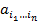принимают значение 0 или 1 (При 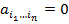соответствующее слагаемое в полиноме опускают). Если все коэффициенты 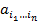, включая 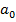равны 0, то полиномпросто записывают как 0.

Примеры полиномов Жегалкина: 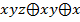; ; 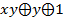; ; 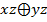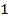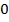. В полиноме Жегалкина константа 0 пишется только тогда, когда другие слагаемыеотсутствуют.