Приложения криволинейных интегралов.

Геометрические Приложения криволинейных интегралов.

1) Длинна кривой.

Пусть 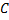является гладкой, кусочно-непрерывной кривой, которая описывается вектором 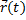, 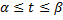. Тогда длина выражается формулой:

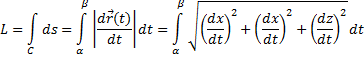
где 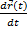– производная, а 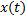, , 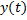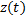– компоненты векторной функции .

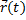Если кривая 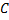представляет собой график заданной явно, непрерывной и дифференцируемой функции 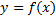, 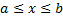в плоскости 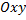, то длина такой кривой вычисляется по формуле:

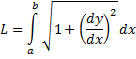
Если кривая 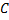задана в полярных координатах уравнением: 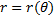, , 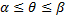и ф. 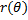является непрерывной и дифференцируемой в интервале 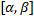, то длина кривой определяется выражением:

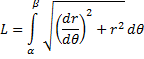
2) Площадь области, ограниченной замкнутой кривой.

Пусть 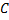является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости 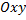. Тогда площадь области R, ограниченной данной кривой, определяется:

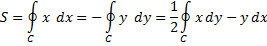
Здесь предполагается, что обход кривой 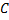производится против часовой стрелки.

3) Объем тела, образованного вращением замкнутой кривой относительно оси .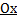

Предположим, что область R расположена в верхней полуплоскости 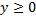и ограничена гладкой, кусочно-непрерывной и замкнутой кривой 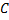, обход которой осуществляется против часовой стрелки. В результате вращения области вокруг оси 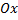образуется тело .

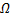Объем данного тела определяется формулами:

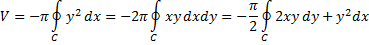
Физические Приложения криволинейных интегралов.

1) Масса кривой.

Предположим, что кусок проволоки описывается некоторой пространственной кривой 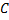. Пусть масса распределена вдоль этой кривой с плотностью 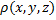. Тогда общая масса кривой выражается через криволинейный интеграл первого рода:

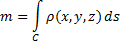
2) Центр масс и моменты инерции кривой.

Пусть снова кусок проволоки описывается некоторой кривой 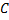, а распределение массы вдоль кривой задано непрерывной функцией плотности .

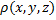Тогда моменты инерции определяются формулами:

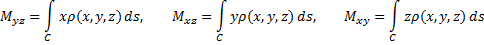
Координаты центра масс кривой определяются формулами:

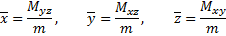
Моменты инерции относительно осей 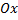, , 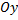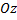определяются формулами:

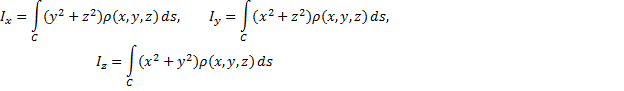
3) Работа поля.

Работа при перемещении тела в силовом поле 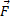вдоль кривой 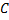выражается через криволинейный интеграл второго рода:

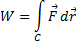
где 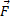– сила, действующая на тело, 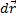– единичный касательный вектор. Обозначение 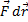означает скалярное произведение векторов 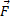и .

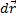4) Закон Ампера.

Криволинейный интеграл от магнитного поля с индукцией 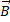вдоль замкнутого контура 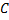пропорционален полному току, протекающему через область, ограниченную контуром C. Это выражается формулой:

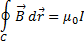
где 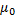– магнитная проницаемость вакуума, равная .

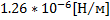5) Закон Фарадея.

Электродвижущая сила 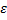, наведенная в замкнутом контуре 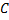, равна скорости изменения магнитного потока 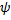, проходящего через данный контур:

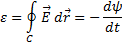
Формула Грина.

Формула Грина связывает двойной и криволинейный интегралы.

Пусть 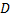– конечная, вообще говоря, многосвязная область на плоскости 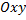с кусочно-гладкой границей 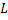(т.е. состоит из конечного числа кусочно-гладких кривых). Область 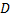с присоединённой границей 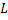обозначим .

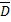Т1.

Пусть ф. 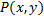и 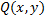непрерывны в 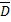и имеют непрерывные частные производные первого порядка в 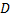. Если 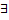несобственные интегралы по области 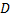от каждой из частных производных ф. 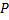и 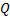, то справедливо соотношение:

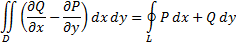
называемое формулой Грина. При этом стоящий в правой части интеграл представляет собой сумму интегралов по связным компонентам границы 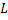, на которых указано такое направление обхода, при котором область 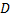остаётся слева.

Формула Стокса.

Формула Стокса обобщение формулы Грина.

Пусть 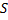– ограниченная, полная, кусочно-гладкая, двусторонняя поверхность с кусочно-гладкой границей 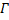. Окрестностью поверхности 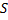будем называть любое открытое множество 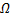, содержащее .

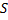Т2.

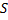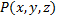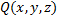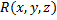Пусть в некоторой окрестности поверхности ф. , , непрерывны и имеют непрерывные частные производные первого порядка. Если 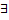несобственные интегралы по области 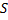от каждой из частных производных ф. 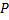, 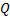и 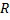, то справедливо соотношение:

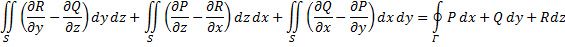
называемое формулой Стокса. При этом стоящий в правой части интеграл представляет собой сумму интегралов по связным компонентам границы 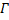, на которых указано такое направление обхода, при котором область 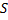остаётся слева.

Формула Остроградского.

Формула связывает тройной интеграл с поверхностным интегралом на границе области.

Пусть 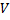– конечная, многосвязная область в пространстве 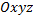с кусочно-гладкой границей 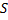. Область 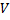с присоединённой границей будем обозначать через .

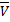Т3.

Пусть ф. 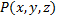, , 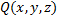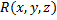непрерывны в 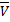и имеют непрерывные частные производные первого порядка в 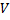. Если 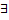несобственные интегралы по области 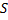от каждой из частных производных ф. 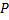, 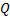и 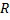, то справедливо соотношение:

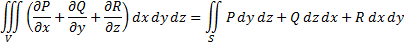
называемое формулой Остроградского. При этом стоящий в правой части интеграл представляет собой сумму интегралов по связным компонентам границы 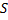, на которых выбрана внешняя по отношению к 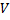сторона.