Опр1.1 ( предел значения ф. одной пер.)

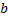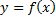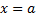Число наз. предельным значением функции в т. (или пределом ф. при ), если для 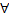сход. послед. значение аргумента 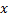, элементы 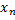которой отличны от , соответствующая послед. значений ф. сходится к .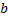

Обозначается так: .

Зам.: функция 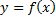может иметь в т. только одно предельное значение. Это вытекает из того, что послед. 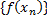может иметь только один предел.

Опр1.2 (предел значения ф. двух пер.)

Число 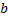наз. предельным значением функции двух переменных при , если для 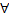числа такая 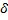– окрестность точки , что для 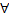точки этой окрестности (за исключением, быть может, точки ) выполняется нерав.:

, или .

Обозначается так: или .

Опр2 (правое (левое) пред. знач. ф.)

Число bназ. правым (левым) предельным значением ф. в т. 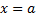, если для любой сход. к послед. значение аргумента 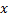, элементы 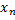которой больше (меньше) , соответствующей послед. значений ф. сходится к b.

Обозначается так: Пр. пред. знач.: или .

Лв. пред. знач.: или .

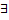Зам.: Если в т. правое и левое предельные значения ф. равны, то в точке а предельное значение этой ф., равное указанным односторонним предельным значениям.

Опр3 (пред. значения ф. при )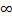

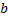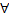Число наз. предельным значением функции при (или пред. ф. при ), если для б.б. послед. значений аргумента соответствующая послед. значений ф. сход. к .

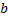Обозначается так: .

Опр4 (пред. значения ф. при )

Число bназ. предельным значением функции при , если для 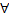б.б. последовательности значений аргумента, элементы которой, начиная с некоторого номера, положительны (отрицательны), соответствуют последовательности значений ф. сход. к .

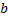Теорема.(Арифм. опер.)

Пусть заданные на одном и том же мн-ве ф. и 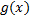имеют в т. предельные значения 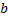и с. Тогда ф. , , имеют в т. пред. знач.: , , соотв.

Док-во.: Пусть –произвольная сходящаяся к послед. значений аргумента ф. и . Соотв. послед. и знач. этих ф. имеют пределы 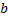и с. Но иногда, в силу теорем сходящихся послед.(см. вопр. 1) послед.: , , имеют пределы, соотв. равные: , , . В силу произвольности послед. 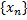это означает, что , , . ч.т.д.

Опр5 (Условие Коши, необх. и дост. условие сущ. пред. знач.)

Будем говорить, что ф. удовлетворяет в т. 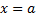условию Коши, если для любого полож. числа ε найдётся полож. число δ такое, что, каковы бы ни были два значения аргумента и , удовлетворяющие неравенствам: , , для соответствующих значений ф. справедливо неравенство: .

Теорема.(Критерий Коши).

Для того чтобы ф. имела конечное предельное знач. в т. 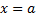, необходимо и достаточно, чтобы ф. удовлетворяла в этой т. условию Коши.

Основные теоремы о пределах.

Т1. (О пред. переходе в равенстве).

Если две ф. принимают одинаковые знач. в окрестности некоторой т., то их пределы в этой т. совпадают. т.е. .

Т2. (О пред. переходе в нерав.)

Если знач. ф. в окрестности некоторой т. не превосходят соответствующие знач. ф. , то предел ф. в этой т. не превосходит предела ф. . т.е.

.

Т3. (Пред. постоянной равен самой постоянной).

.

Т4. (Ф. не может иметь двух различных пред. в одной т.)