Уравнение прямой по точке и направляющему вектору
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение.Каждый ненулевой вектор 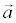 ( α1 , α2 ), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой
( α1 , α2 ), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой
Ах + Ву + С = 0.
Пример. Найти уравнение прямой с направляющим вектором 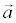 (1, -1) и проходящей через точку А(1, 2). Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
(1, -1) и проходящей через точку А(1, 2). Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
х + у - 3 = 0
Билет5:
Определение.Уравнением линии называется соотношение y = f(x) между координатами точек, составляющих эту линию.
Уравнение прямой на плоскости. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка. Ах + Ву + С = 0,причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.
Теорема.Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как 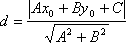 .
.
Билет6:
Окружность— геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Уравнение окружности радиуса R с центром в точке О ( х0 , у 0 ) имеет вид:
( х – х0 ) 2 + ( у – у 0 ) 2 = R 2 .
Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:
х 2 + у 2 = R 2 .
Пусть Р ( х1 , у 1 ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:
( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R 2 .
Условие касания прямой y = m x + k и окружности х 2 + у 2 = R 2 :
k 2 / ( 1 + m 2 ) = R 2
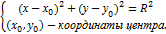
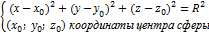
Билет 7:параллельность плоскостей:
2 плоскости являются параллельными, если они не пересекаются и не имеют общих точек.
Св-ва параллельных плоскостей:
1) Если 2 пересекающиеся прямые одной плоскости параллельны 2-ум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
2) Если 2 параллельные плоскости, пересечены 3-ей плоскостью, то линии пересечения их параллельны.
3) Отрезки параллельных прямых, заключённые между параллельными плоскостями равны.
Билет 8:
2 прямые в пространстве называются перпендикулярными; если они пересекаются под углом в 90°.
Прямая называется перпендикуляром к плоскости, если она перпендикулярна любой прямой в этой плоскости:
Теорема:
1) если 1 из 2-ух параллельных прямых перпендикулярна к 3-ей прямой, то и другая прямая перпендикулярна первой.
2) Если 1 из 2-ух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна ей.
3) Если 2 прямые перпендикулярны к плоскости, то они параллельны.
Признак перпендикулярности:
1) если прямая перпендикулярна 2-ум пересекающимся прямым. Лежащим в плоскости, то она перпендикулярна самой плоскости.
2) Через любую точку пространства проходит прямая перпендикулярна к данной плоскости и притом только одна.
Перпендикуляр и наклонная:
Перпендикуляр, проведенный из данной точки к плоскости меньше любой наклонной, проведённый из этой точки этой плоскости.
Теорема:
Прямая, проведённая к плоскости через основание наклонной перпендикулярна к её проекции на этой плоскости, перпендикулярна и самой наклонной. Проекций точки на плоскость называется основанием перпендикуляра, проведённого из точки к плоскости.
Проекций прямой на плоскость не перпендикулярной этой прямой является прямая.
Углом между прямой и плоскостью пересекающую эту прямую называется угол между прямой и её проекцией на плоскости.
Билет 9:
Расстояние от точки до плоскости
Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:
Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.
Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:
A(x – x0) + B(y – y0) + C(z – z0) = 0.
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость. Пусть требуется найти расстояние от точки K до плоскости s (АВС).
О ТРЕХ ПЕРПЕНДИКУЛЯРАХ.
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.
И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Билет 10:
Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.
Пусть плоскость задана уравнением , а прямая - . Из геометрических соображений (см. рис.) видно, что искомый угол a = 90° - j, где a - угол между векторами и .
Билет 11: Декартовы координаты вектора в пространстве
Прямые x, y, z называются координатными осями (или осями координат),
точка их пересечения O – началом координат,
а плоскости xOy, xOz и yOz – координатными плоскостями.
Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.
· Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.
· Единичный вектор, направленный вдоль оси x, обозначается i.
· Единичный вектор, направленный вдоль оси y, обозначается j.
· Единичный вектор, направленный вдоль оси z, обозначается k.
Вектора i, j, k называются координатными векторами.
Любой вектор a можно разложить по координатным векторам: a=xi+yj+zk.
Коэффициенты разложения определяются единственным образом и называются координатами вектора a в данной системе координат.
Билет 12:
Прямые x, y, z называются координатными осями (или осями координат),
точка их пересечения O – началом координат,
а плоскости xOy, xOz и yOz – координатными плоскостями.
Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.
· Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.
· Единичный вектор, направленный вдоль оси x, обозначается i.
· Единичный вектор, направленный вдоль оси y, обозначается j.
· Единичный вектор, направленный вдоль оси z, обозначается k.
Вектора i, j, k называются координатными векторами.
Любой вектор a можно разложить по координатным векторам: a=xi+yj+zk.
Коэффициенты разложения определяются единственным образом и называются координатами вектора a в данной системе координат.
Билет 13
Векторы в пространстве:
Любая точка пространства- это нулевой вектор, его длина равна нулю. Длиной вектора 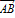 называется длина отрезка. Два не нулевых называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Два вектора
называется длина отрезка. Два не нулевых называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Два вектора 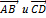 коллинеарные, значит лучи AB и CD со направлены. Если векторы не коллинеарные, то лучи не со направлены, то векторы противоположно направлены. От любой точки пространства можно отложить вектор равный данному и при том только один. Сумма векторов зависит от выбора точки пространства. Для любых векторов
коллинеарные, значит лучи AB и CD со направлены. Если векторы не коллинеарные, то лучи не со направлены, то векторы противоположно направлены. От любой точки пространства можно отложить вектор равный данному и при том только один. Сумма векторов зависит от выбора точки пространства. Для любых векторов 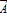 и
и 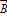 и чисел K и L, выполняются законы:
и чисел K и L, выполняются законы:
1) 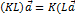 )
)
2) 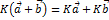
3) 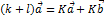
Векторы называются компланарными, если при откладывании их от 1-ой точки они будут лежать в 1-ой плоскости. Любой вектор  можно проложить как
можно проложить как 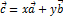 , где х и у единичные отрезки оси Ох и Оу. Если векторы
, где х и у единичные отрезки оси Ох и Оу. Если векторы 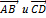 коллинеарны, а векторы
коллинеарны, а векторы  и
и  не коллинеарнв, то вектор
не коллинеарнв, то вектор  можно разложиь по векторам
можно разложиь по векторам  и
и  , причём коэффициенты определяются ед. образом.
, причём коэффициенты определяются ед. образом.
Теорема:
Любой вектор можно разложить по 3-ём данным не коллинеарным векторам, причём коэффициенты расположения определяются ед. способом.
Метод координат в пространстве:
Св-ва векторов:
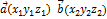
1) 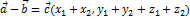
2) 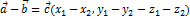
3) 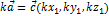
Длина вектора:
1) 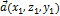
2) 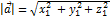
3) 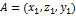
4) 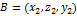
5) 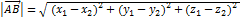
Координаты середины отрезка:
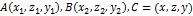 - середины.
- середины.
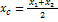 ;
; 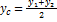 ;
; 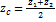 .
.
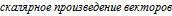 :
:
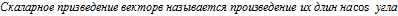 между ними. Это произведение ненулевых векторов равно нулю, тогда и только тогда, эти векторы 1. Скалярный квадрат вектора равен квадрату его длины. Если вектор
между ними. Это произведение ненулевых векторов равно нулю, тогда и только тогда, эти векторы 1. Скалярный квадрат вектора равен квадрату его длины. Если вектор  имеет
имеет 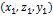 , а
, а 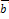 имеет
имеет 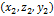 .
.
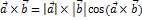
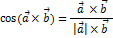
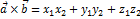
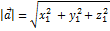
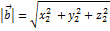
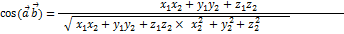
Св-ва векторов
1) 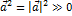
2) 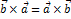
3) 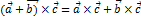
4)K 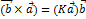
Не нулевой вектор называется направляющим вектором данной прямой, если он лежит на этой прямой или на параллельной прямой.
Движение пространства -это отображение пространства на себе, сохраняющее расстояние между точками.
Движение пространства -это отображение пространства на себе, сохраняющее расстояние между точками.
Центральная симметрия- есть движение.
Осевой симметрией называется отображение пространства на себе при которой точка переходит ей симметричную относительно прямой.
Зеркальная симметрия (симметрия относительно плоскости – это такое отображение пространства на себя при котором каждая точка переходит симметрическую относительно плоскости. Это есть движение.
Билет 14:
Многогранник или полиэдр — поверхность, составленная из многоугольников, которые ограничивают некоторое геометрическое тело, оно также иногда называется многогранником.
Многогранником в трехмерном пространстве называется совокупность конечного числа плоских многоугольников такая, что
каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым по этой стороне;
от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя по очереди от одного многоугольника к другому, смежному с ним.
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.
Площадью поверхности многогранника называется сумма площадей многоугольников, из которых состоит поверхность многогранника, т.е. сумма площадей граней многогранника. Отсюда и решение. У куба 6 граней одного размера, площадь его поверхности равна площади его грани, умноженной на 6.
У параллелограмма тоже 6 поверхностей, по меньшей мере 3 парных. Зная площадь основания и боковых граней, легко узнать его полную площадь.
Билет 15:
Многогранник -часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем, вокруг каждой вершины существует ровно один цикл многоугольников. Эти многоугольники называются гранями, их стороны – ребрами, а вершины – вершинами многогранника. Многогранник называется выпуклым, если он весь лежит по одну сторону от плоскости любой его грани, тогда грани его тоже выпуклы. Выпуклый многогранник разрезает пространство на две части — внешнюю и внутреннюю. Внутренняя его часть есть выпуклое тело. Обратно, если поверхность выпуклого тела многогранная, то соответствующий многогранник — выпуклый.
Билет 16:Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.Условия параллельности и перпендикулярности плоскостейНа основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю.
Билет 17:Призма:Многоугольники, из которых составлен многоугольник называются гранями. Стороны грани, рёбрами. Отрезок соединяющий две вершины, не принадлежащие первому ребру называются диагоналями. Поверхность состав-я из многоугольников и ограничивающая некоторое геометрическое тело называются многогранной поверхностью или многогранником. Многогранник является выпуклым, если он расположен по одну сторону от каждой его грани. Перпендикуляр проведённый из одной точки основания к другому называется высотой. Если рёбра перпендикулярны основаниям, то призма прямая, не перпендикулярны- наклонная. Высота прямой призмы равна его ребру. Призма называется правильной, если её основания правильные многоугольники, а боковые грани равные прямоугольники. Площадь полной поверхности призмы равна сумме боковой поверхности и оснований. Sполн.=Sбок.-2Sосн..Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.
Билет 18:
Параллелепипедом называется призма, в основании которой лежит параллелограмм.
Все грани параллелепипеда — параллелограммы.
Противоположные грани параллелепипеда равны и параллельны. У параллелепипедов и только у них любую пару параллельных граней можно принять за основания.
В зависимости от выбора оснований можно рассмотреть три высоты.
Объем параллелепипеда 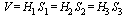
Объём прямоугольного параллелепипеда равен произведению 3-ёх его измерений (ширина, длина, высота) или площадь основания на высоту : V=abc=Sосн.h
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда:
S= 2(Sa+Sb+Sc)= 2(ab+ bc+ ac)
Билет 19:
Тело ограниченное коничеакой поверхностью и кругом называется конусом.
Sпол.=Sбок.+Sосн.
Sбок.=ПRL
Sосн.=П 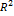
Sпол.= П 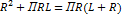
Объем конуса равен одной третьей части произведения высоты конуса h на площадь основания конуса.
Площадь основания конуса можно определить по следующей формуле: 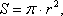
Тогда формулу для вычисления объема конуса можно записать в следующем виде: 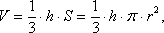
Билет 20:
Апофема- перпендикуляр, проведённый из вершин к любой стороне основания или высота любой грани. Высота пирамиды- перпендикуляр проведённый из вершины к плоскости основания. Пирамида является правильной, если в основании правильный многоугольник. Боковые грани- равные равнобедренные треугольники Sпол.=Sбок.+Sосн.
Выпуклый многоугольник называется правильным, если его грани равные многоугольники. Правильный тетраэдр составлен из 4-х равносторонних треугольников; Сумма плоских углов при каждой вершине равна 180 градусов. Правильный октаэдр составлен из 8 равносторонних треугольников. Сумма плоских углов при каждой вершине равна 240 градусов. Правильный икосаэдр составлен из 20 равносторонних треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Правильный додекаэдр составлен из 12 равносторонних5-тиугольников. Сумма плоских углов при каждой вершине равна 324 градуса. Куб составлен из 6-ти кв-ов сумма углов равна 270 градусов.
Билет 21:
Отрезки прямых заключённые между параллельными окружностями образуют цилиндрическую поверхность. Эти отрезки называют образующими. Sбок. Поверхности = ПRL; Sосн.= П 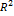 . (Sпол.)=Sбок.+ 2 осн.параллельные круги называются основаниями.
. (Sпол.)=Sбок.+ 2 осн.параллельные круги называются основаниями.
Билет 22:
Сфера:
Это поверхность состоящая из точек пространства, расположенных на одном расстоянии от данной точки. Это расположение называется радиусом сферы.
Плоскость, имеющая со сферой (шаром) одну общую точку, называется касательной плоскостью, более одной общей точки — секущей плоскостью. Прямая, имеющая со сферой одну общую точку, называется касательной прямой, две общие точки — секущей прямой. Пусть ρ (O; а) — расстояние от центра шара (сферы) с центром О и радиусом R до плоскости а.
Если ρ > R, то шар (сфера) и плоскость общих точек не имеют.
Сечение шара плоскостью, проходящей через центр шара (ρ = 0), называется большим кругом шара.
Эта плоскость является плоскостью симметрии шара и делит его на две равные части (два полушария). Признак касательной плоскости
Если плоскость проходит через конец диаметра сферы и перпендикулярна ему, то эта плоскость касательная к сфере.
Если ρ = R, плоскость и шар (сфера) имеют одну общую точку.
Плоскость касается шара (сферы). Свойство касательной плоскости
Плоскость, касательная к сфере, перпендикулярна диаметру (радиусу), проходящему через точку касания. Признак касательной прямой
Если прямая проходит через конец диаметра сферы и перпендикулярна ему, то эта прямая касательная к сфере.
