Функция распределения и ее свойства
Следующей характеристикой распределения вероятностей случайной величины, которую можно применить для разнообразных случайных величин, в отличие от ряда распределения, который применим только для дискретных случайных величин, является функция распределения.
Функцией распределения, или интегральным законом распределения случайной величины X, называется задание вероятности выполнения неравенства X < x, рассматриваемой как функции аргумента x:
(2.9)
Функция распределения характеризует полностью случайную величину с вероятностной точки зрения.
Определение функции распределения имеет простую геометрическую интерпретацию. Если рассматривать случайную величину как случайную точку X оси OX (рис. 2.1), которая в результате опыта может занять то или иное местоположение, то функция распределения F(x) есть вероятность того, что случайная точка X в результате опыта попадает левее точки x.
|
Рис. 2.1
Для дискретной случайной величины X, если возможные значения ее 
, функция распределения будет иметь вид:
(2.10)
где символ 
под знаком суммы обозначает, что суммирование распространяется на все возможные значения случайной величины, которые по своей величине меньше аргумента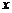 
.
Формулу (2.10) можно записать в виде:
(2.11)
Таким образом,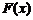 
для дискретной случайной величины разрывная и возрастает скачками при переходе через точки 
.
Пример 1.Дан ряд распределения случайной величины X:
| X |
| |||||
| p | 0,4 | 0,1 | 0,3 | 0,2 |
Найти и изобразить графически ее функцию распределения.
Р е ш е н и е. По условию:
Построим с помощью выражения (2.11) функцию распределения:
Изобразим 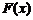графически, как показано на рис. 2.2.
Рассмотрим основные свойства функции распределения:
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
Справедливость этого свойства следует из того, что функция распределения – это вероятность.
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. при 
:
Пусть a и b – точки числовой оси, причем . Рассмотрим два несовместных события 
тогда 
. Это соотношение между событиями видно из их геометрической интерпретации (рис. 2.3).
|
А = (х < a)
Рис. 2.3
По теореме сложения для несовместных событий:
или
откуда
(2.12)
Так как 
, то 
, т.е. 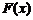– неубывающая функция.
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице, т.е.:
Действительно:
4. Вероятность попадания случайной величины X в интервал 
равна приращению ее функции распределения на этом интервале, т.е.:
(2.13)
Формула (2.13) следует непосредственно из формулы (2.12).
Пример 2. Функция распределения случайной величины X имеет вид:
Найти вероятность того, что случайная величина примет значение в интервале (1;3).
Р е ш е н и е. По формуле (2.13):
Для нахождения значений используем заданную функцию распределения.