Понятие определителя. Свойства определителей

Совокупность 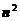чисел, расположенных в виде таблицы, называется определителем 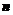-го порядка. Для определителя используются следующие обозначения:

.

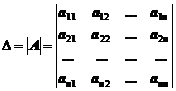Числа 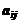называются элементами определителя. Первый индекс 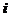обозначает номер строки, второй индекс 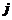обозначает номер столбца. Порядок определителя равен числу строк. У определителя число строк всегда равно числу столбцов. Определитель является числом.

Определитель первого порядка содержит один элемент и равен ему

.

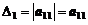Определитель второго порядка вычисляется по следующему правилу

.

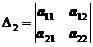
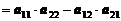Определитель третьего порядка можно вычислить по следующей схеме, добавив к определителю первые два столбца:

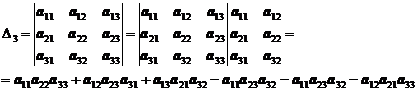
Определители высших порядков вычисляются с помощью свойств определителей.

Свойства определителей

1. Определитель не изменится, если в нем строки и столбцы поменять местами.

2. Определитель изменит только знак, если в нем поменять местами какие-нибудь две строки или два столбца.

3. Общий множитель элементов строки или столбца можно выносить за символ определителя.

4. Если все элементы какой-нибудь строки или столбца равны нулю, то определитель равен нулю.

5. Определитель равен нулю, если элементы двух строк или столбцов пропорциональны.

6. Определитель равен нулю, если он имеет две одинаковых строки или два одинаковых столбца.

7. Если все элементы некоторой строки или столбца состоят из двух слагаемых, то определитель можно представить в виде суммы двух определителей, в одном из которых элементами соответствующей строки являются первые слагаемые, во втором - вторые. Например:

.

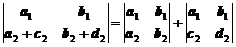8. Если к элементам некоторого столбца или строки определителя прибавить соответствующие элементы другого столбца или строки, умноженные на любой общий множитель 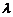, то величина определителя не изменится. Например:

.

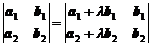Следующее свойство позволяет понижать порядок определителя. Оно формулируется с помощью понятия алгебраического дополнения.

Алгебраическим дополнением 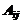элемента 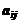называется произведение 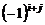на определитель, который получается вычеркиванием в данном определителе строки и столбца, на пересечении которых стоит элемент .

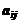9. Определитель равен сумме произведений элементов какого-нибудь столбца или строки на их алгебраические дополнения (теорема Лапласа). Например:

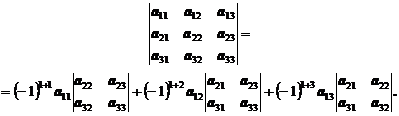
С помощью этого свойства вычисление определителя 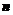-го порядка приводится к вычислению определителей 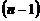-го порядка. Эта процедура называется разложением определителя по элементам строки или столбца.

Пример 1. Упростить определитель и вычислить его:

.

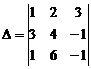Прежде, чем вычислять определитель, можно упростить его, пользуясь свойствами определителей. В данном примере можно выполнить следующие действия: умножим элементы 1-го столбца на 2 и вычтем из элементов 2-го столбца, затем умножим элементы 1-го столбца на 3 и вычтем из элементов 3-го столбца. Тогда получим

.

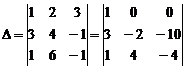Теперь можно легко вычислить этот определитель, разложив его по элементам 1-ой строки:

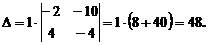
Пример 2. Разложить определитель по элементам 2-ой строки.

.

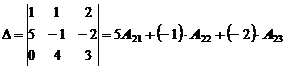Учитывая определение алгебраического дополнения, получим

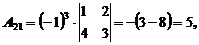
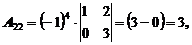
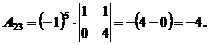
Теперь вычисляем определитель: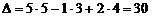

Система линейных уравнений

Линейные уравнения - это уравнения, в которых переменные имеют только первую степень и нет произведения переменных.

Система 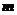линейных уравнений с 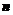неизвестными записывается в виде:

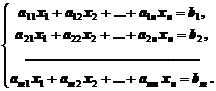(1)

В частном случае число уравнений и число переменных совпадают.

Решением системы является совокупность 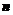чисел, которые при подстановке их в уравнения (1) обращают их в тождество.

Если система (1) имеет хотя бы одно решение, она называется совместной; если нет ни одного решения, то система несовместна.

Если совместная система имеет только одно решение, то она называется определенной. Если более одного решения, то неопределенной.

Если определитель системы не равен нулю 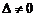, то система имеет единственное решение. Для решения системы 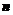- линейных уравнений с 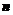- неизвестными существует несколько методов.

Метод Крамера

При использовании этого метода решение системы находится по формулам

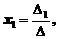
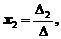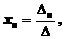..., (2)

здесь 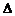-определитель системы, 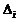- определитель, в котором элементы 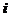-го столбца определителя системы заменяются соответствующими свободными членами уравнений системы.

При решении системы следует иметь в виду следующее:

1. Если 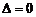, но хотя бы один из определителей 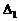, , 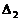..., 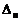не равен нулю, то система несовместна.

2. Если 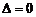и все определители 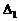, , 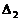..., 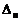равны нулю, то система или несовместна или имеет бесконечно много решений, если существует хотя бы одно решение.

Пример 3. Решить систему уравнений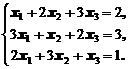

Найдем определитель системы:

.

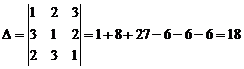Найдем вспомогательные определители

.

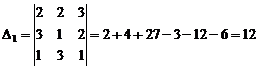Аналогично находим

, .

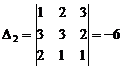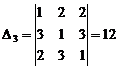Теперь по формулам Крамера (2) найдем переменные

, , .

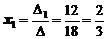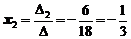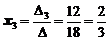Матричный метод решения

Рассмотрим этот метод на примере системы трех линейных уравнений:

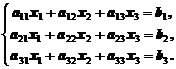
эту систему можно представить в матричной форме:

,

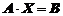где

, , .

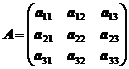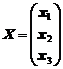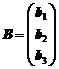Как видно, А это матрица, составленная из коэффициентов при перемененных, В - матрица - столбец из свободных членов уравнений, Х - матрица - столбец из переменных.

Решая матричное уравнение, находим

,

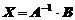где 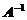- обратная матрица.

Итак, чтобы найти решение системы, нужно найти обратную матрицу 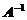и умножить ее на матрицу В.

Пример 4. Решить систему матричным способом

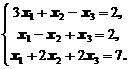
Найдем определитель системы: .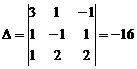

Составим матричное уравнение: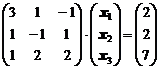

Найдем обратную матрицу. Для этого сначала найдем алгебраические дополнения:

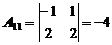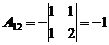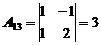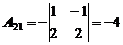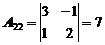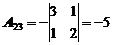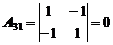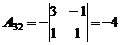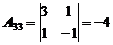Построим обратную матрицу:

.

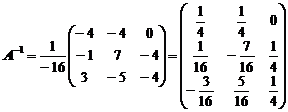Теперь найдем произведение матриц:

.

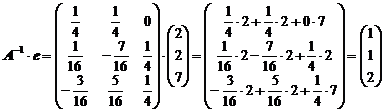Итак, имеем .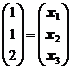

Отсюда, , , .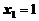

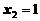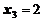Метод Гаусса

Этот метод решения системы линейных уравнений заключается в последовательном исключении переменных из уравнений для того, чтобы в одном из уравнений осталось одно неизвестное. Покажем, как применяется этот метод на примере.

Пример 5. Решить систему уравнений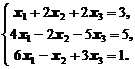

Для удобства преобразований, составим расширенную матрицу из коэффициентов и свободных членов:

.

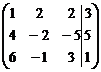Умножим 1-ую строку на (-4) и сложим со второй строкой; затем умножим 1-ую строку на (-6) и сложим с третьей, получим

.

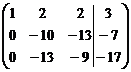Теперь умножим 2-ую строку на 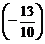и сложим с третьей; получим

.

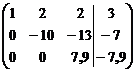Запишем полученные преобразованные уравнения:

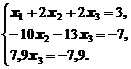
Теперь из 3-его уравнения находим 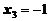, из 2-го уравнения находим 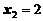, из 1-го уравнения имеем 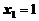. Итак, решение системы , , .

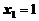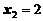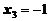Как видно из данного примера, преобразования уравнений нужно делать так, чтобы элементы матрицы, расположенные ниже диагонали оказались равны нулю.