Смысл и определение индекса множественной корреляции.

Показатель множественной корреляции характеризует тесноту рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

,

где s²_y – общая дисперсия результативного признака;

s_ост² – остаточная дисперсия для уравнения у = ¦(х_1,х₂,….,x_p).

Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

При правильном включении факторов в регрессионной анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции.

При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

(3.8)

где - стандартизованные коэффициенты регрессии;

- парные коэффициенты корреляции результата с каждым фактором.

39. Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса).

Индекс корреляции - нормированный показатель тесноты связи. Коэффициент индекса корреляции показывает долю общей вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющей переменной.Чем ближе индекс корреляции к 1 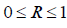, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

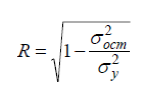
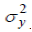общая дисперсия результативного признака y,

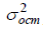остаточная дисперсия, определяемая по уравнению нелинейной регрессии.

Тест Бокса – Кокса. При сравнении моделей с использованием в качестве зависимой переменной y и ln_y проводится такое преобразование масштаба наблюдений y, при котором можно непосредственно сравнивать СКО в линейной и логарифмической моделях. Выполняются следующие шаги:

• Вычисляется среднее геометрическое значений y в выборке. Оно совпадает с экспонентой среднего арифметического логарифмов y.

• Все значения y пересчитываются делением на среднее геометрическое, получаем значения y*.

• Оцениваются две регрессии:

- для линейной модели с использованием y* в качестве зависимой переменной;

- для логарифмической модели с использованием ln_y* вместо ln_y.

Во всех других отношениях модели должны оставаться неизменными. Теперь значения СКО для двух регрессий сравнимы, и модель с меньшей остаточной СКО обеспечивает лучшее соответствие исходным данным.

• Для проверки, обеспечивает ли одна из моделей значимо лучшее соответствие, можно вычислить величину (n/2)lnz,

где z – отношение значений остаточной СКО в перечисленных регрессиях.

Эта статистика имеет распределение хи – квадрат с одной степенью свободы. Если она превышает критическое значение при выбранном уровне значимости α, то делается вывод о наличии значимой разницы в качестве оценивания. Величина коэффициента эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 %