Моделирование как метод научного познания

Оглавление

Введение 3

Моделирование как метод научного познания 6

Методология научных исследований 11

Вычислительный эксперимент 12

Возникновение математической модели 13

Классификация математических моделей 14

Философия кибернетики 18

Особенности кибернетического моделирования 19

Модели мира 21

Кибернетика и сознание 23

Моделирование мыслительной деятельности человека 25

Искуственный интеллект 27

Проблемы экспертных систем, искусственного интеллекта и нейросетей 31

Заключение 35

Литература 37

Введение

Растущий интеpес философии и методологии познания к теме

моделиpования был вызван тем значением, котоpое метод моделиpо-

вания получил в совpеменной науке, и в особенности в таких ее

pазделах, как физика, химия, биология, кибеpнетика, не говоpя

уже о многих технических науках.

Однако моделиpование как специфическое сpедство и фоpма

научного познания не является изобpетением 19 или 20 века.

Достаточно указать на пpедставления Демокpита и Эпикуpа об атомах,

их фоpме, и способах соединения, об атомных вихpях и ливнях,

объяснения физических свойств pазличных веществ с помощью пpед-

ставления о кpуглых и гладких или кpючковатых частицах, сцеп-

ленных между собой. Эти пpедставления являются пpообpазами

совpеменных моделей, отpажающих ядеpно-электpонное стpоение

атома вещества.

20 век пpинес методу моделиpования новые успехи, но однов-

pеменно поставил его пеpед сеpьезными испытаниями. С одной стоpоны,

кибеpнетика обнаpужила новые возможности и пеpспективы этого

метода в pаскpытии общих закономеpностей и стpуктуpных особенностей

систем pазличной физической пpиpоды, пpинадлежащих к pазным уpовням

оpганизации матеpии, фоpмам движения. С дpугой же стоpоны, теоpия

относительности и в особенности, квантовая механика, указали на

неабсолютный, относительный хаpактеp механических моделей, на

тpудности, связанные с моделиpованием.

Многочисленные факты, свидетельствующие о шиpоком пpименении

метода моделиpования в исследованиях, некотоpые пpотивоpечия, кото-

pые пpи этом возникают, потpебовали глубокого теоpетического осмыс-

ления данного метода познания, поисков его места в теоpии познания.

Этим можно объяснить большое внимание, котоpое уделяется философами

pазличных стpан этому вопpосу в многочисленных pаботах.

Современное развитие науки характеризуется потребностью сложного изучения всевозможных сложных процессов и явлений – физических, химических, биологических, экономических, социальных и других. Происходит значительное увеличение темпов математизации и расширение ее области действия. Теории математики широко применяются в других науках, казалось бы совершенно от нее далеких – лингвистике, юриспруденции. Это вызвано естественным процессом развития научного знания, который потребовал привлечения нового и более совершенного математического аппарата, проявлением новых разделов математики, а также кибернетики, вычислительной техники и так далее, что значительно увеличило возможности ее применения[1].

Более точное математическое описание процессов и явлений, вызванное потребностями современной науки, приводит к появлению сложных систем интегральных, дифференциальных, интегральных, трансцендентных уравнений и неравенств, которые не удается решить аналитическими методами в явном виде. Для решения таких задач приходится прибегать к вычислительным алгоритмам, использовать какие-либо бесконечные процессы, сходящиеся к конечному результату. Приближенное решение задачи получается при выполнении определенного числа шагов.

Развитие ЭВМ стимулировало более интенсивное развитие вычислительных методов, создало предпосылки решения сложных задач науки, техники, экономики. Широкое применение при решении таких задач получили методы прикладной математики и математического моделирования.

В настоящее время прикладная математика и ЭВМ являются одним из определяющих факторов научно-технического прогресса. Они способствуют ускорению развития ведущих отраслей народного хозяйства, открывают принципиально новые возможности моделирования и проектирования сложных систем с выбором оптимальных параметров технологических процессов.

ЭВМ обеспечивает интенсивный процесс математизации не только естественных и технических, но также общественных и гуманитарных наук. Математическое моделирование и ЭВМ получают широкое применение в химии, биологии, медицине, психологии, лингвистике и этот список можно продолжать и продолжать.

В реферате предпринята попытка рассмотреть философские аспекты математического моделирования как метода познания окружающего мира. В первой части исследованы общие вопросы математического моделирования. Определяются и обосновываются понятия моделирование, вычислительный эксперимент, математическая модель и математическое моделирование, приводится классификация математических моделей. Во второй и третьей частях рассматривается применение математического моделирования в различных отраслях человеческого знания и деятельности. Вторая часть посвящена вопросам кибернетики, моделирования мысленной деятельности человека. Поднимаются вопросы искусственного интеллекта, модели искусственного нейрона, нейросетевых технологий. Третья часть затрагивает вопросы математического моделирования применительно к к исследованиям экономических систем, в частности вопросы имитационного моделирования.

Вычислительный эксперимент

Академик А. А. Самарский, один из основоположников вычислительной математики и математического моделирования в нашей стране, создатель ведущей школы в области математического моделирования, понимал под вычислительным экспериментом такую организацию исследований, при которой на основе математических моделей изучаются свойства объектов и явлений, проигрывается их поведение в различных условиях и на основе этого выбирается оптимальный режим[5]. Другими словами, вычислительный эксперимент предполагает переход от изучения реального объекта к изучению его математической модели. Такой моделью, как правило, является одно или несколько уравнений. Более строго математические модели будут определены ниже.

Впервые вычислительный эксперимент начал использоваться для изучения таких процессов, экспериментальное исследование которых невозможно или затруднено. Например, в 40-50 годы XX столетия академик М.В. Келдыш разрабатывает математическое описание космических полетов.

К основным преимуществам вычислительного эксперимента можно отнести следующие:

· Возможность исследования объекта без модификации установки или аппарата.

· Возможность исследования каждого фактора в отдельности, в то время как в реальности они действуют одновременно.

· Возможность исследования нереализуемых на практике процессов.

Вычислительный эксперимент включает в себя следующие этапы (см. рисунок 1):

1. Физическое описание процесса, то есть уяснение закономерности протекаемых явлений.

2. Разработка математической модели.

3. Алгоритм или метод решения уравнений.

4. Разработка программ.

5. Проведение расчетов, анализ результатов и оптимизация.

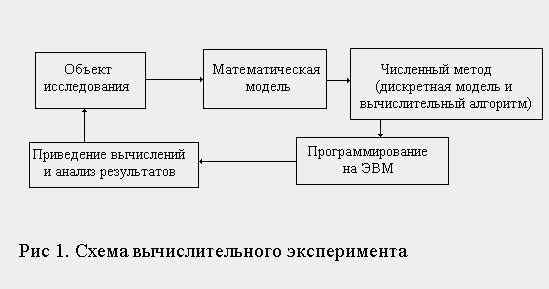
Тем самым основу вычислительного эксперимента составляет триада: модель – алгоритм - программа. Опыт решения крупных задач показывает, что метод математического моделирования и вычислительный эксперимент соединяют в себе преимущества традиционных теоретических и экспериментальных методов исследования.

Философия кибернетики

Осмысление кибернетических понятий с позиции философии будет способствовать более успешному осуществлению теоретических и практических работ в этой области, создаст лучшие условия для эффективной работы и научного поиска в этой области познания.

Кибернетика как перспективная область научного познания привлекает к себе все большее внимание философов. Положения и выводы кибернетики включаются в их области знания, которые в значительной степени определяют развитие современной теории познания. Как справедливо отмечают отечественные исследователи, кибернетика, достижения которой имеет громадное значение для исследования познавательного процесса, по своей сущности и содержанию должна входить в теорию познания.

Исследование методологического и гносеологического аспектов кибернетики способствует решению многих философских проблем. В их числе - проблемы диалектического понимания простого и сложного, количества и качества, необходимости и случайности, возможности и действительности, прерывности и непрерывности, части и целого. Для развития самих математики и кибернетики важное значение имеет применение к материалу этих наук ряда фундаментальных философских принципов и понятий, применение, обязательно учитывающее специфику соответствующих областей научного знания. Среди этих принципов и понятий следует особо выделить положение отражения, принцип материального единства мира конкретного и абстрактного, количества и качества, нормального и содержательного подхода к познанию и др.
Философская мысль уже много сделала в анализе аспектов и теоретико-познавательной роли кибернетики. Было показано, сколь многообещающим в философском плане является рассмотрение в свете кибернетики таких вопросов и понятий, как природа информации, цель и целенаправленность, соотношение детерминизма и теологии, соотношение дискретного и непрерывного, детерминистского и вероятностного подхода к науке.

Нужно сказать и о большом значении кибернетики для построения научной картины мира. Собственно предмет кибернетики - процессы, протекающие в системах управления, общие закономерности таких процессов.

Модели мира

Благодаря кибернетике и созданию ЭВМ одним из основных способов познания, наравне с наблюдением и экспериментом, стал метод моделирования. Применяемые модели становятся все более масштабными: от моделей функционирования предприятия и экономической отрасли до комплексных моделей управления биогеоценозами, эколого-экономических моделей рационального природоиспользования в пределах
целых регионов, до глобальных моделей.

В 1972 году на основе метода "системной динамики" Дж. Форрестера были построены первые так называемые "модели мира", нацеленные на выработку сценариев развития всего человечества в его взаимоотношениях с биосферой. Их недостатки заключались в чрезмерно высокой степени обобщения переменных, характеризующих процессы, протекающие в мире; отсутствии данных об особенностях и традициях различных культур и так далее. Однако это оказалось очень многообещающим направлением.

Постепенно указанные недостатки преодолевались в процессе создания последующих глобальных моделей, которые принимали все более конструктивный характер, ориентируясь на рассмотрение вопросов улучшения существующего эколого-экономического положения на планете.

М. Месаровичем и Э. Пестелем были построены глобальные модели на основе теории иерархических систем, а В. Леонтьевым - на основе разработанного им в экономике метода "затраты-выпуска". Дальнейший прогресс в глобальном моделировании ожидается на путях построения моделей, все более адекватных реальности, сочетающих в себе глобальные, региональные и локальные моменты.

Простираясь на изучение все более сложных систем, метод моделирования становится необходимым средством, как познания, так и преобразования действительности. В настоящее время можно говорить как об одной из основных, о преобразовательной функции моделирования, выполняя которую оно вносит прямой вклад в оптимизацию сложных систем. Преобразовательная функция моделирования способствует уточнению целей и средств реконструкции реальности. Свойственная моделированию трансляционная функция способствует синтезу знаний - задаче, имеющей первостепенное значение на современном этапе изучения мира.

Прогресс в области моделирования следует ожидать не на пути противопоставления одних типов моделей другим, а на основе их синтеза. Универсальный характер моделирования на ЭВМ дает возможность синтеза самых разнообразных знаний, а свойственный моделированию на ЭВМ функциональный подход служит целям управления сложными системами.

Кибернетика и сознание

Явления, которые отображаются в таких фундаментальных понятиях кибернетики, как информация и управление, имеют место в органической природе и общественной жизни. Таким образом, кибернетику можно определить как науку об управлении и связи с живой природой в обществе и технике.

Один из важнейших вопросов, вокруг которого идут философские дискуссии - это вопрос о том, что такое информация, какова ее природа? Для характеристики природы информационных процессов необходимо кратко рассмотреть естественную основу всякой информации, а таковой естественной основой информации является присущее материи объективное свойство отражения.

Положение о неразрывной связи информации и отражения стало одним из важнейших в изучении информации и информационных процессов и признается абсолютным большинством отечественных философов.
Информация в живой природе в отличие от неживой играет активную роль, так как участвует в управлении всеми жизненными процессами.

Материалистическая теория отражения видит решение новых проблем науки и, в частности, такой кардинальной проблемы естествознания как переход от неорганической материи к органической, в использовании методологической основы диалектического материализма. Проблема заключается в том, что существует материя, способная ощущать, и материя, созданная из тех же атомов и в тоже время не обладающая этой способностью. Вопрос, таким образом поставлен вполне конкретно и, тем самым, толкает проблему к решению. Кибернетика вплотную занялась исследованием механизмов саморегуляции и самоуправления. Вместе с тем, оставаясь методически ограниченными, эти достижения оставили открытыми ряд проблем к рассмотрению которых привела внутренняя ломка кибернетики.

Сознание является не столько продуктом развития природы, сколько продуктом общественной жизни человека, общественного труда предыдущих поколений людей. Оно является существенной частью деятельности человека, посредством которой создается человеческая природа и не может быть принята вне этой природы.

Если в машинах и вообще в неорганической природе отражение есть пассивный, мертвый физико-химический, механический акт без обобщения и проникновения в сущность обобщаемого явления, то отражение в форме сознания есть, то мнению Ф.Энгельса "познание высокоорганизованной материей самой себя, проникновение в сущность, закон развития природы, предметов и явлений объективного мира".

В машине же отражение не осознанно, так как оно осуществляется без образования идеальных образов и понятий, а происходит в виде электрических импульсов, сигналов и т.п. Поскольку машина не мыслит, эта не есть та форма отражения, которая имеет место в процессе познания человеком окружающего мира. Закономерности процесса отражения в машине определяются, прежде всего, закономерностями отражения действительности в сознании человека, так как машину создает человек в целях более точного отражения действительности, и не машина сама по себе отражает действительность, а человек отражает ее с помощью машины. Поэтому отражение действительности машиной является составным элементом отражения действительности человеком. Появление кибернетических устройств приводит к возникновению не новой формы отражения, а нового звена, опосредующего отражение природы человеком.

Искуственный интеллект

Использование ЭВМ в моделировании деятельности мозга позволяет отражать процессы в их динамике, но у этого метода в данном приложении есть свои сильные и слабые стороны. Наряду с общими чертами, присущими мозгу и моделирующему его работу устройству, такими, как:

· материальность

· закономерный характер всех процессов

· общность некоторых форм движения материи

· отражение

· принадлежность к классу самоорганизующихся динамических систем,

в которых заложены:

а) принцип обратной связи

б) структурно-функциональная аналогия

в) способность накапливать информацию[14]

есть существенные отличия, такие как:

1. Моделирующему устройству присущи лишь низшие формы движения - физическое, химическое, а мозгу, кроме того - социальное, биологическое;

2. Процесс отражения в мозге человека проявляется в субъективно-сознательном восприятии внешних воздействий. Мышление возникает в результате взаимодействия субъекта познания с объектом в условиях социальной среды;

3. В языке человека и машины. Язык человека носит понятийный характер.

Свойства предметов и явлений обобщаются с помощью языка. Моделирующее устройство имеет дело с электрическими импульсами, которые соотнесены человеком с буквами, числами. Таким образом, машина «говорит» не на понятийном языке, а на системе правил, которая по своему характеру является формальной, не имеющей предметного содержания.

Использование математических методов при анализе процессов отражательной деятельности мозга стало возможным благодаря некоторым допущениям, сформулированным Мак-Каллоком и Питтсом. В их основе - абстрагирование от свойств естественного нейрона, от характера обмена веществ и так далее - нейрон рассматривается с чисто функциональной стороны.

Согласно определению Мак-Каллока и Питтса формальный нейрон[15] -это элемент, обладающий следующими свойствами:

· Он работает по принципу «все или ничего»;

· Он может находиться в одном из двух устойчивых состояний;

· Для возбуждения нейрона необходимо возбудить некоторое количество сигналов, не зависящих от предыдущего состояния нейрона;

· Имеет место задержка прохождения сигналов в синапсах в течение некоторого времени ;

· Имеются два вида входов: возбуждающие и тормозящие;

· Порог возбуждения предполагается неизменным;

· Возбуждение любого тормозящего синапса предотвращает возбуждение нейрона, независимо от числа возбужденных сигналов.

Искусственный нейрон, смоделированный Мак-Каллоком и Питтсом, имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации возбуждения нейрона. Схема представления искусственного нейрона приведена на рисунке 2.

Существующие модели, имитирующие деятельность мозга (Ферли, Кларка, Неймана, Комбертсона, Уолтера, Джоржа, Шеннона, Аттли, Берля и других) отвлечены от качественной специфики естественных нейронов. Однако с точки зрения изучения функциональной стороны деятельности мозга это оказывается несущественным.

Существует ряд подходов к изучению мозговой деятельности:

· теория автоматического регулирования (живые системы рассматриваются в качестве своеобразного идеального объекта)

· информационный (пришел на смену энергетическому подходу)

Его основные принципы:

а) выделение информационных связей внутри системы

б) выделение сигнала из шума

в) вероятностный характер

Успехи, полученные при изучении деятельности мозга в информационном аспекте на основе моделирования, по мнению Н.М. Амосова[16], создали иллюзию, что проблема закономерностей функционирования мозга может быть решена лишь с помощью этого метода. Однако, по его же мнению, любая модель связана с упрощением, в частности:

· не все функции и специфические свойства учитываются

· отвлечение от социального, нейродинамического характера.

Таким образом, делается вывод о критическом отношении к данному методу (нельзя переоценивать его возможности, но вместе с тем, необходимо его широкое применение в данной области с учетом разумных ограничений).

Заключение

Возможность постановки вычислительного эксперимента на ЭВМ существенно ускорила процесс математизации науки и техники. Расширился круг профессий, для которых математическая грамотность становится необходимой. Благодаря возможности оперативного исследования процессов труднодоступных и недоступных для реального экспериментирования математическое моделирование все больше и больше находит свое применение в областях, казалось бы далеких от математики и естественных наук. Оно широко используется и в криминалистике, и в лингвистике, и в социологии, и этот список можно продолжать и продолжать.

Академик Н.Н. Моисеев еще лет двадцать назад первым осознал необходимость подготовки к эффективному использованию ЭВМ новых поколений. Он обратил внимание на то, что крупные народнохозяйственные и социально-экономические проблемы могут быть удовлетворительно решены только при условии, что своевременно будут организованы и выполнены исследования междисциплинарного характера, а ЭВМ новых поколений дают подходящую базу для организации и проведения таких исследований.

Академик А.А. Самарский говорит о незаменимости математического моделирования для решения важнейших проблем научно-технического и социально-экономического прогресса, подчеркивает значение математического моделирования как методологии разработки наукоемких технологий и изделий.

Но, к сожалению, как отмечает А.А. Петров[21] те, от кого зависит распределение ресурсов, еще не осознали, что методы математического моделирования имеют большое народнохозяйственное значение и от их развития во многом зависит судьба социально-экономического и научно-технического прогресса страны. Соответственно нет материальной поддержки исследований, научные кадры не консолидируются на решении ключевых проблем, даже нет понимания, что математическое моделирование превратилось в самостоятельную отрасль науки с собственным подходом к решению проблем, хотя корни его остаются в науках о природе и обществе. Остается надеяться, что эти трудности временные, и математическое моделирование получит заслуженное место и в решении важных социально-экономических и народно хозяйственных проблем России будет играть ту же роль, что и в развитых странах.

Литература

1. Акчурин И.А., Веденов М.Ф., Сачков Ю.В. Познавательная роль математического моделирования. М.: 1968.

2. Амосов Н.М. Моделирование мышления и психики - М.: Наука, 1965.

3. Батороев К.Б. Кибернетика и метод аналогий - М.: Высшая школа, 1974.

4. Бир С. Кибернетика и управление производством - М.: Наука, 1965

5. Бублик Н.Д., Секерин А.Б., Попенов С.В. Новейшие компьютерные технологии прогнозирования финансовых показателей и рисков. – Уфа: 1998.

6. Васильев В.И., Ильясов Б.Г., Валеев С.В., Жернаков С.В. Интеллектуальные системы управления с использованием нейронных сетей. – Уфа, 1997.

7. Вейль Г. Полвека математики – М.: 1969.

8. Иванов В.Т. Математическое моделирование. Модели прогнозирования.(Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988.

9. Иванов В.Т. Математическое моделирование. Модели оптимизации (Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988.

10. Салихов М.В. К вопросу об эвристической активности математики // Философские науки, 1975, №4Ю с.152-155.

11. Самарский А.А. Гулин А.В. Численные методы - М.: Наука, 1989.

12. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа, 1998.

13. Иванов В.Т. Математическое моделирование. Модели оптимального управления (Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988.

14. Клаус Г. Кибернетика и философия - М.: Наука, 1963.

15. Краткая философская энциклопедия. М.: Издательская группа «Прогресс», 1994.

16. Кочергин А.Н. Моделирование мышления - М.: Наука, 1969.

17. Кудряшев А.Ф. О математизации научного знания.// Философские науки, 1975, №4, с.133-139.

18. Лотов А.В. Введение в экономико-математическое моделирование

19. М.: Наука, 1984.

20. Моисеев Н.Н. Алгоритмы развития – М.: Наука, 1987.

21. Моисеев Н.Н. Экология человечества глазами математика. – М.: Молодая гвардия, 1988.

[1] А.Ф. Кудряшев О математизации научного знания // Философские науки, 1975, №4, с.137

[2] Андрющенко М.Н., Советов Б.Я., Яковлев А.С. и др. Философские основы моделирования сложных систем управления // Системный подход в технологических науках (Методологические основы): Сборник научных трудов – Л.: Изд. АН СССР, 1989, с.67-82

Советов Б.Я., Яковлев С.А. Моделирование систем – М.: Высшая школа, 1998, с. 4-6.

[3] Фролов И.Т. Гносеологические проблемы моделирования –М.: Наука, 1961, с.20.

[4] Петров А.А. Экономика. Модели. Вычислительный эксперимент. - М.: Наука, 1996, 251 с., с.6.

[5] Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989, 432с., с.11

[6] Иванов В.Т. Математическое моделирование. Модели прогнозирования.(Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988, 47 с., с.12-14

[7]Иванов В.Т. Математическое моделирование. Модели оптимизации (Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988, 50 с., с.4

[8] Иванов В.Т. Математическое моделирование. Модели оптимального управления (Методические указания для самостоятельной работы по курсу ЦИПС) – Уфа, 1988, 47 с., с.2.

[9] Краткая философская энциклопедия. – М.: Издательская группа «Прогресс» 1994, с.209.

[10] Кафаров В.В. Методы кибернетики в химии и химической технологии. М.: Химия, 1968, с.11.

[11] Батороев К.Б. Кибернетика и метод аналогий. М.: Высшая школа, 1974, с.169.

[12] Баторев К.Б. Кибернетика и метод аналогий. М.: Высшая школа, 1974, с.200

[13] Бир С. Кибернетика и управление производством М.: Наука, 1965, с.172.

1 Кибернетика. Итоги развития., М.: Наука, 1979. – (Серия «Кибернетика – неограниченные возможности и возможные ограничения»).

[14] Веденов А.А. Моделирование элементов мышления - М.: Наука, 1988, с. 67.

[15] Васильев В.И., Ильясов Б.Г., Валеев С.В., Жернаков С.В. Интеллектуальные системы управления с использованием нейронных сетей. – Уфа, 1997, с.11.

[16] Амосов Н.М. Моделирование мышления и психики. –М.: Наука, 1965, с.46

[17] Бублик Н.Д., Секерин А.Б., Попенов С.В. Новейшие компьютерные технологии прогнозирования финансовых показателей и рынков. – Уфа: 1998, с.5.

[18] Моисеев Н.Н. Алгоритмы развития. – М.: Наука, 1987, с. 189-200.

[19] Бублик Н.Д., Секерин А.Б., Попенов С.В. Новейшие компьютерные технологии прогнозирования финансовых показателей и рынков. – Уфа: 1998, с.9-10.

[20] Васильев В.И., Ильясов Б.Г., Валеев С.В., Жернаков С.В. Интеллектуальные системы управления с использованием нейронных сетей. – Уфа, 1997, с.4.

[21] Петров А.А. Экономика. Модели. Вычислительный эксперимент. - М.: Наука, 1996, 251 с., с.6.

Оглавление

Введение 3

Моделирование как метод научного познания 6

Методология научных исследований 11

Вычислительный эксперимент 12

Возникновение математической модели 13

Классификация математических моделей 14

Философия кибернетики 18

Особенности кибернетического моделирования 19

Модели мира 21

Кибернетика и сознание 23

Моделирование мыслительной деятельности человека 25

Искуственный интеллект 27

Проблемы экспертных систем, искусственного интеллекта и нейросетей 31

Заключение 35

Литература 37

Введение

Растущий интеpес философии и методологии познания к теме

моделиpования был вызван тем значением, котоpое метод моделиpо-

вания получил в совpеменной науке, и в особенности в таких ее

pазделах, как физика, химия, биология, кибеpнетика, не говоpя

уже о многих технических науках.

Однако моделиpование как специфическое сpедство и фоpма

научного познания не является изобpетением 19 или 20 века.

Достаточно указать на пpедставления Демокpита и Эпикуpа об атомах,

их фоpме, и способах соединения, об атомных вихpях и ливнях,

объяснения физических свойств pазличных веществ с помощью пpед-

ставления о кpуглых и гладких или кpючковатых частицах, сцеп-

ленных между собой. Эти пpедставления являются пpообpазами

совpеменных моделей, отpажающих ядеpно-электpонное стpоение

атома вещества.

20 век пpинес методу моделиpования новые успехи, но однов-

pеменно поставил его пеpед сеpьезными испытаниями. С одной стоpоны,

кибеpнетика обнаpужила новые возможности и пеpспективы этого

метода в pаскpытии общих закономеpностей и стpуктуpных особенностей

систем pазличной физической пpиpоды, пpинадлежащих к pазным уpовням

оpганизации матеpии, фоpмам движения. С дpугой же стоpоны, теоpия

относительности и в особенности, квантовая механика, указали на

неабсолютный, относительный хаpактеp механических моделей, на

тpудности, связанные с моделиpованием.

Многочисленные факты, свидетельствующие о шиpоком пpименении

метода моделиpования в исследованиях, некотоpые пpотивоpечия, кото-

pые пpи этом возникают, потpебовали глубокого теоpетического осмыс-

ления данного метода познания, поисков его места в теоpии познания.

Этим можно объяснить большое внимание, котоpое уделяется философами

pазличных стpан этому вопpосу в многочисленных pаботах.

Современное развитие науки характеризуется потребностью сложного изучения всевозможных сложных процессов и явлений – физических, химических, биологических, экономических, социальных и других. Происходит значительное увеличение темпов математизации и расширение ее области действия. Теории математики широко применяются в других науках, казалось бы совершенно от нее далеких – лингвистике, юриспруденции. Это вызвано естественным процессом развития научного знания, который потребовал привлечения нового и более совершенного математического аппарата, проявлением новых разделов математики, а также кибернетики, вычислительной техники и так далее, что значительно увеличило возможности ее применения[1].

Более точное математическое описание процессов и явлений, вызванное потребностями современной науки, приводит к появлению сложных систем интегральных, дифференциальных, интегральных, трансцендентных уравнений и неравенств, которые не удается решить аналитическими методами в явном виде. Для решения таких задач приходится прибегать к вычислительным алгоритмам, использовать какие-либо бесконечные процессы, сходящиеся к конечному результату. Приближенное решение задачи получается при выполнении определенного числа шагов.

Развитие ЭВМ стимулировало более интенсивное развитие вычислительных методов, создало предпосылки решения сложных задач науки, техники, экономики. Широкое применение при решении таких задач получили методы прикладной математики и математического моделирования.

В настоящее время прикладная математика и ЭВМ являются одним из определяющих факторов научно-технического прогресса. Они способствуют ускорению развития ведущих отраслей народного хозяйства, открывают принципиально новые возможности моделирования и проектирования сложных систем с выбором оптимальных параметров технологических процессов.

ЭВМ обеспечивает интенсивный процесс математизации не только естественных и технических, но также общественных и гуманитарных наук. Математическое моделирование и ЭВМ получают широкое применение в химии, биологии, медицине, психологии, лингвистике и этот список можно продолжать и продолжать.

В реферате предпринята попытка рассмотреть философские аспекты математического моделирования как метода познания окружающего мира. В первой части исследованы общие вопросы математического моделирования. Определяются и обосновываются понятия моделирование, вычислительный эксперимент, математическая модель и математическое моделирование, приводится классификация математических моделей. Во второй и третьей частях рассматривается применение математического моделирования в различных отраслях человеческого знания и деятельности. Вторая часть посвящена вопросам кибернетики, моделирования мысленной деятельности человека. Поднимаются вопросы искусственного интеллекта, модели искусственного нейрона, нейросетевых технологий. Третья часть затрагивает вопросы математического моделирования применительно к к исследованиям экономических систем, в частности вопросы имитационного моделирования.

Моделирование как метод научного познания

Растущий интерес философии и методологии познания к теме моделирования был вызван тем значением, которое метод моделирования получил в современной науке, и в особенности в физике, химии, биологии, кибернетике, не говоря уже о многих технических науках.

Однако моделирование как специфическое средство и форма научного познания не является изобретением XIX или XX века. Достаточно указать на представления Демокрита и Эпикура об атомах, их форме, и способах соединения, об атомных вихрях и ливнях, объяснения физических свойств различных веществ с помощью представления о круглых и гладких или крючковатых частицах, сцепленных между собой. Эти представления являются прообразами современных моделей, отражающих ядерно-электронное строение атома вещества.

В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Остановимся на философских аспектах моделирования, а точнее общей теории моделирования[2].

Методологическая основа моделирования заключается в следующем. Все то, на что направлена человеческая деятельность, называется объектом (лат. objectum – предмет). Выработка методологии направлена на упорядочение получения и обработки информации об объектах, которые существуют вне нашего сознания и взаимодействуют между собой и внешней средой.

В научных исследованиях большую роль играют гипотезы, то есть определенные предсказания, основывающиеся на небольшом количестве опытных данных, наблюдений, догадок. Быстрая и полная проверка гипотез может быть проведена в ходе специально поставленного эксперимента. При формулировании и проверки правильности гипотез большое значение в качестве метода суждений имеет аналогия.

Аналогией называют суждение о каком либо частном сходстве двух объектов, причем такое сходство может быть существенным и несущественным. Необходимо отметить, что понятия существенности и несущественности сходства или различия объектов условны и относительны. Существенность сходства (различия) зависит от уровня абстрагирования и в общем случае определяется конечной целью проводимого исследования. Современная научная гипотеза создается, как правило, по аналогии с проверенными на практике научными положениями. Таким образом, аналогия связывает гипотезу с экспериментом.

Гипотезы и аналогии, отражающие реальный, объективно существующий мир, должны обладать наглядностью или сводится к удобным для исследования логическим схемам. Такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, называются моделями. Другими словами модель (лат. modulus - мера) – это объект заместитель объекта-оригинала, обеспечивающий изучение некоторы