В рамках системного подхода при решении задачи синтеза
В рамках системного подхода при решении задачи синтеза
обычно руководствуются следующими принципами и приемами:
1. Сочетание декомпозиции, композиции и иерархичности.
2. Выделение нескольких этапов создания системы, фиксирующих
переход на новый уровень рассмотрения.
3. Всестороннее рассмотрение взаимодействия системы с элемента-
ми внешней среды.
4. Всестороннее рассмотрение основных видов взаимодействия
внутри системы между ее элементами.
5. Сочетание различных качественных и количественных методов
исследования.
6.Генетический анализ и учет предыстории развития данного класса
систем
7. Учет возможности изменения исходных данных и даже содержа-
ния решаемой задачи в ходе многоэтапного процесса создания системы.
Перечисленные принципы и подходы составляют основу эволюционной технологической схемы процесса реального синтеза сложной
Системы.
Она базируется на введении иерархии слоев – уровней сложности
принятия решений в условиях априорной неопределенности, в рамках
которых фиксируются промежуточные параметры решения общей задачи
по частям и которая содержит:
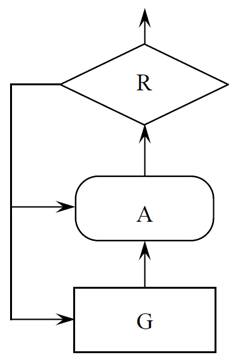
1. Слой выбора (генерации) множества неопределенностей и альтернативных стратегий
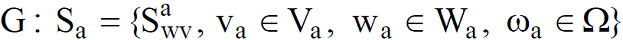
2. Слой обучения или адаптации
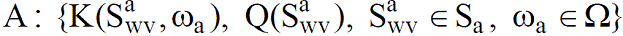
3. Слой самоорганизации
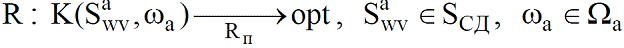
2. Типы отношения подобия систем и моделей. Имитационная модель: основные этапы разработки.
Модели классифицируются по типам реализуемых в них отношений подобия.Эти отношения должны обеспечивать, с одной стороны,подобиев рассматриваемом аспекте исследования, а, с другой стороны,максимальную степень независимостипо отношению к не рассматриваемым аспектам.
Абстрактная (закрытая) система– не имеет физических каналов связи с внешней средой.
Физическая (реальная) системавзаимодействует тем или иным образом с внешней средой и доступна наблюдению.
Четыре типа отношений моделирования – четыре типа моделей в зависимости от природы исходной и моделирующей ее системы.
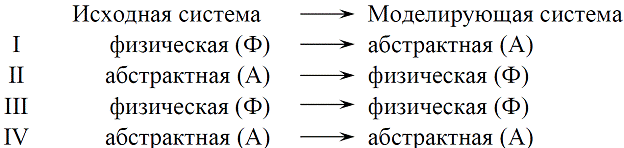
Имитационная модель (ИМ)− это формальное (то есть выполненное на некотором языке) описание логики функционирования исследуемой системы и взаимодействия ее элементов во времени, учитывающеенаиболее существенные причинно-следственные связи, присущие системе, и обеспечивающее проведение статистических экспериментов.
Имитационная модель позволяет разрешить главную проблему современной науки − проблему сложностиили, как еще говорят, − «проклятие размерности».
Существо процесса имитационного моделирования сводится к следующим основным фазам.
1. Построение математического описания процессов и подпроцессов преобразования информации в системе, состоящего из совокупности аналитических моделей различного характера и используемого формализма.
Системы.
2. Построение набора алгоритмов, обеспечивающих имитацию всех подпроцессов в соответствии с составляющими математической модели и с логикой причинно-следственных связей, имеющей место в реальной системе.
Моделирующим алгоритмом.
3. Реализация на ЭВМ программы имитации и статистического анализа эффективности системы, ее отладка, тестирование и эксплуатация.
Модельное время вводится для синхронизации последовательности событий, происходящих в модели системы, и организации «квазипараллелизма» при имитации одновременного функционирования компонентов системы.
Теорема.
Пустьслучайная величинаαимеет равномерное распределение винтервале [0, 1]и связана со случайной величиной ξ соотношением
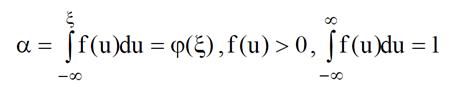
где f (u) – некоторая функция, удовлетворяющая указанным свойствам.
Тогдаслучайная величинаξимеет плотность распределения вероятностей вида f (u) и может быть найдена на основе обратного функционального преобразования
Для доказательства найдем функцию распределения ξ. Используем тот факт, что при f (u) > 0 величинаα монотонно возрастающая функция ξ.
Также и ξ в этом случае монотонно возрастающая функция α. Тогда для функции распределения ξ выполняется следующая цепочка равенств:
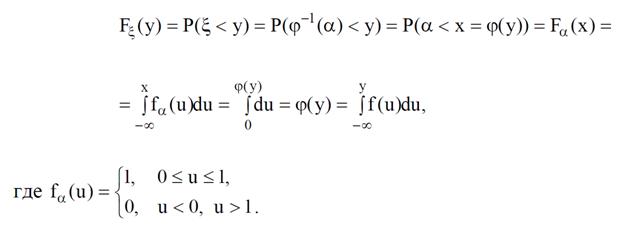
| Очевидно, что Fξ(y) = ϕ(y) , что и требовалось доказать, так как это | |||
| означает, что ξ имеет плотность распределения вида f (u)(fξ(u) = f (u)). | |||
| Таким образом,последовательность случайных чиселξiс таким | |||
| распределением можно получить из соотношения вида | |||
 | |||
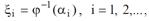где αi− последовательность значений РСВ, получаемых при обращении к датчику α.
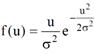Пример. Пусть− закон Релея. Тогда
 |
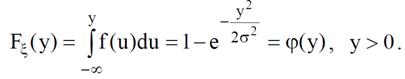Функциональная связь величин ξ и α определяется соотношением
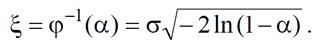
При непосредственной генерации можно использовать более экономное соотношение
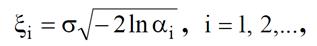
так как величина 1−α также имеет равномерное распределение на интервале [0, 1].
Метод исключений (метод Фон-Неймана).Особенностью данногометода является то, что он может использоваться для генерации величин, заданных как аналитическим видом закона распределения, так и эмпирически полученными распределениями.
Теорема.
Пустьфункцияg(x)≥0и на ее основе определено множество значений вещественных переменных G ={(x, y), 0 ≤ y ≤ g(x)}.
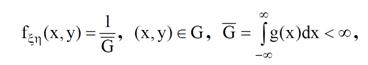
Пустьсовместная плотность распределения случайных величинξиη на множестве значений G равна
то есть имеет равномерный вид.
 |
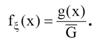Тогдаплотность распределения вероятностей случайной величиныξ равна
 |
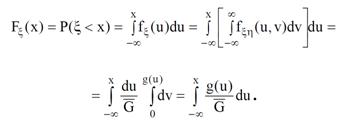Учтем, что для функции распределения ξ выполняется
Отсюда следует доказательство теоремы, так как
 |
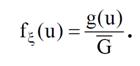Математическая модель объекта в данном случае практически полностью определяет и его моделирующий алгоритм, который в ЭВМ сводится к реализации процедуры численного или аналитического интегрирования обыкновенного дифференциального уравнения.
Задание вероятностных автоматов может быть проведено в табличном виде или в виде графов, дополненных соответствующими значениями ненулевых вероятностей переходов и выходов.
Имитационное моделирование элементов, описываемых на основе P-схем, реализуется на основе алгоритма, определяющего все возможные переходы в соответствии с математической моделью и включающего также процедуру генерации случайной составляющей переходов для соответствующих вероятностей.
Математическая схема стохастического конечно-разностного уравнения
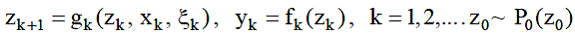
Математическая модель широко используется для описания элементов систем и сетей массового обслуживания потоков событий (заявок) в связи и телефонии, а также для любых информационно-управляющих систем, которые могут рассматриваться как совокупность тем или иным способом соединенных ЭПО.
Построение имитационных моделей с использованиемQ-схем имеет специфику и для разработки моделирующего алгоритма требуется использование специальных подходов и методов.
Математическая схема стохастического дифференциального уравнения
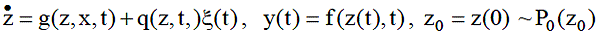
12.Математическая модель взаимодействия элементов сложной системы. Формирование одноуровневой схемы сопряжения.
В качестве математической схемы информационного взаимодействия необходимо рассматривать вторую составляющую механизма обмена сигналами – схему сопряжения элементов, определяющую адресацию характеристик выходных сигналов одних элементов и их компоновку во входные сигналы других элементов.
Математической схемой сопряжения элементов в системеS называется совокупность<X, Y, R >, а операторR называется оператором сопряжения.
Схема сопряжения<X, Y, R >содержит исчерпывающие сведения о модели взаимодействия и соединении элементов сложной системы.
Такая схема называется одноуровневойв том смысле, что она определяет прямое сопряжение элементов без учета их объединения в подсистемы или функциональные модули.
13.Основные типы систем массового обслуживания. Аналитическое решения для СМО М/М/1/0.
В ходе математической формализации систем как систем или сетей массового обслуживания (СМО) они традиционно представляются в виде композиции элементарных приборов обслуживания (Q-схем), соединенных в соответствии с имеющимися взглядами на облик системы.
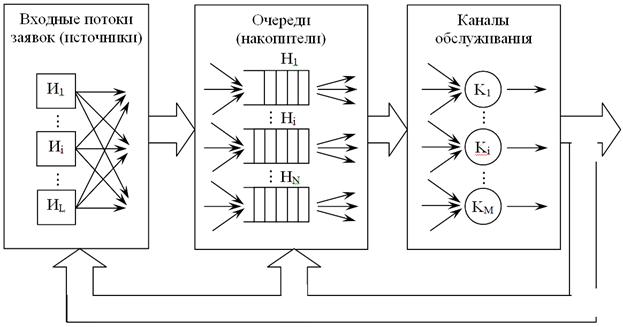
Обобщенная структурная схема СМО
Все СМО делятся на два больших класса:
разомкнутые СМО – функционирование источников и входной поток не зависят от процесса обслуживания (обратной связи нет);
замкнутые СМО –входной поток зависит от числа заявок, находящихся на обслуживании, а заявки с выхода могут опять поступать на вход системы (существует обратная связь).
Другие признаки классификации СМО:
1. По отсутствию или наличию возможности ожидания заявок в очередях выделяют: СМО с отказами; СМО с ожиданием; СМО смешанного типа, имеющие ограничения на время ожидания или на размеры очереди.
2. По количеству параллельно включаемых элементарных приборов обслуживания различают одноканальные и многоканальные СМО.
3. По числу этапов – фаз обслуживания заявок входного потока, реализуемых при последовательно включенных элементарных приборах обслуживания, выделяют однофазные и многофазные СМО.
4. По наличию специальных правил обслуживания различают СМО с приоритетными дисциплинами и бесприоритетными дисциплинами обслуживания (типа FIFO, LIFO).
Для определения СМО применяется специальная символика:
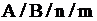
где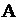 
– вид входного потока заявок или распределения интервалов между ними; 
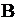– вид потока обслуживания или распределения длительности обслуживания; 
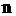– количество обслуживающих каналов; 
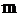– предельная длина очереди ( 
).
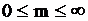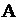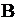Символы и/или принимают различные обозначения и определяют вид входного потока и потока обслуживания:
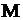– поток является пуассоновским и интервалы времени между заявками (событиями) имеют экспоненциальное распределение.
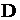– поток является детерминированными интервалы времени между событиями постоянны;
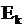– поток являетсяэрланговским ( 
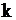-го порядка)и интервалы времени между заявками имеют распределение Эрланга( 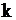-го порядка);
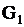– поток общего видас произвольным законом распределения интервалов времени между заявками (событиями).
Аналитической моделью СМОназывается совокупность уравнений и формул, позволяющих определять вероятности состояний системы в процессе ее функционирования в зависимости от времени и рассчитывать значения показателей эффективности по заданным параметрам входящего потока и потоков каналов обслуживания.
Рассмотрим примерпостроения такой модели для марковской одноканальной СМО с отказами типа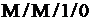
.Одной из возможных интерпретаций такой системы массового обслуживания является одноканальная телефонная линия.
На вход системы поступает пуассоновский поток заявок с интенсивностью
,
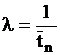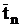– средний интервал времени между входящими заявками.
Каждая поступившая заявка обслуживается в течение времени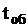 
(длительность разговора), распределенного по показательному закону. Интенсивность пуассоновского потока обслуживания равна
.
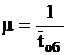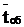– среднее время обслуживания заявки.
Требуется по известным значениям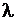 
, 
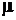определить вероятность обслуживания заявки в любой момент времени 
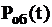, вероятность отказа в обслуживании 
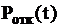, относительную 
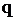и абсолютную 
пропускные способности системы.
При построении аналитических моделей СМО на основе уравнений Колмогорова используют визуальное представление системы в виде графа с вершинами, отвечающими состоянием СМО, и дугами, соответствующими разрешенным переходам.
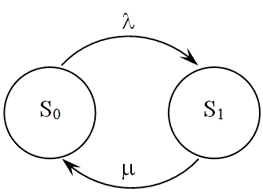
Графы состояний и переходов для систем массового обслуживания М/М/1/0
СМО вида 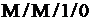может находиться в одном из двух состояний:
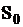– канал обслуживания свободен;
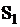– канал обслуживания занят.
Для любого момента времени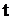 
, 
.
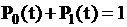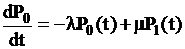
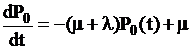Интегрирование последнего уравнения при начальном условии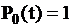 
дает решение
,
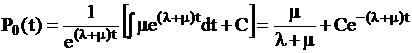где C-константа. С учетом начальных условий можно получить
, 
, 
.
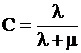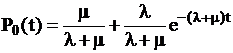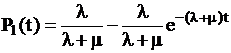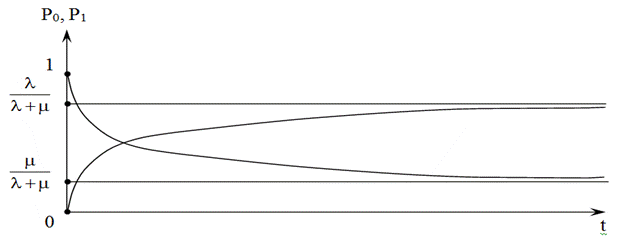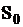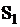Зависимости вероятностей пребывания СМО в состояниях и от времени
Вероятность обслуживания заявки, поступившей в момент времени 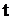равна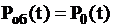 
, вероятность отказа в обслуживании равна 
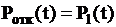, относительная пропускная способность системы равна 
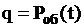, абсолютная пропускная способность равна 
.
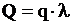При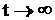 
СМО переходит в установившейся режим работы
, 
.
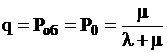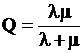14.Сущность метода имитационного моделирования применительно к исследованию СМО. Потоки событий и их характеристики (1,2,3,7).
Реализация технологий имитационного моделирования применительно к задачам исследования СМО предполагает:
1) построение алгоритмов и программных модулей, вырабатывающих реализации случайных потоков однородных и неоднородных событий – «генераторов» источников;
2) построение моделирующих алгоритмов и программных модулей, описывающих функционирование отдельных элементов, а также СМО в целом в соответствии с ее структурой и внутренними параметрами;
3) многократное воспроизведение входных потоков и общего процесса обслуживания, а также обработку получаемых данных в интересах оценки показателей эффективности данного типа СМО.
Элементы СМО разделяют на активные, пассивные и активно-пассивные.
Активными элементами называются такие, смена состояний которых обусловлена только их внутренними свойствами.
Пассивныминазываются такие элементы, которые изменяют свои свойства только под воздействием активных элементов, а, в общем случае, любых внешних факторов.
Активно-пассивными элементами называются такие, которые в одном из своих возможных состояний являются активными, а в других – пассивными.
Активные элементы – источники заявок.
Пассивные элементы – накопители заявок.
Активно-пассивные элементы – каналы обслуживания заявок.
Простейший поток
Поток, для которого одновременно выполняются свойстваординарности, отсутствия последействия, стационарности называется простейшим.
Простейший поток занимает центральное место в теории СМО.Для простейшего потока
, 
,
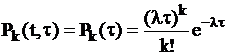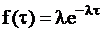имеет место пуассоновский закон распределения числа событий и показательный закон распределения интервалов между событиями.
Важность простейшего (пуассоновского) потока обусловлена следующим: согласно предельной теореме сумма большого числа независимых потоков с произвольным законом распределения интервалов между событиями стремится к простейшему с ростом числа слагаемых.
Поток Пальма
Поток Пальма характеризуется свойствами стационарности, ординарности и ограниченного последействия. Важными для практики образцами потока Пальма являются потоки Эрланга различных порядков.
Потоком Эрланга порядка 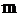называется поток, образуемый из простейшего в результате «просеивания» последнего, когда выбрасываются все точки за исключением 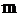-ой. Для такого потока закон распределения интервалов имеет вид
,
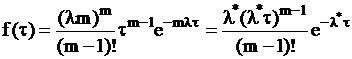где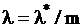 
– интенсивность потока Эрланга, а 
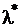– интенсивность исходного потока Пуассона. Простейший поток является частным случаем потока Эрланга при 
.
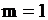I.Генерация входных потоков
Случайным потоком называется последовательность событий, следующих одно за другим в некоторые, вообще говоря, случайные моменты времени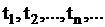 
При построении генераторов случайных потоков следует, прежде всего, определить тип потока событий, который требуется воспроизвести.
1.Однородность–неоднородность
Однородный поток – характеризуется только моментами наступления событий (вызывающими моментами) и задается случайной последовательностью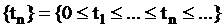 
, где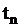 
– момент наступления 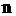-го события (неотрицательное вещественное число).
Однородный поток также может быть задан в виде случайной последовательности интервалов времени между событиями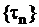 
, 
( 
, 
).
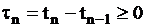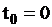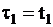Неоднородный поток – характеризуется случайной последовательностью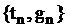 
, где 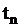– вызывающие моменты, а 
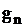– набор признаков события, изменяющихся по детерминированному или случайному закону в зависимости от .
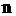Ординарность–неординарность
Ординарный поток событий –характеризуется тем, что вероятность выпадения более одного события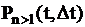 
за малый интервал времени величиной 
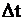в окрестности точки 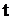пренебрежимо мала по сравнению с вероятностью выпадения ровно одного события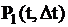 
, 
, 
.
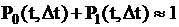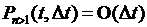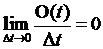События, как правило, происходятпо отдельности, без образования сгустков.
Неординарный поток, характеризуется тем, что вероятность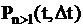 
не равна нулю.
Гибридные автоматы (ГА)
Гибридный автоматопределяется как граф системы переходов, в которой каждой вершине ствится в соответствие область пространства состояний системы, характеризующая её непрерывное поведение в промежутках между событиями, приводящими к смене поведения. Этим событиям соответствуют дуги системы переходов.
1.Используются в современных инструментальных средствах визуального моделирования динамических (реактивных) систем.
2.Для гибридного автомата, как и для любой непрерывно-дискретной системы, глобальное поведение описывается последовательностью локальных поведений, смена которых проходит под воздействием событий.
3.Наступление того или иного события зависит от значений непрерывных параметров, а, следовательно, от функций локального поведения.
4.Каждое событие может порождать другие события, а дискретный процесс, результатом которого может быть выбор нового локального поведения, описывается в общем случае нетривиальным алгоритмом.
5.Поведение системы можно представить последовательностью сменяющих друг друга длительных непрерывных и мгновенных дискретных поведений.
6.В математическом плане ГА объединяет язык дифференциальных уравнений и язык конечных автоматов в единый формализм, по своим возможностям весьма напоминающий формализм А-схем.
Примером ГА является система, описываемая в пространстве состояний следующим уравнением:
, 
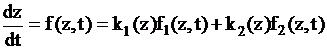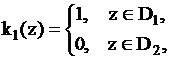
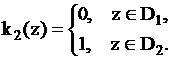
где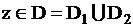 
; 
, 
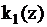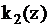– кусочно-постоянные функции, которые можно представить с помощью конечного автомата.
У алфавита этого автомата два выходных символа (они же его состояния)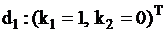 
и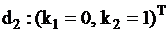 
.
Входными сигналами являются сигналы, говорящие о достижении вектором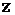 
границ областе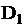й 
и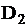 
.
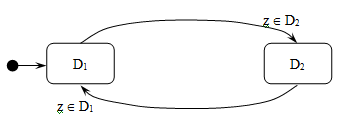
Графическая иллюстрация поведения ГА или карты состояний (statechart) Харела
Состояние 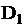помечено как начальное, то есть 
.
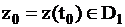В качестве классического примерасистемы, описываемой подобным образом, можно привести динамическую систему, исследуемую в теории управления в задаче об успокоении материальной точки с максимальным быстродействием при наличии ограничений на управление (задача о лифте).
В формализме ГА, дискретная переменная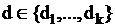 
ставится в соответствие множеству 
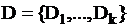узлов графа, называемых основными состояниями (одно из них помечается как начальное).
Одновременно обеспечивается предельно глубокий уровень проникновения в исследуемую предметную область и наиболее высокая степень гибкости и детализация описания системы в рамках разрабатываемой модели.
При реализации дискретного или комбинированного подходов реализуются типовые математические схемы, в которых участвуют как непрерывные переменные, так и дискретные переменные. Выделяют четыре принципиально различающихся подгрупп ЯИМ.
Первая подгруппа ЯИМреализует имитацию путем составления списка событий, отличающих моменты выполнения функциональных операций. Продвижение времени осуществляется по событиям, а про-грамма модели организована в виде совокупности процедур обслуживания событий. Выполнение этих процедур синхронизируется списковым механизмом планирования (расписания) событий. Исходными представителями данной подгруппы являются языки SIMSRIPT, GASP и др.
Вторая подгруппа ЯИМориентирована на просмотр активностей (работ) с целью проверки выполнения условий их начала или окончания. Просмотр активностей осуществляется непрерывно и определяет очередность появления событий. Завершение выполнения активностей может привести к инициализации новых активностей. Языки данного типа имеют в основе поисковый алгоритм и динамика системы описывается в терминах работ. Типопредставителем ЯИМ данной подгруппы является язык FОRSIM.
Третья подгруппа ЯИМреализует процессный способ описания систем. Под процессом понимается последовательность событий, связь между которыми устанавливается логикой определенных отношений. Описание каждого класса процесса оформляется в виде процедуры, которая выполняется одновременно для всех представителей данного класса, существующих в системе в текущее время. Примерами языков процессов является язык SIMULA и язык ПЛИС, которые породили много последующих разработок, используемых в настоящее время
Четвертая подгруппа ЯИМреализует транзактный способ имитации, и ее наиболее известный и широко используемый в настоящее время типопредставитель – язык GPSS (GPSS WORLD, GPSS/PC). Язык моделирования GPSS специально разработан для построения имитационных моделей сложных дискретных систем и представляет собой интерпретирующую языковую систему, применяющуюся для описания пространственно-временного движения объектов. Такие объекты называются транзактами, которые чаще всего являются элементами потока заявок. Функцию каждого из них можно представить как процесс создания, продвижения по системе и уничтожения. Основными схемами, для имитации которых используется язык GPSS, являются, прежде всего, системы массового обслуживания (Q-схемы), автоматы (F, Р-схемы), сети Петри (N-схемы) и даже агрегаты (А-схемы).
К числу современных ЯИМ, реализующих комбинированный (непрерывно-дискретный) подход, может быть отнесен язык Modelica, который реализует принципы объективно-ориентированного программирования применительно к моделированию больших, сложных и физически разнородных систем. Их компоненты могут иметь различную физическую природу. Язык поддерживает имитацию гибридного поведения элементов систем и в настоящее время активно развивается.
Методология SADT.
В рамках методологии SADT разработано несколько графических языков функционального моделирования систем под общей аббревиатурой IDEF (IntegrationDefinitionforFunctionModeling). Из них наибольшее распространение получили нотации IDEF0 и IDEF3.
Для описания работы системы необходимо построить ее модель, дающую адекватное отображение предметной области, всех участников бизнес-процессов организации:
1. как работает организация, деятельность которой собираются автоматизировать?
2. каков состав функциональных подсистем разрабатываемой или модернизируемой системы и как они могут взаимодействовать между собой?
Наиболее удобным языком моделирования в подобных ситуациях является нотация IDEF0.
Первичным является определение контекста – наиболее абстрактного (по сути концептуального) уровня описания системы в целом. Контекст предполагает задание:
1. субъекта область или область моделирования (Scope);
2. целей моделирования (Purpose);
Технология моделирования и проектирования ИС подразумевает сначала создание модели AS-IS, ее анализ и разработку предложений по модернизации всей системы и её отдельных бизнес-процессов, отображаемых в модели ТО-ВЕ. Альтернативные точки зрения отражаются в моделях ForExpositionOnly.
Согласно технологии IDEF0 система представляется в виде совокупности действий (работ) (Activities), которые взаимодействуют между собой на основании правил (Control) с учетом потребляемых информационных, человеческих и производственных ресурсов (Mechanism) и имеют четко определенные вход (Input) и выход (Output).
Работы– обозначаются прямоугольниками и определяют поименованные процессы, функции или задачи, которые происходят в течение определенного времени и имеют распознаваемые результаты.
Взаимодействие работ с внешним миром и между собой описывается в виде стрелок:
cтрелки «Вход (Input)» – материал или информация, которые используются или преобразуются работой для получения результата;
cтрелки «Управление (Control)» – правила, стратегии, процедуры или стандарты, которыми руководствуется работа;
cтрелки «Выход (Output)» – физические объекты или информация, которые производятся работой;
cтрелки «Механизм (Mechanism)» – определяют ресурсы, которые выполняют работу или потребляются при её выполнении.
cтрелки «Вызов (Call)» – специальная стрелка, указывающая на другую модель работы.
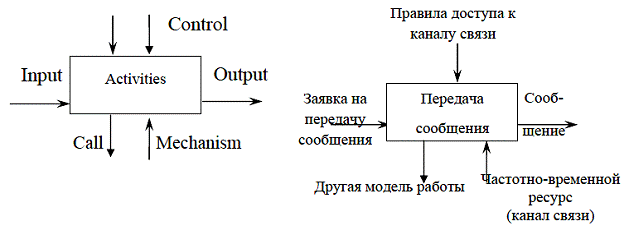
Примеры простых диаграмм IDEF0
Технология ERD.
Диаграммы «сущность-связь» предназначены для графического представления моделей данных разрабатываемой системы и предлагают некоторый набор стандартных обозначений для определения данных и отношений между ними. С помощью этого вида диаграмм описывают компоненты концептуальных моделей данных и
объектов, а также совокупность взаимосвязей между ними, имеющих существенное значение для разрабатываемой информационной системы. Наибольшее использование модели ERD получили при проектировании реляционных баз данных. Нотация ERD была впервые введена П. Ченом (Chen) и получила дальнейшее развитие в работах Баркера. Основными понятиями данной нотации являются понятия сущности и связи.
Сущность (entity)– произвольное множество реальных или абстрактных объектов, каждый из которых обладает своими свойствами и характеристиками. Каждый объект рассматривается как экземпляр одной и только одной сущности, имеет уникальное имя или идентификатор и отличается от других экземпляров данной сущности.
Стандартные графические изображения сущностей
Связь (relationship) –отношение или некоторая ассоциация между отдельными сущностями.
Разделяют связи, реализующие отношения принадлежности или подчиненности типа «отец – сын», «начальник – подчиненный», и связи, реализующие отношения обладания некоторыми свойствами.
Стандартные графические изображения связей
Графическая модель данных строится таким образом, чтобы отражались не только семантический характер описываемого отношения, но и дополнительные аспекты обязательности связи, а также кратности участвующих в данных отношениях сущностей, которые отображаются указанием значений соответствующих переменных.
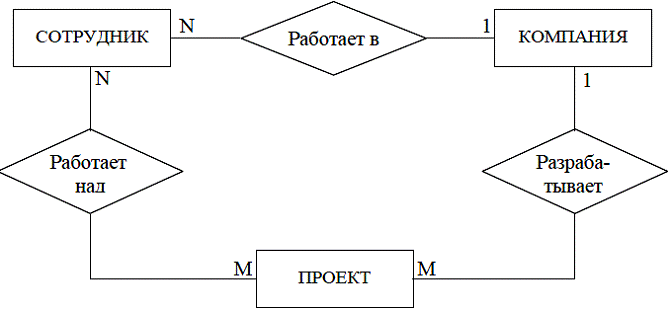
Диаграмма «сущность - связь» для общего примера компании
21.Принципы моделирования системной динамики в Stateflow (1,2,6)
Работа выполняется в среде MATLAB и оформляется в виде m-файла управляющей программы, содержащей обращение к mdl-файлу S-модели с вложенной SF-моделью (SF-диаграммой, SF-машиной) одной из возможных конфигураций СМО. Задания на выполнение работы предполагают проведение исследований различных типов и структур СМО с использованием разнородных показателей для оценки эффективности в зависимости от основных факторов влияния.
Роль УП, как и ранее, состоит в задании варьируемых и неварьируемых факторов, проведении стратегического и тактического планирования модельного эксперимента, реализации процедур статистической обработки результатов моделирования. Роль S-модели заключается в обеспечении динамики процесса функционирования SF-модели и регистрации его результатов на основе использования стандартных элементов подсистемы Simulink. Наконец, роль SF-модели (Stateflow-модели) состоит, собственно, в воспроизведении визуальной модели СМО с использованием формализма гибридных автоматов (карт состояний Харела).
Первоначально при выполнении работы проводится ознакомление с особенностями и возможностями встроенного в подсистему Simulink пакета Stateflow на примере простейших событийно управляемых систем. Далее осуществляется полномасштабная разработка SF-модели в соответствующей оболочке S-модели, в совокупности реализующих моделирование СМО заданного типа. В заключительной части работы осуществляется формирование УП в виде m-файла, реализующего, если это предусматривается заданием, план модельного эксперимента имногократный прогон S-модели с регистрацией результатов для последующей оценки эффективности.При формировании этой программы осуществляется сопряжение с S-моделью и окончательная настройка ее блоков и модулей с учетом выбранных условий моделирования. Однако на начальном этапе удобно разработать упрощенный вариант УП, обеспечивающий предварительное тестирование S-модели с запуском из MATLAB.
Перед началом выполнения работы в соответствующем разделе создается рабочая папка. После запуска MATLAB данная папка устанавливается в окне «CurrentDirectory» путем выбора из списка рабочих папок файловой системы.
Как уже отмечалось, первоначально целесообразно разработать m-файл упрощенного варианта УП, реализующий известные формы обращения к S-модели и задания ее основных параметров.
Далее создается S-модель с вложенной SF-моделью. Для этого осуществляется запуск Simulink и создается пустое окно нового mdl-файла Untitled (впоследствии сохраняемого в различных модификациях под именем testo**.mdl). Осуществляется, как и ранее, установка общих параметров модели ConfigurationParameters, однако теперь в поле Solver группы Solveroptions ц<