Гпсч с источником энтропии или гсч
Наравне с существующей необходимостью генерировать легко воспроизводимые последовательности случайных чисел, также существует необходимость генерировать абсолютно случайные числа. Такие генераторы называются генераторами случайных чисел (ГСЧ — англ. random number generator, RNG). Такие генераторы чаще всего строятся из комбинации ГПСЧ и внешнего источника энтропии (и именно такую комбинацию теперь и принято понимать под ГСЧ). Под источником энтропии понимают некоторые устройства (счетчики) случайных событий.
Почти все крупные производители микрочипов поставляют аппаратные ГСЧ с различными источниками энтропии. Однако на данный момент скорость сбора случайных чисел всеми существующими микрочипами (несколько тысяч бит в секунду) не соответствует быстродействию современных процессоров.
В персональных компьютерах авторы программных ГСЧ используют гораздо более быстрые источники энтропии, такие, как шум звуковой карты или счётчик тактов процессора. Сбор энтропии является наиболее уязвимым местом ГСЧ. Эта проблема до сих пор полностью не разрешена во многих устройствах (например, смарт-картах). Многие ГСЧ используют традиционные испытанные, хотя и медленные, методы сбора энтропии вроде измерения реакции пользователя (движение мыши и т.п.), как, например, в PGP и Yarrow, или взаимодействия между потоками, как, например, в Java secure random.
Пример простейшего ГСЧ с источником энтропии
Если в качестве источника энтропии использовать текущее время, то для получения натурального числа от 0 до N достаточно вычислить остаток от деления текущего времени в миллисекундах на число N+1. Недостатком этого ГСЧ является то, что в течение одной миллисекунды он выдает одно и то же число.
Примеры ГСЧ и источников энтропии приведены в таблице 3.1
Таблица 3.1. – ГСЧ и источники энтропии
| Источник ГСП | Источник энтропии | ГПСЧ |
| /dev/random в UNIX/Linux | Счётчик тактов процессора | LFSR, с хешированием выхода через SHA-1 |
| Yarrow от Брюса Шнайера | Традиционные методы | AES-256 и SHA-1 маленького внутреннего состояния |
| Microsoft CryptoAPI | Текущее время, размер жёсткого диска, размер свободной памяти, номер процесса и NETBIOS-имя компьютера | MD5-хеш внутреннего состояния размером в 128 бит |
| Java SecureRandom | Взаимодействие между потоками | SHA-1-хеш внутреннего состояния (1024 бит) |
| Chaos от Ruptor | Счётчик тактов процессора | Хеширование 4096-битового внутреннего состояния на основе нелинейного варианта Marsaglia-генератора |
| RRAND от Ruptor [5] | Счётчик тактов процессора | Зашифровывание внутреннего состояния поточным шифром EnRUPT в authenticated encryption режиме (aeRUPT) |
На основе ГСЧ, генерирующего последовательность случайных чисел, имеющую равномерное распределение, алгоритмическими методами легко создаются UCX с различными законами распределения.
Различные вероятностные распределение алгоритмически моделируются следующими способами:
1) с показательным законом распределения:
 , где
, где 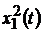 и
и 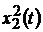 – гауссовские случайные процессы с нулевым средним и единичной дисперсией;
– гауссовские случайные процессы с нулевым средним и единичной дисперсией;
2) с нормальным (гаусовским) законом распределения:
 , где
, где 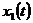 и
и  – случайные процессы с равномерным распределением в диапазоне [0,1];
– случайные процессы с равномерным распределением в диапазоне [0,1];
3) с рэлеевским законом распределения:
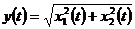 , где
, где 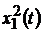 и
и 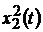 – гауссовские случайные процессы с нулевым средним и единичной дисперсией;
– гауссовские случайные процессы с нулевым средним и единичной дисперсией;
4) с распределением Вейбулла:
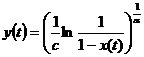 , где
, где 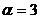 ,
,  и
и 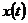 – случайный процесс с равномерным распределением в диапазоне [0,1].
– случайный процесс с равномерным распределением в диапазоне [0,1].
Порядок выполнения:
1. Выполнить имитацию вероятностных распределений четырех видов согласно варианта, используя ГСЧ с равномерным распределением в диапазоне [0, 1].
а) построить временные ряды;
б) произвести анализ статистических характеристик случайных процессов (найти математическое ожидание и дисперсию сигналов);
2. Выполнить имитацию смеси трех сигналов:
а) периодический сигнал необходимо сложить с первым случайным сигналом согласно варианта;
б) периодический сигнал необходимо сложить со вторым случайным сигналом согласно варианта;
в) периодический сигнал необходимо сложить с третьим случайным сигналом согласно варианта;
г) сложить все четыре случайных сигнала согласно варианта;
д) найти математическое ожидание сигнала для случаев (а) – (г);
е) найти дисперсию общего для случаев (а) – (г);
3. Вывести временные ряды полученных сигналов в виде графиков и табличных массивов данных.
Варианты заданий
| Ва- ри- ант | Виды законов распределений случайных сигналов | ||||
| Показа- тельный | Нормальный | Рэлеев- ский | Вейбула | Периодический сигнал | |
| + | +, m=2;s=1 | – | + | синусоидальный | |
| + | +, m=0;s=2 | + | – | косинусоидальный | |
| – | +, m=5;s=4 | + | + | ступеньчатый | |
| +, m=3;s=2,5 | – | П-образный | |||
| + | +, m=7;s=3 | + | – | из равносторонних треугольников, имеющих общую точку соприкосновения | |
| + | +, m=10;s=7 | – | + | из полукругов | |
| + | +, m=4;s=3 | + | – | пила в виде прямоугольных трапеций | |
| + | +, m=0;s=3 | – | + | пила в виде прямоугольных треугольников с гипотенузой справа | |
| – | +, m=5;s=7 | + | + | пила из парабол и прямых линий | |
| – | +, m=2,5;s=2 | + | + | сигнал из косинусоиды по модулю | |
| – | +, m=2;s=1,8 | + | + | сигнал из равнобедренных треугольников, перекрывающих друг друга (холмы) | |
| + | +, m=3;s=1,5 | – | + | пила в виде прямоугольных треугольников с гипотенузой слева | |
| + | +, m=0;s=3 | + | – | сигнал “хоккейная клюшка” | |
| – | +, m=5;s=4 | + | + | сигнал в виде отдельных отрезков под углом 45° (слеш) | |
| + | +, m=3;s=2,8 | + | – | S-образный сигнал | |
| – | +, m=0;s=5 | + | + | Сигнал из накладывающихся друг на друга перевернутых восьмерок | |
| + | +, m=7;s=4,5 | – | + | сигнал из равнобедренных трапеций | |
| + | +, m=0;s=5 | + | – | X-образный сигнал (сигнал “ромбики”) | |
| – | +, m=7;s=3 | + | + | Сигнал растянутой спирали | |
| + | +, m=2;s=1 | – | + | Сигнал “перекрывающиеся кольца” | |
Контрольные вопросы:
1. Какими способами можно получить случайный процесс с экспоненциальным распределением?
2. Какими способами можно получить случайный процесс с рэлеевским распределением?
3. Как можно оценить математическое ожидание и дисперсию случайной величины по соответствующим графикам плотности распределения вероятностей?
4. Какова связь между средним квадратом и дисперсией случайной величины?
5. Каким образом можно найти математическое ожидание случайной величины, зная её плотность распределения вероятностей?
6. Каким образом можно найти средний квадрат случайной величины, зная её плотность распределения вероятностей?
7. Как определить по графику плотности распределения вероятностей вероятность попадания случайной величины в заданный промежуток её значений?
8. Какие реальные случайные процессы имеют нормальное (гауссово) распределение, рэлеевское распределение, равномерное распределение, распределение Пуассона?
9. Каковы основные характеристики генератора случайных чисел в ЭВМ: закон распределения, интервал изменения случайных чисел?
10. В чем заключается центральная предельная теорема теории вероятностей?
11. Каковы характерные особенности модели белого шума?
1.2 Рекомендуемая литература
1. Е.И. Гурский Теория вероятностей с элементами математической статистики: уч. пос. для вузов / Е.И. Гурский. – М.: Вс. шк., 1971. – 328 с.
2. Дж. Купер. Вероятностные методы анализа сигналов и систем / Дж. Купер, К. Макгиллем; пер. с англ. В.Т. Горяинова. – М.: Мир, 1989. – 376 с.
3. В.П. Бакалов. Цифровое моделирование случайных процессов / В.П. Бакалов. – М.: Сайнс-пресс, 2002. – 88 с. – (Серия «Конспекты лекций по радиотехническим дисциплинам» ; вып. 4).
4. Боровиков В. STATISTICA для профессионалов. СПб.: Питер. 2001. – 655 с.
5. Гультяев А.К. Matlab 5.2. Имитационное моделирование в среде Windows: практическое пособие.
Лабораторная работа №4
