Графический метод нахождения смешанных стратегий, сведение матричной игры к задаче линейного программирования.

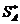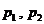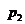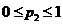Решению из предыдущего раздела можно придать естественную графическую форму. Итак, вначале мы были заняты поиском оптимальной смешанной стратегии нападающего. Она задаётся двумя неотрицательными числами – частотами. Но поскольку их сумма равняется единице, смешанную стратегию можно, по существу, задать одним числом , где . Будем откладывать переменную 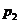по оси абсцисс, а по оси ординат будем откладывать средние выигрыши нападающего. Мы нарисуем два графика: средние выигрыши в случае, когда вратарь применяет чистую стратегию 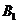и в случае, когда он применяет чистую 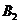. При этом мы будем использовать тот общий факт, что такие зависимости линейные; и то, что две точки 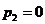– при и при 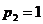− непосредственно «считываются» из таблицы (12.1) (первая из них соответствует чистой стратегии 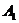нападающего, а вторая – чистой стратегии 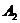). Получаем следующую картинку:

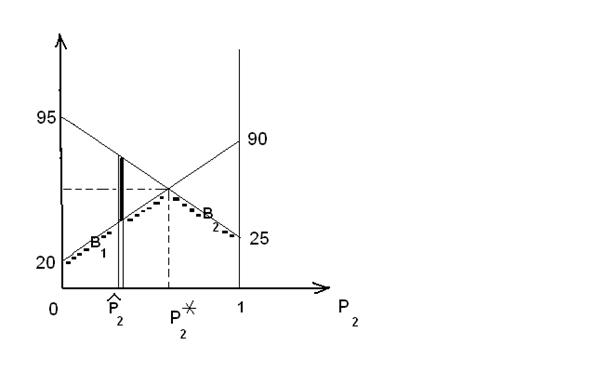
Теперь порассуждаем, глядя на неё. Как и выше, будем «болеть» сначала за команду нападающего, т.е. за игрока A. Нам надо помочь ему выбрать оптимальную смешанную стратегию. Теперь, вместо развилки трёх «дорог» из раздела 11, мы имеем бесконечное количество «дорог», индексированных вещественными числами 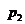от 0 до 1. Предположим, что мы выбрали «дорогу» с некоторым значением 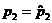. Что самое худшее нас ждёт на ней? Проведём на картинке вертикальную двойную линию, соответствующую 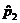. Ордината точки её пересечения с прямой, отвечающей стратегии 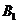вратаря, является средним выигрышем форварда при условии, что вратарь применяет чистую 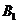. Тоже верно и для точки пересечения со второй прямой, соответствующей 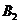. А что будет, если вратарь решит применить различные смешанные стратегии? Нетрудно сообразить, что соответствующие средние выигрыши нападающего заполнят «жирный» вертикальный отрезок между двумя рассмотренными только что точками. Из рисунка видно, что самый худший для нас вариант – это чистая стратегия 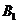. Отметим соответствующую точку дополнительно маленьким прямоугольником. Пусть теперь значение 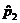«пробежит» от 0 до 1. Тогда отмеченные точки образуют так называемую нижнюю огибающую двух наших прямолинейных графиков: в данном случае, это будет отмеченная прямоугольниками «крышечка». Выбираем теперь такое значение 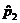, при котором наихудший вариант будет относительно наилучшим – вновь применяем принцип максимина (как в разделе 11). Точка максимума огибающей – в данном случае точка пересечения прямых – и даст искомое оптимальное значение 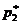. Разумеется, значение 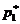находится по формуле 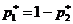. Тем самым, оптимальная смешанная стратегия нападающего 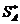найдена.

Теперь «поболеем» за команду, которую представляет вратарь B. Аналогичным образом мы получим следующую картинку

Как и выше, рассматриваем фиксированную смешанную стратегию вратаря, соответствующую значению . Возможные средние выигрыши нападающего (т.е. проигрыши вратаря) заполнят вновь «жирный» отрезок. Однако в данном случае самым худшим для нас (т.е. для вратаря) будет наибольшее значение ординаты. Таким образом, надо рассматривать верхнюю огибающую прямых, отмеченную на рисунке маленькими пустыми прямоугольниками. Поскольку мы стремимся минимизировать наш проигрыш, мы выбираем значение , соответствующее минимуму огибающей – точке пересечения прямых в данном случае (принцип минимакса). Вычисляя 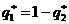, мы определяем оптимальную смешанную стратегию 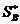вратаря.

Аналогичный графический метод решения применим для игр, описываемых матрицами размера 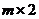или 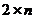. В этих случаях надо начинать графическое решение обязательно с игрока с двумя стратегиями (т.к. именно его смешанная стратегия определяется ровно одним параметром). Рассмотрим, например, матричную игру 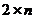. В этом случае всевозможные смешанные стратегии игрока A определяются значением 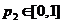. Для каждой чистой стратегии игрока B мы получаем, как и выше, график среднего выигрыша игрока A – некоторый прямолинейный отрезок. Только теперь их будет 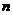штук. Рассуждая как выше, приходим к построению нижней огибающей этих 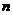графиков и нахождению её максимума (принцип максимина). Абсцисса точки максимума и будет искомым значением .

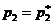Однако для нахождения оптимальной стратегии игрока B (при 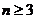)нарисовать графики не удастся, т.к. эта стратегия определяется уже 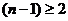параметрами. Рассмотрим, тем не менее, практически общую ситуацию, когда точка максимума нижней огибающей графиков для игрока A определяется точкой пересечения ровно двух прямых, как на следующем чертеже:

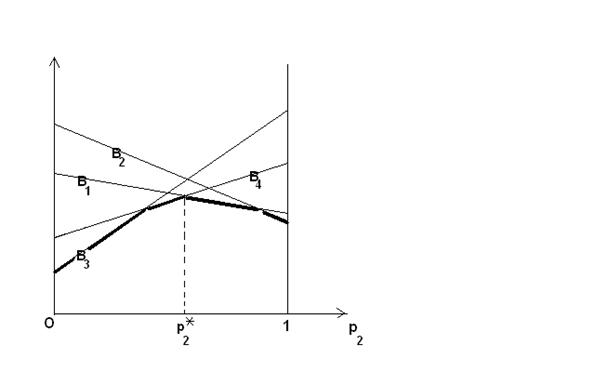
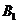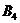Из рисунка видно, что точка максимума порождена пересечениями прямых, отвечающих стратегиям и игрока B . А отсюда следует, что игрок B в ответ на оптимальную смешанную стратегию 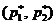должен применить некоторую смешанную стратегию, в которой активными являются лишь стратеги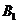и и 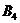(т.е про остальные две он вообще должен забыть). Тем самым, задача свелась к игре 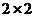, рассмотренной выше, и мы графически сможем определить частоты стратеги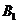й и 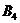в оптимальной смешанной стратегии (остальные частоты будут нулевыми).

Что же делать в случае произвольной матричной игры 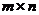? Во-первых, необходимо попробовать свести её к задачам меньших размеров (например, рассмотренным выше) с помощью принципа доминирования строк или столбцов. Предположим, что в платёжной матрице для 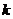-й и 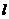-й строк выполняется соотношение 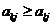для всех 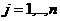. Это означает, что при любой чистой стратегии 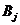игрока B игроку A выгодней применять стратегию 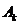по сравнению со стратегией 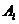. Тем самым, он может просто забыть про стратегию 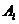и вычеркнуть её из платёжной матрицы. Тем самым, мы придём к игре меньшего размера: 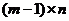. Аналогично, если для 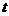-го и 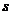-го столбцов платёжной матрицы выполняются неравенства 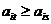для всех 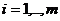, то игроку B всегда выгодней применять стратегию 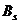по сравнению со стратегией 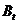какую бы стратегию ни использовал игрок A (обратите внимание на различие, связанное с тем, что элементы платёжной матрицы – это проигрыши игрока B). Итак, в этом случае игрок B может вычеркнуть свою стратегию 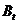и игра сведётся к игре размера .

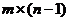Наконец, если даже после этого мы имеем игру 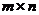, где оба размера не меньше 3, мы сводим задачу к задаче линейного программирования следующим образом.

«Поболеем» вначале за игрока A. Мы вновь на развилке «дорог», каждая из который на этот раз определяется набором из 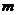неотрицательных чисел 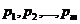с условием 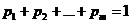. Фиксируем одну из них. Если наш оппонент B применит одну из своих чистых стратегий 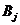( 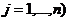, то наш средний выигрыш будет составлять 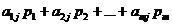. Ясно, что если B будет применять смесь стратегий 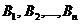с частотами 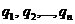, то наш средний выигрыш будет равняться линейной комбинации указанных выше 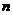чисел с этими коэффициентами. Что же самое худшее ждёт нас? Разумеется, минимум из этих 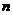чисел (так как сумма коэффициентов 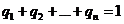). Теперь нам надо найти тот набор 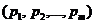, сумма которого равна 1, для которого этот минимум максимален (вновь принцип максимина). Далее делается неожиданный ход: минимум из рассматриваемых 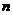чисел можно, очевидно, найти как наибольшее число 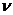такое, что выполняется система неравенств:

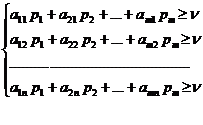(13.1)

А далее из этих максимальных значений 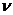нам надо выбрать самое максимальное при различных наборах 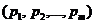. Будем считать для удобства, что с самого начала все значения 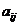положительны (этого легко добиться, прибавляя ко всем выигрышам одно и тоже число, что не изменит относительного соотношения выгодности между стратегиями). Тогда максимальное 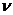для системы (13.1) будет также положительным, и мы можем ввести новые переменные, принимающие неотрицательные значения:

.

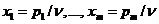В новых переменных система (13.1) будет иметь вид

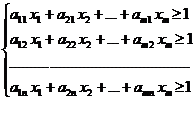(13.2)

При этом имеем 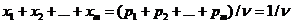. Значение 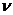мы хотим сделать наибольшим; следовательно, надо подбирать такие 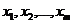, удовлетворяющие системе (13.2), чтобы выражение 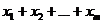принимало наименьшее значение:

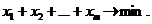(13.3)

При этом частоты 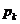выражаются через 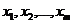однозначно:

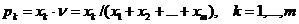. (13.4)

Итак, нахождение оптимальной смешанной стратегии свелось к решению задачи линейного программирования (13.2)-(13.3) и последующему вычислению частот по формуле (13.4).

Рассуждая аналогично для игрока B, мы рассмотрим его смешанную стратегию 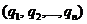как одну из «дорог» и заметим, что наихудшей ситуацией на этой «дороге» будет проигрыш в размере максимума из чисел 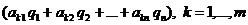. Этот максимум есть наименьшее решение 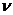системы неравенств

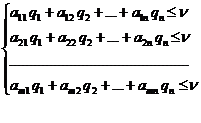
Вводя переменные

,

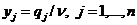приходим к системе

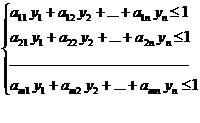(13.5)

и условию

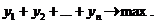(13.6)

При этом

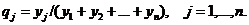(13.7)

Итак, задача нахождения оптимальной смешанной стратеги игрока B свелась к задаче линейного программирования (13.5)-(13.6) и последующему вычислению частот 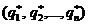по формуле (13.7).

Интересно отметить, что задачи линейного программирования (13.2)-(13.3) и (13.5)-(13.6) являются взаимно-двойственными; а стало быть, достаточно решить симплекс-методом только одну из них и решение другой получится автоматически по теоремам двойственности.

Раздел 14