Основные виды теоретических распределений

Равномерное (прямоугольное) распределение.Случайная вели­чина X имеет равномерное распределение на участке от а до b, если ее плотность f(x) на этом участке постоянна (рис.1.9,а):

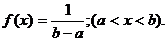(1.33)

Функция распределения F(x) равномерно распределенной случай­ной величины X геометрически представляет собой площадь, ограниченную кривой распределения и лежащую левее точки х (рис.1.9,б):

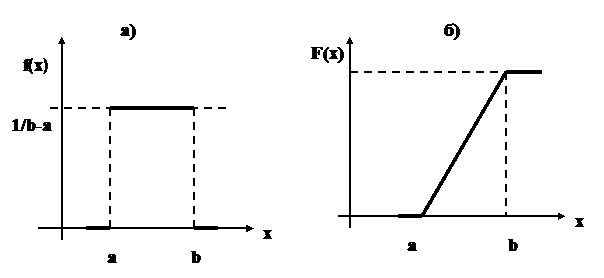
Рис. 1.9. Равномерное распределение

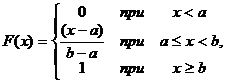(1.34)

Любой точке в интервале (0, 1) соответствует одна и та же вероятность. Математическое ожидание (среднее значение) и дис­персия равны соответственно

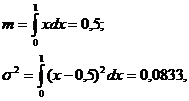(1.35)

а стандартное отклонение (среднее квадратическое отклонение от математического ожидания) σ =0,2887. Примерно 57,74% всех случайных реализаций равномерно распределенных случайных величин располагаются в пределах ± σ.

Типичным представителем равномерно распределенных слу­чайных чисел (РРСЧ) являются числа рулетки. В природе, по-ви­димому, не существует явлений с равновероятным распреде­лением. При математическом моделировании систем РРСЧ ис­пользуют весьма широко в качестве генераторов событий и ис­ходных данных для получения случайных чисел, распределенных по тому или иному закону. Во второй части пособия представ­лены генераторы РРСЧ и способы их преобразования к задан­ному закону распределения.

Для равномерно распределенных двух независимых случай­ных величин плотность распределения и функция распределения записываются по правилам умножения соответственно в виде:

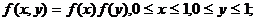(1.36)

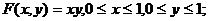(1.37)

Из этих выражений следует, что одна и та же вероятность соответствует лю­бой точке внутри квадрата (рис.1.10) с вершинами 0,0; 1,0; 1,1; 0,1. Матема­тическое ожидание и дисперсия такого распределения равны

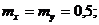(1.38)

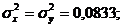(1.39)

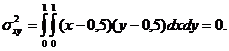(1.40)

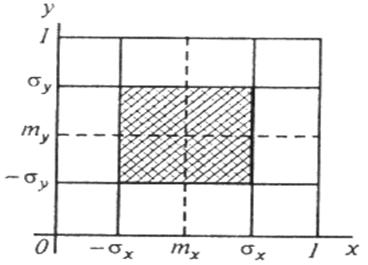
Рис. 1.10. Двумерная плот­ность равномерного рас­пределения

Стандартные отклонения имеют значение σ_х=σ_у=0,2887 и примерно треть всех реализаций, как это показано с помощью заштрихованной области на рис. 1.10, заключено в пределах ±σ_х и ±σ_у. Таким же образом находят математическое ожидание и все остальные моменты для любого числа случайных перемен­ных величин, независимых и равномерно распределенных. При совместном изменении нескольких случайных величин в интерва­ле от нуля до единицы значения математического ожидания, дисперсии, третьего и четвертого моментов для каждой из них те же, что и для одной случайной величины.

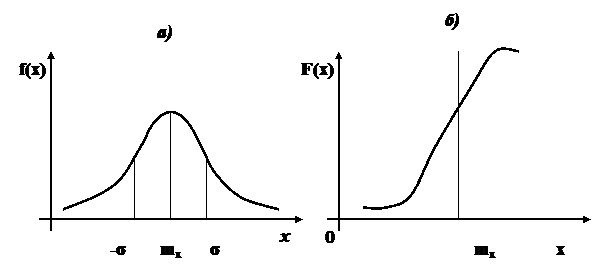
Рис. 1.11. Нормальное распределение

Нормальное распределение. Нормальный закон распределения (распределение Гаусса) занимает среди других законов особое положение, с ним связано большинство задач, решаемых в науч­ной и инженерной практике.

Случайная величина X распределена по нормальному закону с математическим ожиданием т и дисперсией σ², если ее плот­ность распределения (рис.1.11,а) и функция распределения (рис.1.11,б) имеют вид:

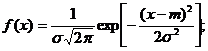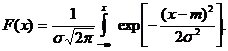(1.41)   (1.42)

На рис.1.12 показаны три кривые плотности нормальных распределений; для всех трех m = 0; для кривой 1 σ = 1; для кривой 2 σ = 2,5; для кривой 3 σ = 0,5.

Правило «трех сигм».Если случайная величина распределена нормально, то ее отклонение от математического ожидания прак­тически (с вероятностью 0,9973) не превышает 3σ. На практике это правило иногда используют для отбраковки данных, а также для грубой оценки возможности отнесения закона распределения к нормальному:

• объекты выборки, характеристики которых отклоняются от среднего значения более чем на три стандарта, исключают из состава этой выборки;

• если распределение изучаемой случайной величины неиз­вестно, но абсолютная величина отклонения любого объекта выборки от среднего значения не превышает трех стандартов, тогда есть основание полагать, что изучаемая величина распределена нормально.

Распределение Стьюдента.Распределением Стьюдента (псев­доним английского статистика В. Госсета) называют отношение нормально распределенной случайной величины у к квадратному корню из среднего значения квадратов случайных величин y_i с те­ми же параметрами распределения (рис.1.13), т. е. это распределе­ние для величины 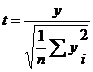с плотностью с разными дисперсиями

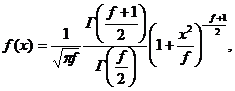(1.43)

при 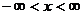; Г (f) - гамма-функция. Параметр f называют числом степеней свободы. Этот параметр равен n-1, где п - объем выборки. В таблицах распределения Стьюдента обыч­но приводят значения интегральной функции распределения и квантили этого распределения в пределах от - ∞ до х. Переход к другим условиям не представляет затруднений.

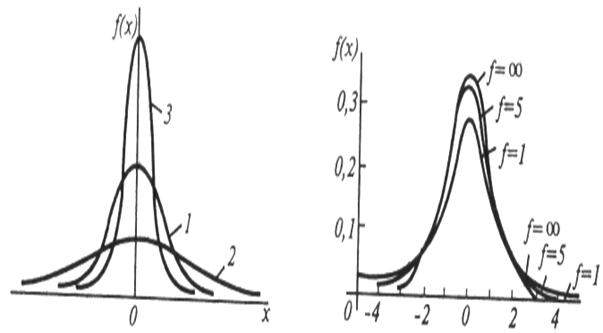
Рис.112. Нормальные распределения Рис.1.13. Распределение Стьюдента

С возрастанием числа степеней свободы распределение Стью­дента быстро приближается к нормальному.

Распределение χ-квадрат.Пусть X_i есть нормальные независи­мые случайные величины, причем математическое ожидание каж­дой из них равно нулю, а среднее квадратическое отклонение — единице. Тогда сумма квадратов этих величин 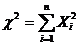распределена по закону χ² (читается «хи-квадрат») с f=n степеня­ми свободы (рис. 1.14); если же эти величины связаны одним линейным соотношением, например 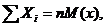, то число степе­ней свободы f= п — 1.

С увеличением числа степеней свободы распределение хи-ква­драт медленно приближается к нормальному.

Для функций 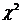имеются таблицы, которые используют для проверки согласия статистических данных.

Показательное распределение.Показательное или экспоненци­альное распределение имеет плотность (рис.1.15)

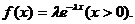(1.44)

Положительную величину λ называют параметром показа­тельного распределения.

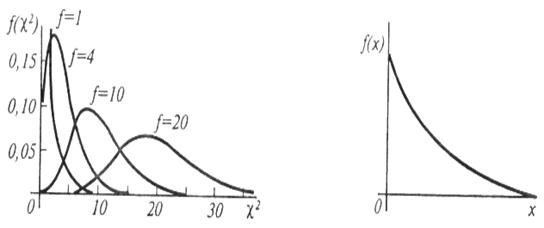
Рис.1.14.Распределение -квадрат Рис.1.15. Показательное распределение

Рис. 1.16. Распределение Гумбеля Рис. 1.17. Распределение Вейбулла

Математическое ожидание и среднее квадратичное отклоне­ние случайной величины, имеющей показательное распределение, обратно его параметру λ:

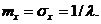(1.45)

Показательное распределение тесно связано с интервалом времени между двумя соседними событиями в стационарном потоке событий. Оно играет большую роль в теории массового обслуживания, в теории надежности и др.

Распределение Гумбеля.Плотность распределения Гумбеля или двойного экспоненциального распределения (рис. 1.16) выража­ется формулой

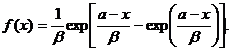(1.46)

Это распределение часто используется для описания снеговых нагрузок на сооружения.

Распределение Вейбулла.Распределение Вейбулла (рис. 1.17) описывает явления, связанные с задачами долговечности и уста­лости, в теории хрупкого разрушения материалов и др. Плот­ность распределения имеет вид

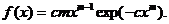(1.47)