Проверка адекватности модели.

Адекватность модели оценивается проверкой выполнения условий:1) случайности;2) независимости последовательных уровней (отсутствием автокорреляции) и 3) нормальности распределения ряда остатковε(t).

1. Проверку случайности уровней остаточной компоненты проводим на основе критерия поворотных точек. Для этого каждый уровень ряда ε(t) сравниваем с двумя соседними.Общее число поворотных точек равно p=6.Рассчитаем значение q. Имеем для n=16

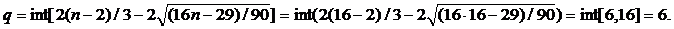p=6, q=6, условие случайности уровней ряда остатков выполнено.

2.Проверка некоррелированности остатков может быть проведена двумя способами и включать два этапа.

2а. Проверка по d-критерию дает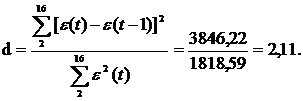

Имеем 4-2,11=1,89 (d₁=1.10; d₂=1,37). 1,37<1,89<2, тогда уровни ряда остатков являются независимыми.

2б.Проверка по первому коэффициенту автокорреляции r(1):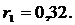

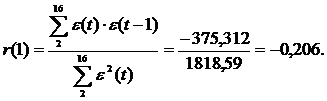
Так как 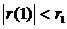, т.е. 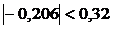, то уровни ряда остатков независимы.

3. Проверка соответствия ряда остатков нормальному распределению (определяем по RS-критерию). Рассчитаем ,при n=16

, ,

, .

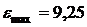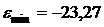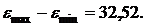
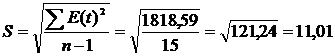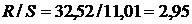Все условия адекватности и точности выполнены. Можно говорить об удовлетворительном качестве модели и возможности проведения прогноза показателя 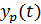на четыре квартала вперед.

5). Расчет прогнозных значений.

Составим прогноз на четыре квартала вперед (т.е. на 1 год с t=17 по t=20). Максимальное значение t, для которого могут быть рассчитаны коэффициенты a₀(t), a₁(t) определяется количеством исходных данных и равно 16. Определим прогнозные значения экономического показателя y_р(t), для t=17,18,19,20.

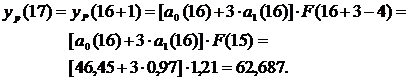
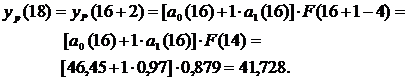
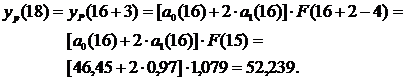
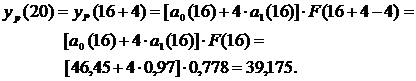
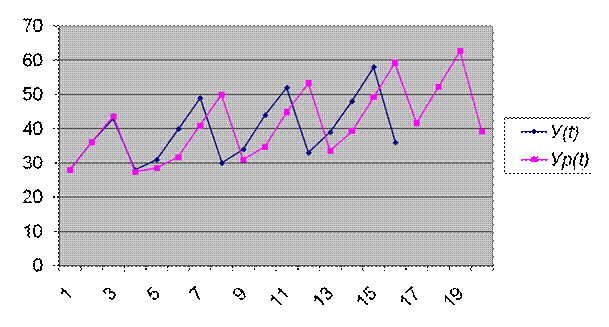
На графике видно, что расчетные данные хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

Эконометрические исследования

Статистического ряда

Задача.По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (y, млн. руб.) от объема капиталовложений (x, млн. руб.).Данные для расчетов представлены в таблице.

xi
yi

Цель.

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 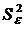; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента ( ).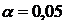

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера ( 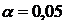), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя y при уровне значимости 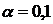, если прогнозное значение фактора x составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

∙ гиперболической;

∙ степенной;

∙ показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод о качестве моделей.

Решение.