Точечный и интервальный прогноз

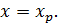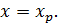Для расчета доверительного интервала прогноза необходимо определить среднюю ошибку положения линии регрессии при заданном значении Другими словами, необходимо определить стандартную ошибку, предсказываемого по линии регрессии среднего значения экономического результата, при заданном значении Из предположения о независимости ошибок 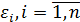и следует независимость случайной величины 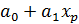(которая зависит только от 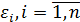) и случайной величины 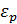(которая не зависит от 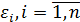в силу предпосылок МНК о случайности остатков). Тогда 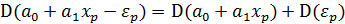–по правилу сложения дисперсий независимых случайных величин.

В уравнении регрессии 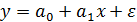проведем усреднение и выделим параметр 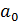: 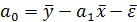. Последнее слагаемое равно 0 в силупредпосылок МНК. Теперь перепишем уравнение регрессии в виде:

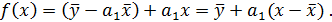
Отсюда, 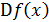зависит от дисперсии ошибки среднего значения величины , определенной при участии 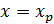и дисперсии коэффициента 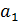. Имеем

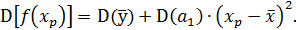
Поскольку суммы теоретических (генеральных) и выборочных значений результативного признака совпадают, т.е. 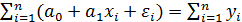, то совпадают и средние значения этих рядов 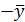. Отсюда следует выражение для дисперсии первого слагаемого 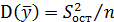. Дисперсия коэффициента регрессии 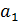, как уже было показано, дается формулой .

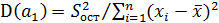Таким образом, формула для расчета стандартной дисперсии ошибки, предсказываемого по линии регрессии значения, имеет вид

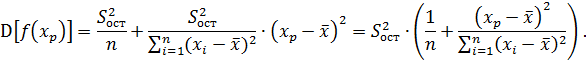
Отсюда, ошибка положения лини регрессии при 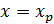, дается формулой

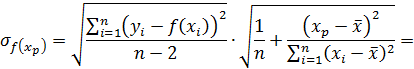
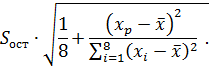
Вычисленное значение позволяет сделать вывод, что в генеральной совокупности линия регрессии для фактора окажется в интервале

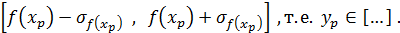
Очевидно, что величина стандартной ошибки 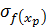будет минимальной, если 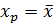и она будет возрастать при отклонении от . Таким образом, ошибка будет малой, если признак-фактор находится где-то вблизи центра корреляционного облака.

Если необходимо с некоторой вероятностью сделать прогноз расчетного значения 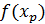,по уравнению регрессии имея в виду уже генеральную совокупность статистических данных, то доверительный интервал дается выражением

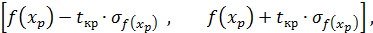
т.е.

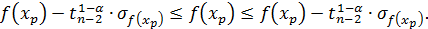
Пусть 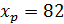, тогда .

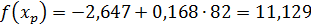Для интервального прогноза индивидуального значения (а не только одной линии регрессии, в целом, как прежде), найдем среднюю стандартную ошибку предсказываемого значения объема продаж. Она вычисляется как корень квадратный из суммы квадрата ошибки положения линии регрессии 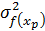и остаточной (необъясненной) дисперсии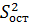

.

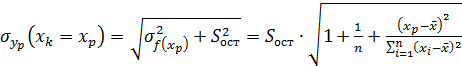Индивидуальные значения y могут отклоняться от 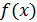на величину случайной ошибки ε, рассчитываемой по остаточной дисперсии 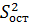на одну степень свободы. Поэтому ошибка, предсказываемого отдельного значения, должна включать не только стандартную ошибку 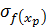, которая характеризует положение линии регрессии, но и случайную ошибку 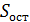(это добавляет 1-цу под знак корня).

Для индивидуального значения прогноза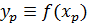

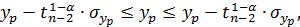
где величина 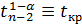представляет собой табличное значение t-критерия Стьюдента на уровне значимости α при числе степеней свободы n–2.

Напомним, что доверительным интервалом называется такой интервал, для которого с наперед заданной вероятностью можно утверждать, что прогнозируемый показатель не выйдет за его пределы. Ширина интервала зависит от качества модели и выбранной вероятности.

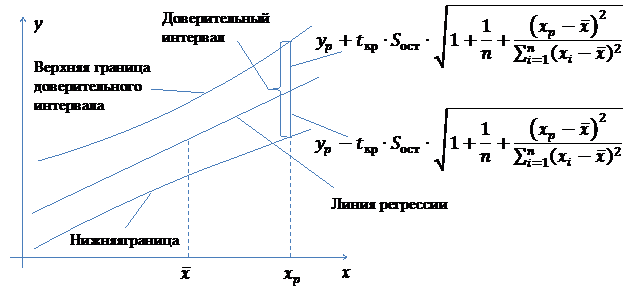
К интервальному оцениванию прибегают при малых выборках, когда точечные оценки не являются устойчивыми. Объем выборки 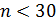берется за основу, когда невозможно организовать сплошное наблюдение генеральной совокупности. Главная проблема эконометрического анализа, связанная с малой выборкой состоит в том, что случайные ошибки, измеряемой характеристики, подчиняются не гауссовскому закону распределения, а закону Стьюдента. В то время как распределение ошибок, исследуемой характеристики в генеральной совокупности, подчиняется гауссовскому закону или близкому к нему.

С точки зрения исходных статистических данных и уравнения регрессии качество модели определяется двумя показателями: адекватностью и точностью.

В общем случае различают два вида статистического прогнозирования: 1) факторное прогнозирование, основанное на количественном измерении параметров регрессии, в частности, коэффициента корреляции, значение которого предполагается неизменным; 2) авторегрессионное прогнозирование – по тренду и цикличности. К настоящему моменту мы рассматриваем – первое.

Вопросы для обсуждения

1. Объясните, чем вызвано появление в модели парной регрессии случайной переменной ε ?

2. Почему перед построением модели парной линейной регрессии необходимо рассчитывать коэффициент корреляции?

3. Объясните смысл понятия «число степеней свободы».

4. По каким вычислениям можно судить о значимости модели в целом?

5. Зачем необходимо рассчитывать t-критерий Стьюдента?

6. Зачем необходимо оценивать интервалы прогноза по линейному уравнению регрессии?

7. В каких пределах должна находиться ошибка аппроксимации, чтобы можно было сделать вывод о хорошем подборе модели к исходным данным?

8. В чем суть предсказания индивидуальных значений зависимой переменной?

9. В каких пределах находится коэффициент детерминации?

10. С увеличением объема выборки: а) увеличивается точность оценок; б) уменьшается ошибка регрессии; в) расширяются интервальные оценки; г) уменьшается коэффициент детерминации; д) увеличивается точность прогноза по модели. (Да; нет; не определено.Ответ поясните).